
3、设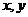 是满足
是满足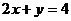 的正数,则
的正数,则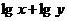 的最大值是
▲
.
的最大值是
▲
.
2、不等式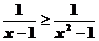 的解集为
▲
的解集为
▲
1、已知集合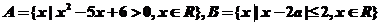 ,若
,若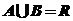 ,则实数
,则实数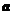 的取值范围是______▲_____.
的取值范围是______▲_____.
2.复合函数单调性的判断
对于函数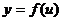 和
和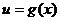 ,如果
,如果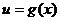 在区间
在区间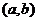 上是具有单调性,当
上是具有单调性,当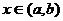 时,
时,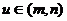 ,且
,且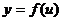 在区间
在区间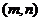 上也具有单调性,则复合函数
上也具有单调性,则复合函数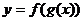 在区间
在区间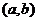 具有单调性的规律见下表:
具有单调性的规律见下表:
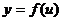 |
增 ↗ |
减 ↘ |
||
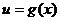 |
增 ↗ |
减 ↘ |
增 ↗ |
减 ↘ |
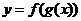 |
增 ↗ |
减 ↘ |
减 ↘ |
增 ↗ |
以上规律还可总结为:“同向得增,异向得减”或“同增异减”.
证明:①设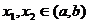 ,且
,且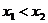
∵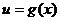 在
在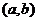 上是增函数,
上是增函数,
∴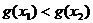 ,且
,且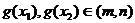
∵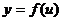 在
在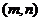 上是增函数,∴
上是增函数,∴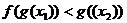 .
.
所以复合函数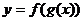 在区间
在区间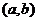 上是增函数
上是增函数
②设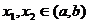 ,且
,且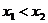 ,∵
,∵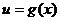 在
在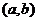 上是增函数,
上是增函数,
∴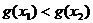 ,且
,且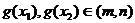
∵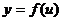 在
在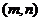 上是减函数,∴
上是减函数,∴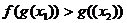 .
.
所以复合函数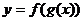 在区间
在区间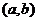 上是减函数
上是减函数
③设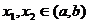 ,且
,且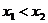 ,∵
,∵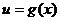 在
在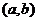 上是减函数,
上是减函数,
∴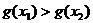 ,且
,且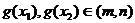
∵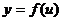 在
在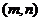 上是增函数,∴
上是增函数,∴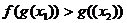 .
.
所以复合函数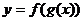 在区间
在区间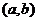 上是减函数
上是减函数
④设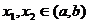 ,且
,且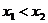 ,∵
,∵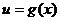 在
在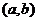 上是减函数,
上是减函数,
∴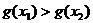 ,且
,且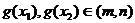
∵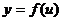 在
在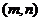 上是减函数,∴
上是减函数,∴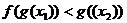 .
.
所以复合函数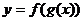 在区间
在区间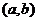 上是增函数
上是增函数
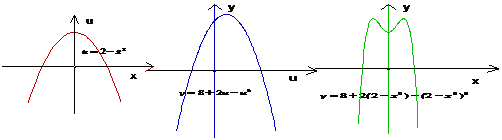
例2.求函数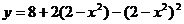 的值域,并写出其单调区间
的值域,并写出其单调区间
解:题设函数由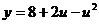 和
和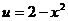 复合而成的复合函数,
复合而成的复合函数,
函数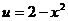 的值域是
的值域是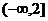 ,
,
在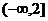 上
上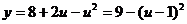 的值域是
的值域是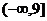 .
.
故函数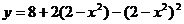 的值域是
的值域是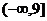 .
.
对于函数的单调性,不难知二次函数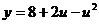 在区间
在区间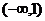 上是减函数,在区间
上是减函数,在区间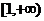 上是增函数;
上是增函数;
二次函数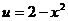 区间
区间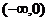 上是减函数,在区间
上是减函数,在区间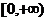 上是增函数
上是增函数
当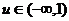 时,
时,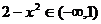 ,即
,即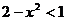 ,
,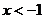 或
或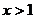 .
.
 当
当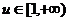 时,
时,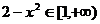 ,即
,即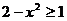 ,
,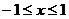 .
.
因此,本题应在四个区间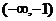 ,
,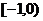 ,
,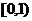 ,
,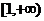 上考虑
上考虑
① 当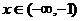 时,
时,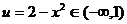 ,
,
而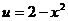 在
在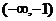 上是增函数,
上是增函数,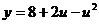 在
在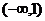 上是增函数,所以,函数
上是增函数,所以,函数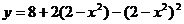 在区间
在区间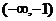 上是增函数
上是增函数
②当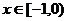 时,
时,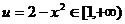 ,
,
而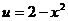 在
在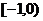 上是增函数,
上是增函数,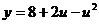 在
在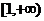 上是减函数,
上是减函数,
所以,函数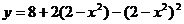 在区间
在区间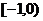 上是减函数
上是减函数
③当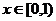 时,
时,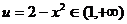 ,
,
而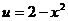 在
在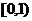 上是减函数,
上是减函数,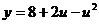 在
在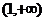 上是减函数,
上是减函数,
所以,函数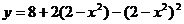 在区间
在区间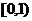 上是增函数
上是增函数
④当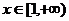 时,
时,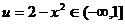 ,
,
而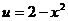 在
在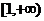 上是增函数,
上是增函数,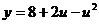 在
在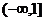 上是减函数,所以,函数
上是减函数,所以,函数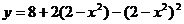 在区间
在区间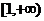 上是减函数
上是减函数
综上所述,函数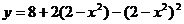 在区间
在区间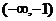 、
、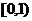 上是增函数;在区间
上是增函数;在区间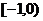 、
、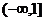 上是减函数
上是减函数
另外,本题给出的复合函数是偶函数,在讨论具有奇偶性的函数的单调性时,应注意应用其奇函数或偶函数的性质,以使解题过程简捷、清楚、具有条理性
1.函数单调性的证明
例1.判断并证明函数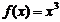 的单调性
的单调性
证明:设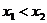 则
则
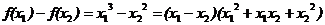
∵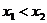 ∴
∴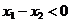 ,
,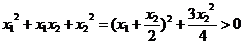 ,
,
∴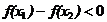 即
即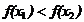 (注:关键
(注:关键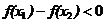 的判断)
的判断)
∴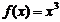 在R上是增函数.
在R上是增函数.
3.判断证明函数单调性的一般步骤是:⑴设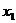 ,
,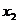 是给定区间内的任意两个值,且
是给定区间内的任意两个值,且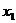 <
<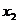 ;⑵作差
;⑵作差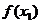 -
-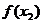 ,并将此差式变形(要注意变形的程度);⑶判断
,并将此差式变形(要注意变形的程度);⑶判断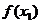 -
-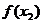 的正负(要注意说理的充分性);⑷根据
的正负(要注意说理的充分性);⑷根据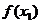 -
-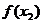 的符号确定其增减性.
的符号确定其增减性.
2.若函数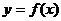 在某个区间是增函数或减函数,则就说函数
在某个区间是增函数或减函数,则就说函数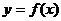 在这一区间具有(严格的)单调性,这一区间叫做函数
在这一区间具有(严格的)单调性,这一区间叫做函数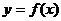 的单调区间.此时也说函数是这一区间上的单调函数.
的单调区间.此时也说函数是这一区间上的单调函数.
1.对于函数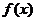 的定义域I内某个区间上的任意两个自变量的值
的定义域I内某个区间上的任意两个自变量的值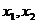
⑴若当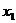 <
<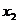 时,都有
时,都有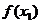 <
<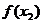 ,则说
,则说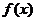 在这个区间上是增函数;
在这个区间上是增函数;
⑵若当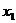 <
<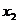 时,都有
时,都有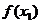 >
>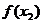 ,则说
,则说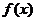 在这个区间上是减函数.
在这个区间上是减函数.
7. 已知全集U={1,2,3,4},A={x|x2-5x+m=0,x∈U},
求CUA、m.
解:将x=1、2、3、4代入x2-5x+m=0中,m=4、6.
当m=4时,A={1,4};
m=6时,A={2,3}.
故满足题条件:CUA={2,3},m=4;CUA={1,4},m=6.
6. 已知A={0,2,4},CUA={-1,1},CUB={-1,0,2},求B=
 利用文恩图,B={1,4}
利用文恩图,B={1,4}
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com