
12、0或-2 13、 14、
14、  和1
和1
6、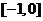 7、
7、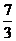 8、
8、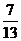 9、
9、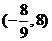 10、
10、 11、
11、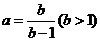
1、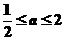 2、
2、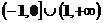 3、
3、 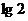 ;4、
;4、 5、
5、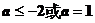
20、(本小题满分16分)
定义在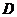 上的函数
上的函数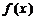 ,如果满足:对任意
,如果满足:对任意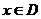 ,存在常数
,存在常数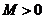 ,都有
,都有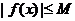 成立,则称
成立,则称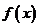 是
是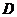 上的有界函数,其中
上的有界函数,其中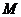 称为函数
称为函数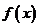 的上界.
的上界.
已知函数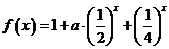 ;
;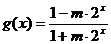 .
.
(1)当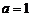 时,求函数
时,求函数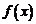 在
在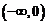 上的值域,并判断函数
上的值域,并判断函数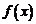 在
在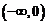 上是否为有界函数,请说明理由;
上是否为有界函数,请说明理由;
(2)若函数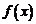 在
在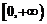 上是以3为上界的有界函数,求实数
上是以3为上界的有界函数,求实数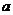 的取值范围;
的取值范围;
(3)若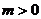 ,函数
,函数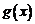 在
在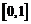 上的上界是
上的上界是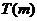 ,求
,求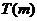 的取值范围.
的取值范围.
2011届常州北郊中学高三学情分析(二)2010.9
19、(本小题满分16分)
已知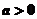 ,函数
,函数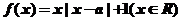 .
.
(1)当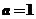 时,求所有使
时,求所有使 成立的
成立的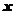 的值;
的值;
(2)当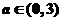 时,求函数
时,求函数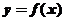 在闭区间
在闭区间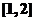 上的最小值;
上的最小值;
(3)试讨论函数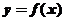 的图像与直线
的图像与直线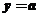 的交点个数.
的交点个数.
18、(本小题满分15分)
设函数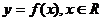 .
.
(1)若函数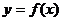 为偶函数并且图像关于直线
为偶函数并且图像关于直线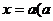
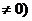 对称,求证:函数
对称,求证:函数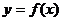 为周期函数.
为周期函数.
(2)若函数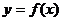 为奇函数并且图像关于直线
为奇函数并且图像关于直线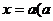
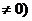 对称,求证:函数
对称,求证:函数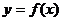 是以
是以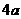 为周期的函数.
为周期的函数.
(3)请对(2)中求证的命题进行推广,写出一个真命题,并予以证明.
17、(本小题满分15分)
国际上常用恩格尔系数(记作n)来衡量一个国家和地区人民生活水平的状况,它的计算公式为: ,各种类型家庭的n如下表所示:
,各种类型家庭的n如下表所示:
|
家庭类型 |
贫困 |
温饱 |
小康 |
富裕 |
最富裕 |
|
n |
n>60% |
50%<n≤60% |
40%<n≤50% |
30%<n≤40% |
n≤30% |
根据某市城区家庭抽样调查统计,2003年初至2007年底期间,每户家庭消费支出总额每年平均增加720元,其中食品消费支出总额每年平均增加120元。
(1)若2002年底该市城区家庭刚达到小康,且该年每户家庭消费支出总额9600元,问2007年底能否达到富裕?请说明理由。
(2)若2007年比2002年的消费支出总额增加36%,其中食品消费支出总额增加12%,问从哪一年底起能达到富裕?请说明理由。
16、(本小题满分14分)
记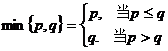 .若函数
.若函数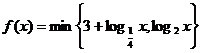 ,
,
(1)用分段函数形式写出函数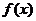 的解析式;(2)求
的解析式;(2)求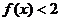 的解集.
的解集.
15、(本小题满分14分)
已知集合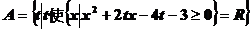 ,
,
集合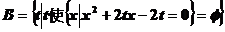 ,其中
,其中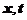 均为实数,
均为实数,
(1)求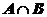 ,(2)设
,(2)设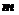 为实数,
为实数,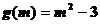 ,求
,求
14、对于函数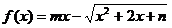 (
(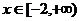 ),若存在闭区间
),若存在闭区间
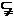
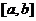
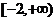
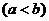 ,使得对任意
,使得对任意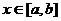 ,恒有
,恒有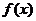 =
=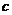 (
(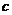 为实常数),则实数
为实常数),则实数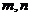 的值依次为 ▲ .
的值依次为 ▲ .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com