
4.欧拉示性数:在欧拉公式中令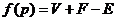 ,
,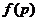 叫欧拉示性数
叫欧拉示性数
 (1)简单多面体的欧拉示性数
(1)简单多面体的欧拉示性数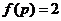 .(2)带一个洞的多面体的欧拉示性数
.(2)带一个洞的多面体的欧拉示性数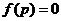

(3)多面体所有面的内角总和公式:①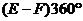 或②
或②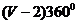
5  球的概念:与定点距离等于或小于定长的点的集合,叫做球体,简称球
球的概念:与定点距离等于或小于定长的点的集合,叫做球体,简称球 定点叫球心,定长叫球的半径
定点叫球心,定长叫球的半径 与定点距离等于定长的点的集合叫做球面
与定点距离等于定长的点的集合叫做球面 一个球或球面用表示它的球心的字母表示,例如球
一个球或球面用表示它的球心的字母表示,例如球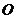 .
.
3.欧拉定理(欧拉公式):简单多面体的顶点数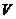 、面数
、面数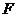 及棱数
及棱数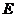 有关系式:
有关系式: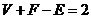 .
.
2. 五种正多面体的顶点数、面数及棱数:
五种正多面体的顶点数、面数及棱数:
|
正多面体 |
顶点数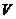 |
面数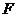 |
棱数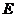 |
|
正四面体 |
4 |
4 |
6 |
|
正六面体 |
8 |
6 |
12 |
|
正八面体 |
6 |
8 |
12 |
|
正十二面体 |
20 |
12 |
30 |
|
正二十面体 |
12 |
20 |
30 |
1.简单多面体:考虑一个多面体,例如正六面体,假定它的面是用橡胶薄膜做成的,如果充以气体,那么它就会连续(不破裂)变形,最后可变为一个球面 如图:象这样,表面经过连续变形可变为球面的多面体,叫做简单多面体
如图:象这样,表面经过连续变形可变为球面的多面体,叫做简单多面体 棱柱、棱锥、正多面体等一切凸多面体都是简单多面体
棱柱、棱锥、正多面体等一切凸多面体都是简单多面体
7. 斜三棱柱的底面的边长是4cm的正三角形,侧棱长为3cm,侧棱
斜三棱柱的底面的边长是4cm的正三角形,侧棱长为3cm,侧棱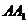 与底面相邻两边都成
与底面相邻两边都成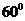 角.(1)求证:侧面
角.(1)求证:侧面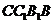 是矩形;
是矩形;
(2)求这个棱柱的侧面积;(3)求棱柱的体积.
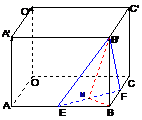
6.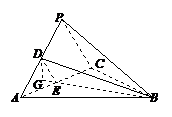 在三棱锥
在三棱锥 中,
中,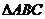 为正三角形,
为正三角形,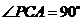 ,
, 为
为 中点,二面角
中点,二面角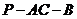 为
为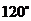 ,
,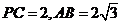 ,(1)求证:
,(1)求证: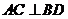 ;(2)求
;(2)求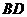 与底面
与底面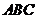 所成的角,(3)求三棱锥
所成的角,(3)求三棱锥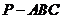 的体积.
的体积.
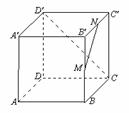
5. 如图,M、N分别是棱长为1的正方体 的棱
的棱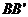 、
、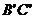 的中点.求异面直线MN与
的中点.求异面直线MN与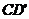 所成的角.
所成的角.
4. 棱长为
棱长为 的正方体
的正方体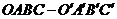 中,
中,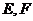 分别为棱
分别为棱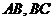 上的动点,且
上的动点,且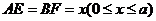 , (1)求证:
, (1)求证: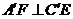 ;
;
(2)当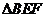 的面积取得最大值时,求二面角
的面积取得最大值时,求二面角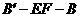 的大小.
的大小.
3.已知:正四棱柱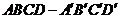 的底面边长为
的底面边长为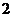 ,侧棱长为
,侧棱长为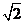 ,
,
(1)求二面角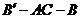 的大小;(2)求点
的大小;(2)求点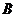 到平面
到平面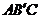 的距离
的距离
17.棱柱的侧面积是指所有侧面面积之和: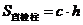 (
(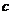 为底面周长,
为底面周长,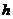 是高,即直棱柱的侧棱长)
是高,即直棱柱的侧棱长)
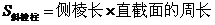
 18.棱柱的体积:
18.棱柱的体积: 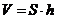

练习:
 1
1 ?判断下列结论是否正确,为什么?(1)有一个面是多边形,其余各面是三角形的几何体是棱锥;
?判断下列结论是否正确,为什么?(1)有一个面是多边形,其余各面是三角形的几何体是棱锥;
(2)正四面体是四棱锥;(3)侧棱与底面所成的角相等的棱锥是正棱锥;
(4)侧棱长相等,各侧面与底面所成的角相等的棱锥是正棱锥.
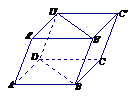
2  如图平行六面体
如图平行六面体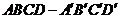 中,
中,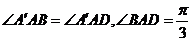 ,
,

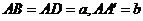 ,求对角面
,求对角面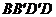 的面积
的面积
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com