
3.等角定理:若一个角的两边和另一个角的两边分别平行并且方向相同,则这两个角相等
1  空间两直线的位置关系(1)相交--有且只有一个公共点;(2)平行--在同一平面内,没有公共点;(3)异面--不在任何一个平面内,没有公共点;
空间两直线的位置关系(1)相交--有且只有一个公共点;(2)平行--在同一平面内,没有公共点;(3)异面--不在任何一个平面内,没有公共点;
2.公理4 :平行于同一条直线的两条直线互相平行 推理模式:
推理模式: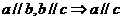 .
.
10. 已知:空间四边形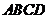 ,
,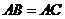 ,
,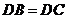 ,求证:
,求证:
证明:取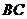 中点
中点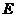 ,连结
,连结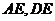 ,∵
,∵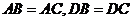 ,∴
,∴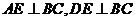 ,
,
∴ 平面
平面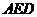 ,又∵
,又∵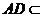 平面
平面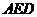 ,∴
,∴ .
.
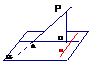
9.如图,已知ABCD是矩形,SA⊥平面ABCD,E是SC上一点.
求证:BE不可能垂直于平面SCD.
证明:用到反证法,假设BE⊥平面SCD,
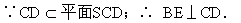 ∵ AB∥CD;∴AB⊥BE.
∵ AB∥CD;∴AB⊥BE.


∴ AB⊥SB,这与Rt△SAB中∠SBA为锐角矛盾.
∴ BE不可能垂直于平面SCD 
8.点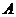 为
为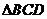 所在平面外的一点,点
所在平面外的一点,点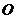 为点
为点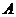 在平面
在平面 内的射影,
内的射影,
若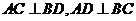 ,求证:
,求证: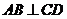 .
.
证明:连结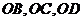 ,∵
,∵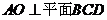 ,且
,且
∴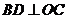 (三垂线定理逆定理)
(三垂线定理逆定理)
同理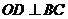 ,∴
,∴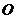 为
为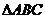 的垂心,∴
的垂心,∴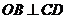 ,
,
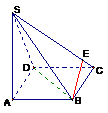 又∵
又∵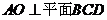 ,∴
,∴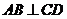 (三垂线定理)
(三垂线定理)
3.能否作一条直线同时垂直于两条相交直线?能否作一条直线同时垂直于两个相交平面?为什么?
答案:(能,而且有无数条) (不能)
4 拿一张矩形的纸对折后略为展开,竖立在桌面上,说明折痕为什么和桌面垂直
拿一张矩形的纸对折后略为展开,竖立在桌面上,说明折痕为什么和桌面垂直
答案:因为折痕垂直于桌面内的两条相交直线.
5 一条直线垂直于一个平面内的两条平行直线,这条直线垂直于这个平面吗?为什么?
一条直线垂直于一个平面内的两条平行直线,这条直线垂直于这个平面吗?为什么?
答案:不一定.因为这条直线可能与这个平面斜交或在其内.
6 过一点和一条直线垂直的平面是否只有一个?为什么?
过一点和一条直线垂直的平面是否只有一个?为什么?
答案:是.假若有两个平面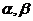 过点A都于
过点A都于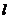 垂直,过这条公共垂线
垂直,过这条公共垂线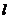 作一个不经过两平面
作一个不经过两平面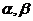 的交线的平面
的交线的平面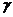 ,
,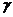 与
与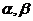 分别相交于直线
分别相交于直线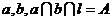 且
且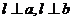 ,
,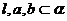 ,从而有
,从而有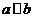 ,此与
,此与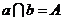 矛盾.
矛盾.
7 如果三条直线共点,且两两垂直,问其中一条直线是否垂直于另两条直线所确定的平面
如果三条直线共点,且两两垂直,问其中一条直线是否垂直于另两条直线所确定的平面
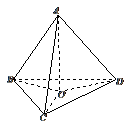 答案:是
答案:是
2.(1)过直线外一点作直线的垂线有 条;垂面有 个;平行线有 条;平行平面有 个.(2)过平面外一点作该平面的垂线有 条;垂面有 个;平行线有 条;平行平面有 个.
答案:(1)无数,一,一,无数;(2)一,无数,无数,一
1.(1)“直线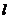 垂直于平面a内的无数条直线”是“
垂直于平面a内的无数条直线”是“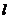 ⊥a”的 ( )
⊥a”的 ( )
(A)充分条件(B)必要条件(C)充要条件(D)既不充分也不必要条件
(2)如果一条直线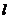 与平面a的一条垂线垂直,那么直线
与平面a的一条垂线垂直,那么直线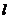 与平面a的位置关系是( )
与平面a的位置关系是( )
(A)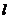 Ìa (B)
Ìa (B)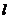 ⊥a (C)
⊥a (C)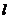 ∥a (D)
∥a (D)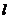 Ìa或
Ìa或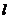 ∥a 答案:(1)B (2)D
∥a 答案:(1)B (2)D
12.三垂线定理的逆定理:在平面内的一条直线,如果和这个平面的一条斜线垂直,那麽它也和这条斜线的射影垂直 推理模式:
推理模式:
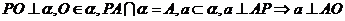 .
.
注意:⑴三垂线指PA,PO,AO都垂直α内的直线a 其实质是:斜线和平面内一条直线垂直的判定和性质定理
其实质是:斜线和平面内一条直线垂直的判定和性质定理 ⑵要考虑a的位置,并注意两定理交替使用
⑵要考虑a的位置,并注意两定理交替使用
基本题型:
10.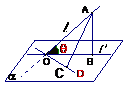 直线和平面所成角(1)定义:平面的一条斜线和它在平面上的射影所成的锐角叫做这条斜线和这个平面所成的角
直线和平面所成角(1)定义:平面的一条斜线和它在平面上的射影所成的锐角叫做这条斜线和这个平面所成的角 一直线垂直于平面,所成的角是直角
一直线垂直于平面,所成的角是直角
一直线平行于平面或在平面内,所成角为0°角。直线和平面所成角范围: [0,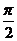 ]
]
 (2)定理:斜线和平面所成角是这条斜线和平面内经过斜足的直线所成的一切角中最小的角
(2)定理:斜线和平面所成角是这条斜线和平面内经过斜足的直线所成的一切角中最小的角
11  三垂线定理 在平面内的一条直线,如果它和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直
三垂线定理 在平面内的一条直线,如果它和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直
说明:(1)定理的实质是判定平面内的一条直线和平面的一条斜线的垂直关系;
(2)推理模式: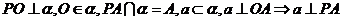

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com