
2. 连续掷两次骰子,以先后得到的点数m、n为点P(m,n)的坐标,那么点P在圆x2+y2=17外部的概率应为( )
(A)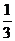 (B)
(B)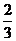 (C)
(C)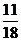 (D)
(D)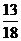

1.
甲、乙两人独立地解同一问题,甲解决这个问题的概率是p1,乙解决这个问题的概率
是p2,那么恰好有1人解决这个问题的概率是 ( )
(A)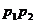 (B)
(B)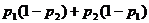 (C)
(C)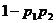 (D)
(D)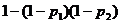

2. 已知两名射击运动员的射击水平,让他们各向目标靶射击10次,其中甲击中目标7次,乙击中目标6次,若在让甲、乙两人各自向目标靶射击3次中,求:(1)甲运动员恰好击中目标2次的概率是多少?(2)两名运 动员都恰好击中目标2次的概率是多少?(结果保留两位有效数字)
解. 甲运动员向目标靶射击1次,击中目标的概率为7/10=0.7
乙运动员向目标靶射击1次,击中目标的概率为6/10=0.6
(1)甲运动员向目标靶射击3次,恰好都击中目标2次的概率是
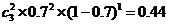

(2)乙运动员各向目标靶射击3次,恰好都击中目标2次的概率是
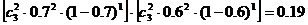

 作业
作业
1. 某班数学兴趣小组有男生和女生各3名,现从中任选2名学生去参加校数学竞赛,求
(I) 恰有一名参赛学生是男生的概率;
(II)至少有一名参赛学生是男生的概率;
(Ⅲ)至多有一名参赛学生是男生的概率.
解:基本事件的种数为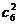 =15种
=15种

(Ⅰ)恰有一名参赛学生是男生的基本事件有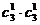 =9种
=9种 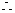 所求事件概率P1=
所求事件概率P1=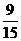 =0.6
=0.6

(Ⅱ)至少有一名参赛学生是男生这一事件是由两类事件构成的,即恰有一名参赛学生是男生和两名参赛学生都是男生,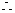 所求事件概率P2=
所求事件概率P2=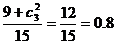

(Ⅲ)至多有一名参赛学生是男生这一事件也是由两类事件构成的,即参赛学生没有男生和恰有一名参赛学生是男生, 所求事件概率P3=
所求事件概率P3=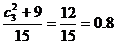

3、从整体入手不是只要结论
知识重要,运用知识解决实际问题的能力更重要。这是现代社会对人才的要求。我们推进素质教育正是为了适应这一要求。素质教育的核心,一是培养提高学生的实践能力,二是培养学生的创新意识。实践能力、创新意识从哪里来?惟一途径是在教学过程中获得。语文教学中要培养提高学生的语文能力和创新意识的问题也只能从教学过程中解决。因此,整体把握课文的训练过程要比整体把握课文得到的结论重要得多。课文是作者观点、态度和感情的载体,我们整体感知课文,了解作者的观点、态度和感情的过程,又是训练提高学生能力和培养学生创新意识的载体。获得结论是重要的,获得结论的过程更重要。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com