
1.解决直线和圆锥曲线的位置关系问题时,一般是消元得到一元二次方程,再讨论二次项的系数和判别式Δ,有时借助图形的几何性质更为方便.
[例1]求过点(0,2)的直线被椭圆x2+2y2=2所截弦的中点的轨迹方程.
解:设直线方程为y=kx+2,
把它代入x2+2y2=2,
整理得(2k2+1)x2+8kx+6=0.
要使直线和椭圆有两个不同交点,则Δ>0,即k<-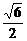 或k>
或k>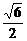 .
.
设直线与椭圆两个交点为A(x1,y1)、B(x2,y2),中点坐标为C(x,y),则
x=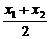 =
=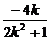 ,
,
y= 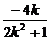 +2=
+2=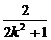 .
.
|
|
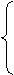 x=
x=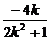 ,
,
y=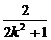
消去k得x2+2(y-1)2=2,
且|x|<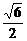 ,0<y<
,0<y<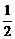 .
.
[例2](2005江西文)
如图,M是抛物线上y2=x上的一点,动弦ME、MF分别交x轴于A、B两点,且MA=MB.
(1)若M为定点,证明:直线EF的斜率为定值;
(2)若M为动点,且∠EMF=90°,求△EMF的重心G的轨迹方程.
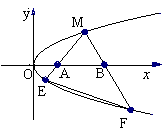

解:(1)设M(y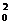 ,y0),直线ME的斜率为k(l>0)
,y0),直线ME的斜率为k(l>0)
则直线MF的斜率为-k,
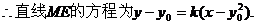
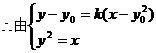 消
消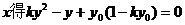
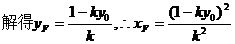
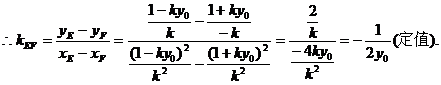
所以直线EF的斜率为定值
(2)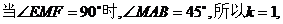
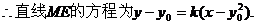
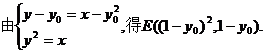
同理可得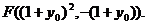
设重心G(x, y),则有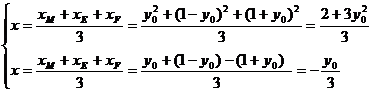
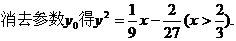
[例3](2006浙江)如图,椭圆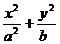 =1(a>b>0)与过点A(2,0)B(0,1)的直线有且只有一个公共点T,且椭圆的离心率e=
=1(a>b>0)与过点A(2,0)B(0,1)的直线有且只有一个公共点T,且椭圆的离心率e=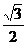 .
(Ⅰ)求椭圆方程;
.
(Ⅰ)求椭圆方程;
(Ⅱ)设F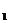 、F
、F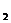 分别为椭圆的左、右焦点,M为线段
分别为椭圆的左、右焦点,M为线段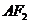 的中点,求证:∠ATM=∠AF
的中点,求证:∠ATM=∠AF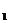 T.
T.


解:(I)过点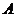 、
、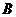 的直线方程为
的直线方程为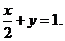
因为由题意得 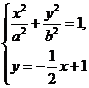 有惟一解,
有惟一解,
即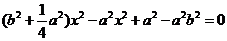 有惟一解,
有惟一解,
所以
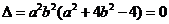 (
(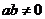 ),
),
故 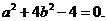
又因为
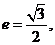 即
即 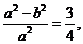
所以 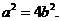
从而得 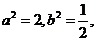
故所求的椭圆方程为 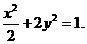
(II)由(I)得 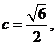 故
故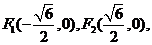
从而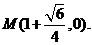
由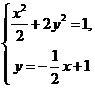
解得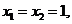 所以
所以 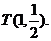
因为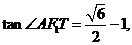
又
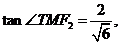 得
得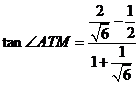
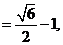
因此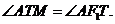
[例4]已知椭圆C: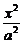 +
+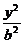 =1(a>b>0),两个焦点分别为F1和F2,斜率为k的直线l过右焦点F2且与椭圆交于A、B两点,设l与y轴交点为P,线段PF2的中点恰为B.
=1(a>b>0),两个焦点分别为F1和F2,斜率为k的直线l过右焦点F2且与椭圆交于A、B两点,设l与y轴交点为P,线段PF2的中点恰为B.
(1)若|k|≤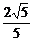 ,求椭圆C的离心率的取值范围;
,求椭圆C的离心率的取值范围;
(2)若k=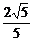 ,A、B到右准线距离之和为
,A、B到右准线距离之和为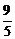 ,求椭圆C的方程.
,求椭圆C的方程.
解:(1)设右焦点F2(c,0),则l:y=k(x-c).
令x=0,则y=-ck,∴P(0,-ck).
∵B为F2P的中点,∴B(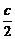 ,-
,- ).
).
∵B在椭圆上,∴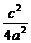 +
+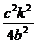 =1.
=1.
∴k2=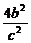 ·
·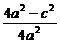 =(
=(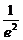 -1)(4-e2)
-1)(4-e2)
=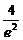 +e2-5.
+e2-5.
∵|k|≤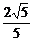 ,∴
,∴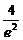 +e2-5≤
+e2-5≤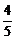 .
.
∴(5e2-4)(e2-5)≤0.
∴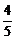 ≤e2<1.∴
≤e2<1.∴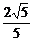 ≤e<1.
≤e<1.
(2)k=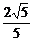 ,∴e=
,∴e=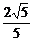 .∴
.∴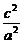 =
=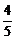 .
.
∴a2=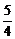 c2,b2=
c2,b2=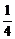 c2.椭圆方程为
c2.椭圆方程为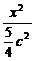 +
+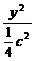 =1,即x2+5y2=
=1,即x2+5y2=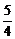 c2.
c2.
直线l方程为y=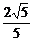 (x-c),
(x-c),
B(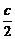 ,-
,-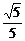 c),右准线为x=
c),右准线为x=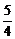 c.
c.
设A(x0,y0),则
(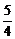 c-x0)+(
c-x0)+(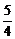 c-
c-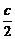 )=
)=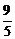 ,
,
∴x0=2c-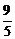 ,y0=
,y0=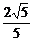 (c-
(c-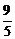 ).
).
∵A在椭圆上,
∴(2c-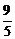 )2+5[
)2+5[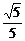 (c-
(c-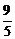 )]2=
)]2=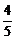 c2.
c2.
解之得c=2或c=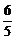 (不合题意,舍去).
(不合题意,舍去).
∴椭圆方程为x2+5y2=5,即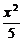 +y2=1.
+y2=1.
[研讨.欣赏](2006山东)双曲线C与椭圆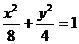 有相同的焦点,直线
有相同的焦点,直线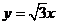 为C的一条渐近线。
为C的一条渐近线。
(1)求双曲线C的方程;
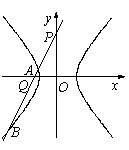
(2)过点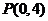 的直线
的直线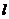 ,交双曲线C于A、B两点,交
,交双曲线C于A、B两点,交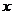 轴于Q点(Q点与C的顶点不重合),当
轴于Q点(Q点与C的顶点不重合),当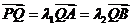 ,且
,且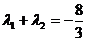 时,求
时,求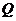 点的坐标。
点的坐标。
解:(Ⅰ)设双曲线方程为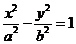
由椭圆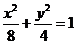 求得两焦点为
求得两焦点为 ,
,
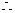 对于双曲线
对于双曲线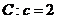 ,又
,又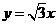 为双曲线
为双曲线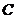 的一条渐近线
的一条渐近线
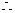
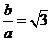 解得
解得 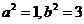 ,
,
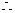 双曲线
双曲线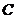 的方程为
的方程为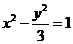

(Ⅱ)解法一:
由题意知直线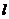 的斜率
的斜率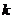 存在且不等于零。
存在且不等于零。
设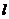 的方程:
的方程: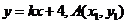 ,
,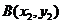
则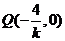
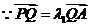
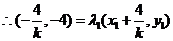
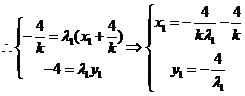
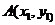 在双曲线
在双曲线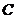 上,
上,
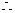
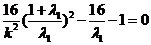
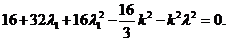
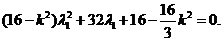
同理有: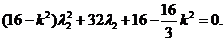
若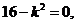 则直线
则直线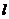 过顶点,不合题意.
过顶点,不合题意.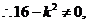
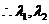 是二次方程
是二次方程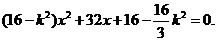 的两根.
的两根.
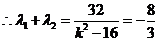
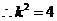 ,
,
此时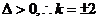 .
.
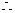 所求
所求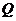 的坐标为
的坐标为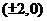 .
.
解法二:
由题意知直线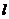 的斜率
的斜率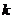 存在且不等于零
存在且不等于零
设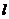 的方程,
的方程,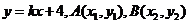 ,则
,则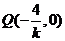 .
.
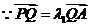 ,
,
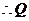 分
分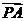 的比为
的比为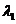 .
.
由定比分点坐标公式得
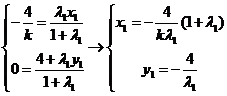
下同解法一
解法三:
由题意知直线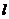 的斜率
的斜率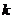 存在且不等于零
存在且不等于零
设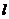 的方程:
的方程: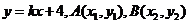 ,则
,则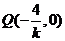 .
.
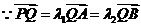 ,
,
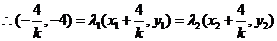 .
.
 ,
,
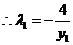 ,
,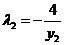 ,
,
又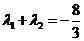 ,
,
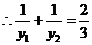
即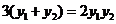
将 代入
代入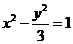 得
得
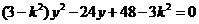
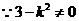 ,否则
,否则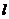 与渐近线平行。
与渐近线平行。
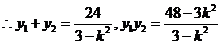 。
。
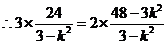
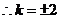
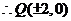
解法四:
由题意知直线l得斜率k存在且不等于零,设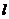 的方程:
的方程: ,
,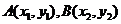
则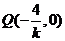
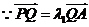 ,
,
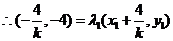 。
。
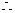
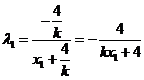
同理 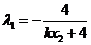
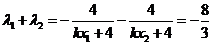 .
.
即 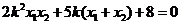 。 (*)
。 (*)
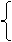 又
又 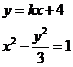
消去y得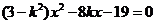 .
.
当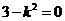 时,则直线l与双曲线得渐近线平行,不合题意,
时,则直线l与双曲线得渐近线平行,不合题意,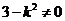 。
。
由韦达定理有:
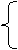
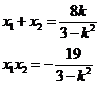
代入(*)式得 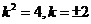
 所求Q点的坐标为
所求Q点的坐标为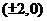 。
。
6.设P(x0,y0)则d1·d2=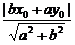 ·
·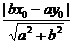 =
=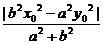 =
=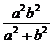
6.双曲线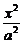 -
-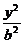 =1(a>0,b>0)上任意一点到它的两条渐近线的距离之积等于________.
=1(a>0,b>0)上任意一点到它的两条渐近线的距离之积等于________.
.
简答:1-3。CAC; 4. 32; 5. 作出函数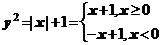 的图象,如图所示:
的图象,如图所示:
所以,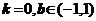 ;
;
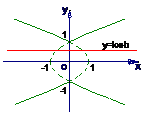
5.(2006上海) 若曲线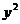 =|
=|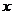 |+1与直线
|+1与直线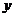 =
=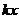 +
+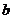 没有公共点,则
没有公共点,则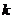 、
、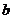 分别应满足的条件是
分别应满足的条件是
4.(2006山东)已知抛物线 ,过点
,过点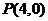 的直线与抛物线相交于
的直线与抛物线相交于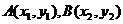 两点,则
两点,则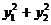 的最小值是
。
的最小值是
。
3.(2006福建)已知双曲线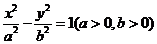 的右焦点为F,若过点F且倾斜角为
的右焦点为F,若过点F且倾斜角为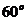 的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是( )
的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是( )
(A)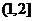 (B)
(B)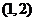 (C)
(C)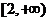 (D)
(D)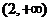
2.(2006全国Ⅰ)抛物线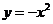 上的点到直线
上的点到直线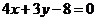 距离的最小值是 ( )
距离的最小值是 ( )
A 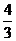 B
B
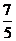 C
C 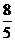 D
D 
1.(2004全国I)设抛物线y2=8x的准线与x轴交于点Q,若过点Q的直线l与抛物线有公共点,则直线l 的斜率的取值范围是 ( )
A.[-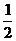 ,
,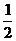 ] B.[-2,2] C.[-1,1] D.[-4,4]
] B.[-2,2] C.[-1,1] D.[-4,4]
5.弦长公式:
圆锥曲线与直线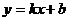 交于A(x1,y1),B(x2,y2),则弦长
交于A(x1,y1),B(x2,y2),则弦长
 ;
;
与直线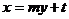 A(x1,y1),B(x2,y2),则弦长
A(x1,y1),B(x2,y2),则弦长
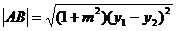

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com