
1.P(a,b)点在双曲线上,则有a2-b2=1,即(a+b)(a-b)=1.
d=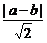 =
=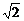 , ∴|a-b|=2.
, ∴|a-b|=2.
又P点在右支上,则有a>b, ∴a-b=2.
∴|a+b|×2=1,a+b=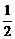 .
.
6.过抛物线y2=4x焦点的直线交抛物线于A、B两点,已知|AB|=8,O为坐标原点,则△OAB的重心的横坐标为________.
简答提示:1-4.BCDD;
5.已知(4,2)是直线l被椭圆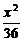 +
+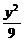 =1所截得的线段的中点,则l的方程是____________.
=1所截得的线段的中点,则l的方程是____________.
4.直线y=x+3与曲线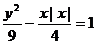 ( )
( )
A.没有交点 B.只有一个交点 C.有两个交点 D.有三个交点
[填空题]
3.(2006辽宁)直线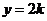 与曲线
与曲线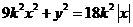
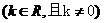 的公共点的个数为( )
的公共点的个数为( )
(A)1 (B)2 (C)3 (D)4
2.已知对k∈R,直线y-kx-1=0与椭圆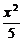 +
+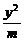 =1恒有公共点,则实数m的取值范围是
=1恒有公共点,则实数m的取值范围是
A.(0,1) B.(0,5)
C.[1,5)∪(5,+∞) D.[1,5)
1.若双曲线x2-y2=1的右支上一点P(a,b)到直线y=x的距离为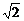 ,则a+b的值为 (
)
,则a+b的值为 (
)
A.-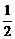 B.
B.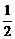 C.±
C.±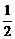 D.±2
D.±2
4.涉及到圆锥曲线焦点弦、焦半径问题,可以利用焦半径公式或圆锥曲线的第二定义,应掌握求焦半径以及利用焦半径解题的方法.
同步练习 8.4直线和圆锥曲线的位置关系
[选择题]
3.求圆锥曲线的弦长时,可利用弦长公式
d=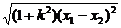 =
=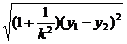 .
.
再结合韦达定理,设而不求整体解决.焦点弦的长也可以直接利用焦半径公式处理,可以使运算简化.
2.涉及弦的中点问题,除利用韦达定理外,也可以运用“点差法”,但必须以直线与圆锥曲线相交为前提,否则不宜用此法.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com