
1.
含有三个实数的集合可表示为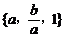 ,也可表示为
,也可表示为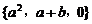 ,则
,则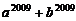 的值为
A.0 B.-1 C.1 D.±1
的值为
A.0 B.-1 C.1 D.±1
22.(本小题满分14分)
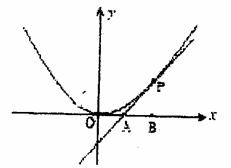
如图,已知直线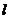 与抛物线
与抛物线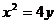 相切于点P(2,1),且与
相切于点P(2,1),且与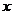 轴交于点A,定点B的坐标为(2,0)。
轴交于点A,定点B的坐标为(2,0)。
(I)若动点M满足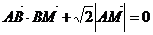 ,求点M的轨迹C;
,求点M的轨迹C;
(II)若过点B的直线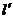 (斜率不等于零)与(I)中的轨迹C交于不同的两点E、F(E在B、F之间),试求
(斜率不等于零)与(I)中的轨迹C交于不同的两点E、F(E在B、F之间),试求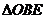 与
与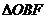 面积之比的取值范围。
面积之比的取值范围。
21.(本小题满分12分)
若函数f(x)=ax3+bx2+cx+d是奇函数,且f(x)极小值=f(-)=-.
(1)求函数f(x)的解析式;
(2)求函数f(x)在[-1,m](m>-1)上的最大值;
(3)设函数g(x)=,若不等式g(x)·g(2k-x)≥(-k)2在(0,2k)上恒成立,求实数k的取值范围.
20.(本小题满分12分)
设方程tan2πx-4tanπx+=0在[n-1,n)(n∈N*)内的所有解之和为an.
(1)求a1、a2的值,并求数列{an}的通项公式;
(2)设数列{bn}满足条件:b1=2,bn+1≥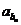 ,求证:
,求证:
++…+<2.
19.(本小题满分12分)
在一个盒子中,放有标号分别为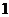 ,
,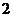 ,
,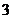 的三张卡片,现从这个盒子中,有放回地先后抽得两张卡片的标号分别为
的三张卡片,现从这个盒子中,有放回地先后抽得两张卡片的标号分别为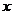 、
、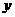 ,记
,记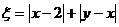 .(Ⅰ)求随机变量
.(Ⅰ)求随机变量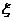 的最大值,并求事件“
的最大值,并求事件“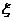 取得最大值”的概率;(Ⅱ)求随机变量
取得最大值”的概率;(Ⅱ)求随机变量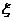 的分布列和数学期望.
的分布列和数学期望.
18.(本小题满分12分)
已知函数f(x)=asinωx-acosωx(a>0,ω>0)的图象上两相邻最高点的坐标分别为 学
学
(,2)和(,2).
(1) 求a与ω的值;
(2) 在△ABC中,a、b、c分别是角A、B、C的对边,
(1)
且f(A)=2, 求的值.
求的值.
17.(本小题满分12分)
设命题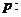 函数
函数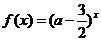 是
是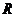 上的减函数,命题
上的减函数,命题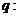 函数
函数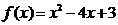
在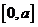 的值域为
的值域为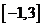 .若“
.若“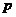 且
且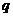 ”为假命题,“
”为假命题,“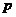 或
或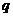 ”为真命题,求
”为真命题,求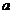 的取值范围.
的取值范围.
16.给出定义:若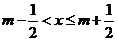 (其中
(其中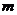 为整数),则
为整数),则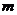 叫做离实数
叫做离实数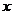 最近的整数,记作
最近的整数,记作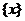 ,即
,即 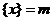 . 在此基础上给出下列关于函数
. 在此基础上给出下列关于函数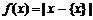 的四个命题:
①函数
的四个命题:
①函数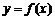 的定义域是R,值域是[0,
的定义域是R,值域是[0,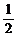 ];
];
②函数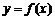 的图像关于直线
的图像关于直线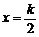 (k∈Z)对称;
(k∈Z)对称;
③函数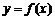 是周期函数,最小正周期是1;
是周期函数,最小正周期是1;
④ 函数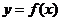 在
在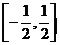 上是增函数;
上是增函数;
则其中真命题是__ .
15.已知 F1 、F2是椭圆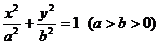 的两个焦点,椭圆上存在一点P,使得S
⊿F1PF2=
的两个焦点,椭圆上存在一点P,使得S
⊿F1PF2=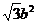 ,则该椭圆的离心率的取值范围是
。
,则该椭圆的离心率的取值范围是
。
14.已知平面上的向量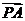 、
、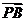 满足
满足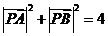 ,
,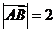 ,设向量
,设向量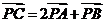 ,则
,则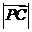 的最小值是
.
的最小值是
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com