
17.(本题满分12分)
已知正四棱柱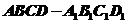 底面边长是1,体积是2,
底面边长是1,体积是2,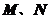 分别是棱
分别是棱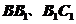 的中点,求异面直线
的中点,求异面直线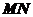 与
与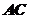 所成角的大小.(结果用反三角函数值表示)
所成角的大小.(结果用反三角函数值表示)

16.已知图1中的图像对应的函数为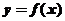 ,则图2中的图像对应的函数在下列给出的四式中,只可能是
( )
,则图2中的图像对应的函数在下列给出的四式中,只可能是
( )
A.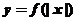 B.
B.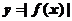 C.
C.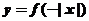 D.
D.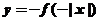

15.已知数列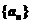 的前
的前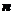 项和
项和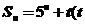 是实数),下列结论正确的是
( )
是实数),下列结论正确的是
( )
A.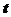 为任意实数,
为任意实数,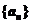 均是等比数列 B.当且仅当
均是等比数列 B.当且仅当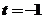 时,
时,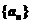 是等比数列
是等比数列
C.当且仅当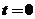 时,
时,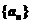 是等比数列 D.当且仅当
是等比数列 D.当且仅当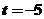 时,
时,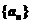 是等比数列
是等比数列
14.已知直线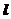 与抛物线
与抛物线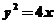 相交于
相交于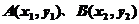 两个不同的点,那么“直线
两个不同的点,那么“直线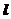 经过抛物线
经过抛物线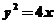 的焦点”是“
的焦点”是“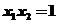 ”的
( )
”的
( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分又不必要条件
13.复数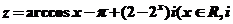 是虚数单位),在复平面内的对应点只可能位于( )
是虚数单位),在复平面内的对应点只可能位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
12.如图,在平面斜坐标系中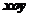 中,
中,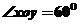 ,平面上任一点
,平面上任一点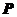 的斜坐标定义如下:若
的斜坐标定义如下:若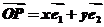 ,其中
,其中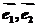 分别为与
分别为与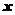 轴,
轴,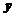 轴同方向的单位向量,则点
轴同方向的单位向量,则点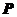 的斜坐标为
的斜坐标为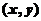 .
.
那么,以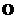 为圆心,
为圆心,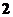 为半径的圆有斜坐标系
为半径的圆有斜坐标系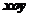 中的方程是__________.
中的方程是__________.
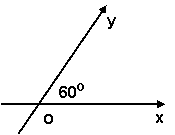
11.如果执行下面的程序框图,那么输出的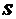 =_________ .
=_________ .

10.若一个球的体积为 ,则它的表面积为___________.
,则它的表面积为___________.
9.在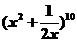 的二项展开式中,
的二项展开式中, 的系数是___________.
的系数是___________.
8.若方程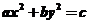 的系数
的系数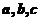 可以从
可以从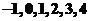 这
这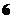 个数中任取
个数中任取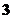 个不同的数而得到,则这样的方程表示焦点在
个不同的数而得到,则这样的方程表示焦点在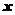 轴上的椭圆的概率是___________.(结果用数值表示)
轴上的椭圆的概率是___________.(结果用数值表示)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com