
2. 复数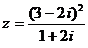 在复平面上对应的点位于 ( )
在复平面上对应的点位于 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
1、定义集合M与N的新运算:M+N=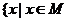 或
或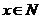 且
且 ,则(M+N)+N等于( )
,则(M+N)+N等于( )
A、M B、N
C、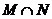 D、
D、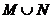
(13) 不等式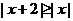 的解是
.
的解是
.
(14) 由动点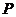 向圆
向圆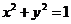 引两条切线
引两条切线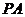 、
、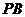 ,切点分别为A、B,
,切点分别为A、B, ,则动点
,则动点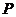 的轨迹方程为_________________________.
的轨迹方程为_________________________.
(15)过点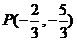 作直线与双曲线
作直线与双曲线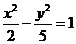 交于
交于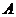 、
、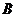 两点,若线段
两点,若线段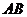 的中点恰为
的中点恰为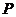 点,则
点,则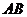 所在的直线方程是_______________________.
所在的直线方程是_______________________.
(16)若数列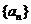 满足
满足 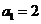 ,
,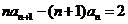 ,则数列
,则数列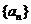 的通项公式
的通项公式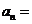 ______________________.
______________________.
豫南七校2008-2009学年度上期期末联考
16.已知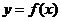 是以2为周期的偶函数,当
是以2为周期的偶函数,当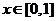 时,
时, 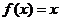 ,那么在区间
,那么在区间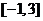 内,关于
内,关于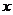 的方程
的方程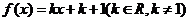 有4个根,则
有4个根,则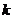 的取值范围为
.
的取值范围为
.
豫南七校2008-2009学年度上期期末联考
15.已知函数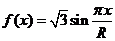 的图象上,相邻的一个最大值点与一个最小值点恰好都在圆
的图象上,相邻的一个最大值点与一个最小值点恰好都在圆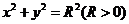 上,则
上,则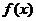 的最小正周期为
.
的最小正周期为
.
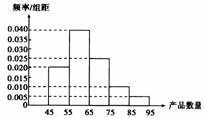
14.为了调查某厂工人生产某种产品的能力,随机抽查了20位工人某天生产该产品的数量,其频率分布直方图如图,则这20名工人中一天生产该产品的数量在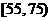 的人数是
.
的人数是
.
13. 已知
已知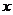 、
、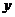 满足
满足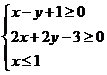 ,则
,则 的最大值是
.
的最大值是
.
22.解:(I)解法一: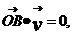 .
. 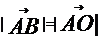 ,既O点和B点关于直线l对称。
,既O点和B点关于直线l对称。
直线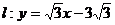 , ① ----------------------------------1分
, ① ----------------------------------1分
过原点垂直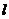 的直线方程为
的直线方程为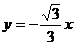 , ②
, ②
解①②得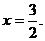 -----------------------------------------------------3分
-----------------------------------------------------3分
∵椭圆中心(0,0)关于直线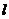 的对称点在椭圆C的右准线上,
的对称点在椭圆C的右准线上,
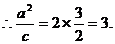
∵直线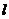 过椭圆焦点,∴该焦点坐标为(2,0).
过椭圆焦点,∴该焦点坐标为(2,0).
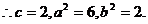 故椭圆C的方程为
故椭圆C的方程为 ③-------6分
③-------6分
解法二:直线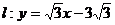 .
.
设原点关于直线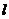 对称点为(p,q),则
对称点为(p,q),则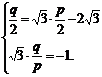 解得p=3.
解得p=3.
∵椭圆中心(0,0)关于直线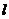 的对称点在椭圆C的右准线上,
的对称点在椭圆C的右准线上,
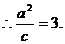
∵直线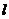 过椭圆焦点,∴该焦点坐标为(2,0).
过椭圆焦点,∴该焦点坐标为(2,0).
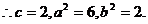 故椭圆C的方程为
故椭圆C的方程为 ③
③
(2)解:若直线MN平行于y轴,则y1+y2=0,不合题意。---------7分
若直线MN不平行于y轴,设过M、N两点的直线方程为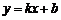 由
由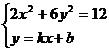 得
得 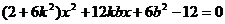 ---------10分
---------10分
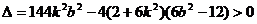 ,即
,即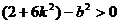 ①
设M (x1,y1),N (x2,y2),则
①
设M (x1,y1),N (x2,y2),则
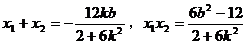 ,∴
,∴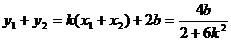 由已知
由已知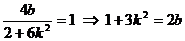 ,代入①得:
,代入①得: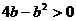 ,即0<b<4
,即0<b<4
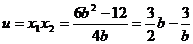 ------------12分
∵
------------12分
∵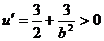 ∴u在(0,4)上是增函数
∴
∴u在(0,4)上是增函数
∴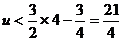 ,故不存在使u≤m成立---------- 14分
,故不存在使u≤m成立---------- 14分
21.解:(1)因为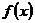 =
=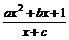 (a>0)为奇函数,所以
(a>0)为奇函数,所以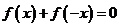 在其定义域内恒成立,
在其定义域内恒成立,
即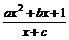 +
+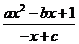 =0恒成立,化简即
=0恒成立,化简即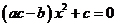 恒成立,
恒成立,
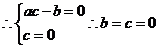 ,
,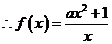
又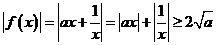 且
且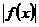 min=
min=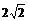 ,
,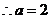

(2)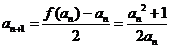 ,
,
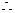
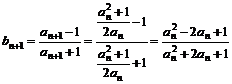 =
=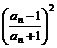 =
=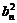
∴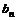 =
=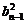 =
=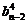 =…=
=…=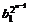 ,而b1=
,而b1=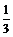 ∴
∴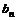 =
=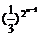
当n=1时, b1=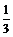 ,命题成立,
,命题成立,
当n≥2时,2n-1=(1+1)n-1=1+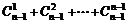 ≥1+
≥1+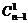 =n
=n
∴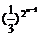 <
<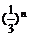 ,即 bn≤
,即 bn≤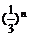 .
.
20.解:(1)PB//平面EAC。 2分
(2)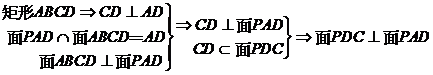
正三角形PAD中,E为PD的中点,所以,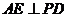 ,
,
又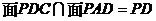 ,所以,AE⊥平面PCD。 6分
,所以,AE⊥平面PCD。 6分
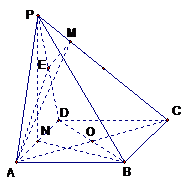 (3)在PC上取点M使得
(3)在PC上取点M使得 。
。
由于正三角形PAD及矩形ABCD,且AD=AB,所以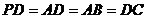
所以,在等腰直角三角形DPC中,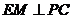 ,
,
连接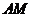 ,因为AE⊥平面PCD,所以,
,因为AE⊥平面PCD,所以,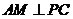 。
。
所以,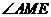 为二面角A-PC-D的平面角。
为二面角A-PC-D的平面角。
在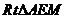 中,
中, 。
。
即二面角A-PC-D的正切值为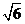 。 10分
。 10分
(4)设N为AD中点,连接PN,则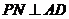 。
。
又面PAD⊥底面ABCD,所以,PN⊥底面ABCD。
所以,NB为PB在面ABCD上的射影。
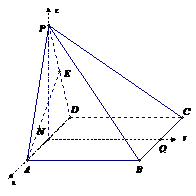 要使PB⊥AC,需且只需NB⊥AC
要使PB⊥AC,需且只需NB⊥AC
在矩形ABCD中,设AD=1,AB=x
则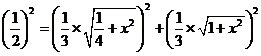 ,
,
解之得: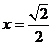 。
。
所以,当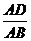
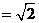 时,PB⊥AC。 14分
时,PB⊥AC。 14分
证法二:(按解法一相应步骤给分)
设N为AD中点,Q为BC中点,则因为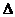 PAD是正三角形,底面ABCD是矩形,所以,
PAD是正三角形,底面ABCD是矩形,所以,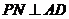 ,
,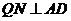 ,又因为侧面PAD⊥底面ABCD,所以,
,又因为侧面PAD⊥底面ABCD,所以,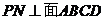 ,
,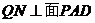 ,
,
以N为坐标原点,NA、NQ、NP所在直线分别为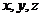 轴如图建立空间直角坐标系。设
轴如图建立空间直角坐标系。设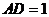 ,
,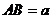 ,则
,则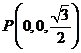 ,
,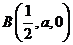 ,
,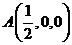 ,
,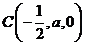 ,
,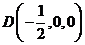 ,
,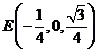 。
。
(2)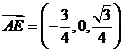 ,
,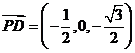 ,
,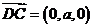 ,
,
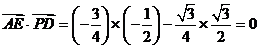 ,
,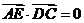
所以,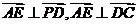 。
。
又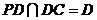 ,
,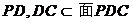 ,所以,AE⊥平面PCD。 6分
,所以,AE⊥平面PCD。 6分
(3)当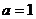 时,由(2)可知:
时,由(2)可知: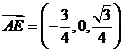 是平面PDC的法向量;
是平面PDC的法向量;
设平面PAC的法向量为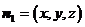 ,则
,则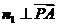 ,
,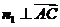 ,即
,即
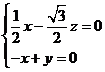 ,取
,取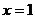 ,可得:
,可得: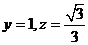 。所以,
。所以,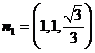 。
。
向量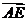 与
与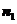 所成角
所成角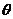 的余弦值为:
的余弦值为: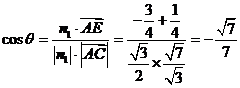 。
。
所以,tan q = 。
又由图可知,二面角A-PC-D的平面角为锐角,所以,二面角A-PC-D的平面角就是向量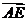 与
与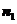 所成角
所成角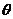 的补角。
的补角。
其正切值等于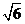 。 10分
。 10分
(4)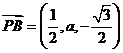 ,
,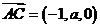 ,令
,令 ,得
,得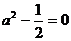 ,所以,
,所以,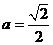 。所以,当
。所以,当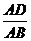
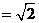 时,PB⊥AC。
时,PB⊥AC。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com