
2、顶点在同一球面上的正四棱柱ABCD-A1B1C1D1中,AB=1,AA1=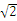 ,则A、C两点间的球面距离为( B )
,则A、C两点间的球面距离为( B )
A .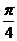 B.
B. 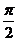 C .
C .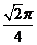 D.
D. 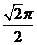
1、设集合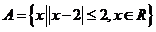 ,
,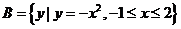 ,则
,则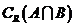 等于( B )
等于( B )
A.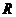 B.
B.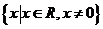 C.
C.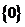 D.
D.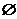
21.(本小题满分14分)
数列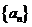 满足:
满足: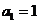 ,
,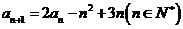 。
。
(1)是否存在常数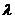 、
、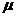 ,使得数列
,使得数列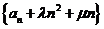 是等比数列.若存在,求出
是等比数列.若存在,求出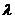 、
、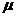 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(2)设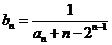 ,
,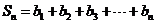 ,证明:当
,证明:当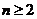 时,
时,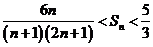 .
.
20.(本小题满分13分)
已知F1、F2是椭圆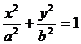 的两个焦点,O为坐标原点,点P
的两个焦点,O为坐标原点,点P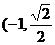 )在椭圆上,
)在椭圆上,
线段PF2与y轴的交点M满足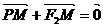 ;⊙O是以F1F2为直径的圆,一直线l: y=kx+m与⊙O相切,并与椭圆交于不同的两点A、B.
;⊙O是以F1F2为直径的圆,一直线l: y=kx+m与⊙O相切,并与椭圆交于不同的两点A、B.
(I)求椭圆的标准方程;
(II)当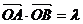 ,且满足
,且满足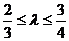 时,求△AOB面积S的取值范围.
时,求△AOB面积S的取值范围.
19.(本小题满分12分)
设x=l是函数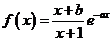 的一个极值点(
的一个极值点(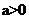 ,
,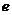 为自然对数的底).
为自然对数的底).
(1)求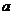 与
与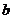 的关系式(用
的关系式(用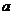 表示
表示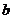 ),并求
),并求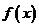 的单调区间;
的单调区间;
(2)若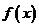 在闭区间
在闭区间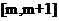 上的最小值为0,最大值为
上的最小值为0,最大值为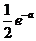 , 且
, 且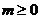 。,试求
。,试求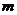 与
与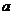 的值.
的值.
18.(本小题满分12分)
下图是某厂节能耗技术改造后生产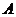 产品过程中记录的产量
产品过程中记录的产量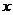 (吨),与相应的生产能耗
(吨),与相应的生产能耗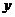 (吨标准煤)的散点图.
(吨标准煤)的散点图.

(1)求出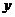 关于
关于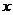 的回归直线方程
的回归直线方程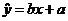 ;
;
(2)现已计算得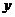 与
与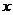 的相关系数
的相关系数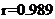 ,试说明(Ⅰ)中所求得的回归直线方程是否具有意义.线性回归方程系数公式
,试说明(Ⅰ)中所求得的回归直线方程是否具有意义.线性回归方程系数公式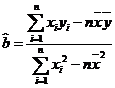 ,
,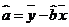
16.(本小题满分12分)已知函数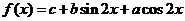 的图象经过点
的图象经过点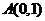 ,
,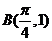 ,且当
,且当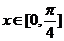 时,
时,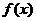 的最大值是2
的最大值是2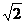 -1.
-1.
(1)求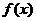 的解析式;
的解析式;
(2)求出满足条件的一个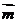 ,使得将
,使得将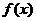 的图象按向量
的图象按向量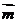 平移后可以得到一个奇函数的图象.
平移后可以得到一个奇函数的图象.
17(本小题满分12分)
如图,已知三棱柱ABC-A1B1C1的侧棱与底面所成的角为60°,AB=BC,A1A=A1C=2,AB⊥BC,侧面AA1C1C⊥底面ABC。
(1) 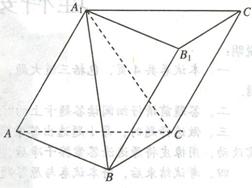 证明:A1B⊥A1C1;
证明:A1B⊥A1C1;
(2) 求二面角A-CC1-B的大小;
(3) 求经过A1、A、B、C四点的球的表面积。
15.已知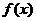 是定义在R上的不恒为零的函数,且对任意
是定义在R上的不恒为零的函数,且对任意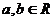 满足下列关系式:
满足下列关系式: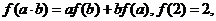
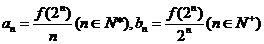 。考察下列结论:①
。考察下列结论:①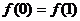 ; ②
; ②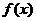 为偶函数;③数列
为偶函数;③数列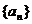 为等比数列;④数列
为等比数列;④数列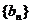 为等差数列,其中正确的结论是
____.
为等差数列,其中正确的结论是
____.
14.已知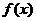 是可导的偶函数,且
是可导的偶函数,且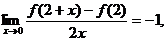 则曲线
则曲线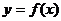 在(-2,1)处的切线方程是
。
在(-2,1)处的切线方程是
。
13.设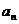 为
为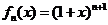 的展开式中含
的展开式中含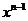 项的系数,则数列
项的系数,则数列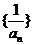 的前n项和为_____
的前n项和为_____
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com