
21. (本小题满分12分)
已知椭圆C: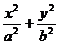 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为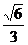 ,短轴一个端点到右焦点的距离为
,短轴一个端点到右焦点的距离为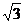 .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设直线l与椭圆C交于A、B两点,坐标原点O到直线l的距离为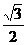 ,求△AOB面积的最大值.
,求△AOB面积的最大值.
20.
解:(1)∵ 点 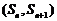 在直线
在直线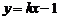 上, ∴
上, ∴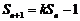 , ……(1分)
, ……(1分)
当n=1时,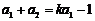 , ……(2分)
, ……(2分)
又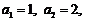 则
则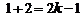 ,∴
,∴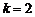
 ……(4分)
……(4分)
(2) 由 (1) 知 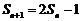 ①, 当
①, 当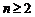 时,
时,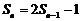 ② ……(6分)
② ……(6分)
①-②,得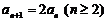 , ……(8分)
, ……(8分)
又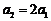 ,易见
,易见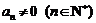 ,∴
,∴ 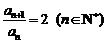 ……(9分)
……(9分)
所以,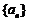 是等比数列. ……(10分)
是等比数列. ……(10分)
(3)由(2)知,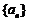 的公比为2, ……(11分)
的公比为2, ……(11分)
所以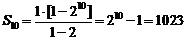 . ……(12分)
. ……(12分)
20.(本题满分12分)
已知数列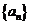 的前
的前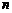 项和为
项和为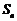 ,
,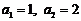 ,且点
,且点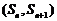 在直线
在直线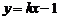 上
上
(1)求k的值;
(2)求证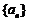 是等比数列;
是等比数列;
(3)求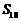 的值.
的值.
19.(本小题满分12分)
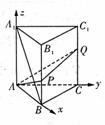
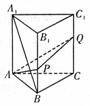 在直三棱柱ABC-A1B1C1中,A1A=AB=3
在直三棱柱ABC-A1B1C1中,A1A=AB=3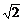 ,AC=3,∠CAB=90°,P、Q分别为棱BB1、CC1上的点,且BP=
,AC=3,∠CAB=90°,P、Q分别为棱BB1、CC1上的点,且BP=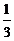 BB1,CQ=
BB1,CQ=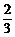 CC1.
CC1.
(1)求平面APQ与面ABC所成的锐二面角的大小.
(2)在线段A1B(不包括两端点)上是否存在一点M,使AM+MC1最小?若存在,求出最小值;若不存在,说明理由.
[解析](1)建立如图所示空间直角坐标系A-xyz.
 A(0,0,0),P(3
A(0,0,0),P(3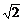 ,0,
,0,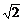 ),Q(0,3,2
),Q(0,3,2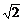 ),
),
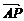 =(3
=(3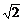 ,0,
,0,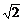 ),
),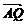 =(0,3,2
=(0,3,2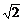 ).
).
设平面APQ的一个法向量为n1=(x,y,z)
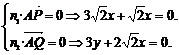
令z=3,则x=-1,y=-2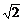 ,∴n1=(-1,-2
,∴n1=(-1,-2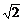 ,3)
,3)
平面ABC的一个法向量n2=(0,0,1).
∴cos〈n1,n2〉=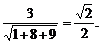
∴平面APQ与面ABC所成的锐角大小为45°. (6分)
(1)问也可用传统方法求解.(并参照计分)
(2)沿A1B将面A1BC1与面A1BA展开,连结AC1与A1B交于点M,此时AM+MC1有最小值.
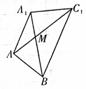 ∵∠A1AB=90°,AA1=AB,∴∠A1AB=45°,又C1A1⊥面ABB1A1,∴C1A1⊥A1B.
∵∠A1AB=90°,AA1=AB,∴∠A1AB=45°,又C1A1⊥面ABB1A1,∴C1A1⊥A1B.
∴△AA1C1中,∠AA1C1=135°
AC1=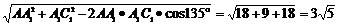 ,
,
∴存在点M,使AM+MC1取最小值为3 . (12分)
. (12分)
17、(本小题满分10分)
设函数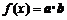 ,其中向量
,其中向量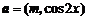 ,
,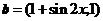 ,
, ,且
,且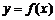 的图象经过点
的图象经过点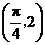 .
.
(Ⅰ)求实数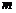 的值;
的值;
(Ⅱ)求函数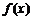 的最小值及此时
的最小值及此时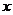 值的集合.
值的集合.
解:(Ⅰ)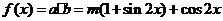 ,
,
由已知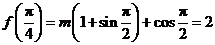 ,得
,得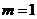 .
.
(Ⅱ)由(Ⅰ)得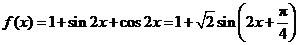 ,
,
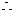 当
当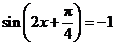 时,
时,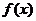 的最小值为
的最小值为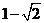 ,
,
由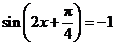 ,得
,得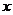 值的集合为
值的集合为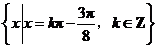 .
.
(18)(本小题满分12分)厂家在产品出厂前,需对产品做检验,厂家将一批产品发给商家时,商家按合同规定也需随机抽取一定数量的产品做检验,以决定是否接收这批产品.
(Ⅰ)若厂家库房中的每件产品合格的概率为0.8,从中任意取出4件进行检验.求至少有1件是合格品的概率;
(Ⅱ)若厂家发给商家20件产品,其中有3件不合格,按合同规定该商家从中任取2件,都进行检验,只有2件都合格时才接收这批产品,否则拒收.求该商家可能检验出不合格产品数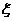 的分布列及期望
的分布列及期望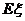 ,并求该商家拒收这批产品的概率.
,并求该商家拒收这批产品的概率.
(18)本题考察相互独立事件、互斥事件等的概率计算,考察随机事件的分布列,数学期望等,考察运用所学知识与方法解决实际问题的能力。
解:(Ⅰ)记“厂家任取4件产品检验,其中至少有1件是合格品”为事件A
用对立事件A来算,有
(Ⅱ)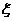 可能的取值为
可能的取值为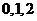
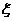
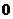
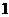
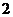
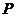
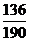
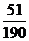
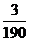
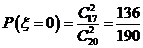 ,
,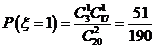 ,
,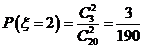
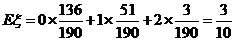
记“商家任取2件产品检验,都合格”为事件B,则商家拒收这批产品的概率
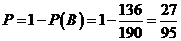
所以商家拒收这批产品的概率为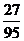
15,
 16,
16,

16、函数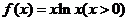 的单调递增区间是____.
的单调递增区间是____.
|
一. |
题目 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
|
答案 |
|
|
|
|
|
|
|
|
|
|
|
|
15.设直线ax-y+3=0与圆(x-1)2+(y-2)2=4相交于A、B两点,且弦长为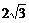 ,则a= 0 .
,则a= 0 .
14、设等差数列 的公差
的公差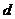 是2,前
是2,前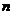 项的和为
项的和为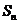 ,则
,则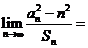 3
3
13.点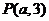 到直线
到直线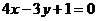 的距离等于4,且在不等式
的距离等于4,且在不等式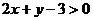 表示的平面区域内,则点P的坐标是 (7,3) .
表示的平面区域内,则点P的坐标是 (7,3) .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com