
5.(2005上海)某班有50名学生,其中15人选修A课程,另外35人选修B课程.从班级中任选两名学生,他们是选修不同课程的学生的概率是__________.(结果用分数表示)
4.(2005重庆)某轻轨列车有4节车厢,现有6位乘客准备乘坐,设每一位乘客进入每节车厢是等可能的,则这6位乘客进入各节车厢的人数恰好为0,1,2,3的概率为 .
3.甲、乙二人参加法律知识竞赛,共有12个不同的题目,其中选择题8个,判断题4个.甲、乙二人各依次抽一题,则甲抽到判断题,乙抽到选择题的概率是 ( )
A. B.
B.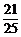 C.
C. D.
D.
[填空题]
3.(2004重庆)某校高三年级举行的一次演讲比赛共有10位同学参加,其中一班有3位,二班有2位,其他班有5位.若采取抽签的方式确定他们的演讲顺序,则一班的3位同学恰好被排在一起(指演讲序号相连),而二班的2位同学不排在一起的概率为 ( )
A.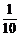 B.
B.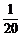 C.
C.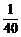 D.
D.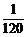
2.从1,2,…,9这九个数中,随机抽取3个不同的数,则这3个数的和为偶数的概率是 ( )
A.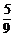 B.
B.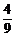 C.
C.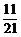 D.
D.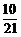
1. (2006福建6)在一个口袋中装有5个白球和3个黑球,这些球除颜色外完全相同。从中摸出3个球,至少摸到2个黑球的概率等于 ( )
A.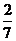 B.
B.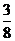 C.
C.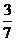 D.
D.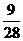
3. 准确理解题意,合理设计解题方案,灵活简洁地运算,谨防重复遗漏.
同步练习 10.5随机事件的概率
[选择题]
2. 熟练掌握等可能性事件概率的求法;
1. 正确理解概率的概念,
[例1]一个口袋里共有2个红球和8个黄球,从中随机地接连取3个球,每次取一个.设{恰有一个红球}=A,{第三个球是红球}=B.求在下列条件下事件A、B的概率.
(1)不返回抽样;(2)返回抽样.
解:(1)不返回抽样,
P(A)= =
=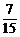 , (与顺序有关),或
, (与顺序有关),或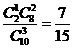 (与顺序无关)
(与顺序无关)
P(B)=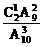 =
= 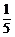 .
.
(2)返回抽样,
P(A)=C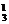
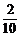 (
(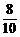 )2=
)2=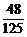 , P(B)=
, P(B)=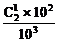 =
= 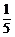 .
.
[例2] 某油漆公司发出10桶油漆,其中白漆5桶,黑漆3桶,红漆2桶.在搬运中所有标签脱落,交货人随意将这些标签重新贴上,问一个定货3桶白漆、2桶黑漆和1桶红漆的顾客,按所定的颜色如数得到定货的概率是多少?
解:随意贴上的标签等于没贴标签,从10桶油漆中随意取.
P(A)=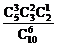 =
=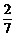 .
.
答:顾客按所定的颜色得到定货的概率是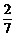 .
.
[例3]将甲、乙两颗骰子先后各抛一次,a、b分别表示抛掷甲、乙两颗骰子所出现的点数.
(1)若a+b<4的事件记为A,求事件A的概率;
(2)若点P(a,b)落在直线x+y=m(m为常数)上,且使此事件的概率最大,求m的值.
解:(1)基本事件总数为6×6=36.
|
和 |
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
6 |
7 |
8 |
9 |
10 |
11 |
12 |
当a=1时,b=1,2,3;
当a=2时,b=1,2;
当a=3时,b=1.
共有(1,1),(1,2),(1,3),(2,1),(2,2),
(3,1)6个点适合题设,
∴P(A)= =
=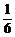 .
.
(2)由表可知,m=7所含的基本事件最多,
发生的概率最大此时P= =
= 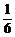 最大.
最大.
[例4] (2004全国Ⅱ)已知8支球队中有3支弱队,以抽签方式将这8支球队分为A、B两组,每组4支.求:
(1)A、B两组中有一组恰有两支弱队的概率;
(2)A组中至少有两支弱队的概率.
解:(1)A组中恰有两支弱队,或一只弱队,概率为
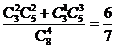 ,(也可按对立事件求: 1
,(也可按对立事件求: 1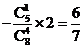 )
)
(2)解法一:A组中至少有两支弱队的概率为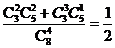
(也可分为互斥的的两部分算: 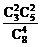 +
+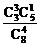 =
=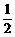 )
)
解法二:A、B两组有一组至少有两支弱队的概率为1,由于对A组和B组来说,至少有两支弱队的概率是相同的,所以A组中至少有两支弱队的概率为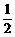 .
.
[研讨.欣赏]
(1)从0、2、4、6、8这五个数字中任取2个,从1、3、5、7、9这五个数字中任取1个。能组成多少个没有重复数字的三位数?在这些三位数中任取一个恰好能被5整除的概率是多少?
(2)从1、2、3……10这10个数字中有放回的抽取3次,每次抽取一个数字,求三次抽取中最小数是3的概率。
解:(1)若取0则有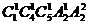 =80个三位数,若不取0,则有
=80个三位数,若不取0,则有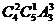 =180,所以共有80+180=260个三位数;而被5整除的三位数为:若0为个位数的有
=180,所以共有80+180=260个三位数;而被5整除的三位数为:若0为个位数的有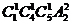 =40个,若5为个位数,则含0有
=40个,若5为个位数,则含0有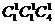 =4个,不含0有
=4个,不含0有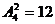 个,所以是5的倍数共有40+4+12=56个。故所求的概率P=
个,所以是5的倍数共有40+4+12=56个。故所求的概率P= 。
。
答:在这些三位数中任取一个恰好能被5整除的概率是。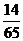
(2)有放回都抽取3次共有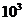 个结果,因最小的数是3可分为:恰有一个3的有
个结果,因最小的数是3可分为:恰有一个3的有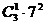 个,恰有2个3的有
个,恰有2个3的有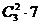 个,恰有3个3的有
个,恰有3个3的有 个,所以所求概P=
个,所以所求概P=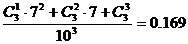 。
。
答:三次抽取中最小数有3的概率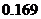 .
.
◆提炼方法:等可能性事件的概率,只需求出分母和分子,关键是确定“分子”条件,正确运用排列组合、计数原理算出分子的数目。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com