
19.已知b>-1,c>0,函数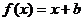 的图象与函数
的图象与函数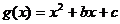 的图象相切.
的图象相切.
(1)设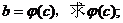
(2)是否存在常数c,使得函数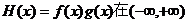 内有极值点?若存在,求出c的取值范围;若不存在,请说明理由.
内有极值点?若存在,求出c的取值范围;若不存在,请说明理由.
18.
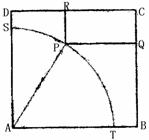 如图,四边形ABCD是一个边长为100米的正方形地皮,其中ATPS是一半径为90米的扇形小山,其余部分都是平地,P是弧TS上一点,现有一位开发商想在平地上建造一个两边落在BC与CD上的长方形停车场PQCR.
如图,四边形ABCD是一个边长为100米的正方形地皮,其中ATPS是一半径为90米的扇形小山,其余部分都是平地,P是弧TS上一点,现有一位开发商想在平地上建造一个两边落在BC与CD上的长方形停车场PQCR.
(1)若∠PAT=θ,试写出四边形RPQC的面积S关于θ
的函数表达式,并写出定义域;
(2)试求停车场的面积最大值.
17.已知函数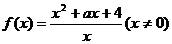 .
.
(1)若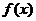 为奇函数,求a的值;(2)若
为奇函数,求a的值;(2)若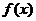 在
在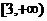 上恒大于0,求a的取值范围.
上恒大于0,求a的取值范围.
16.已知函数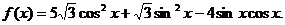
(1)当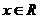 时,求
时,求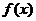 的最小值;(2)若
的最小值;(2)若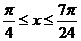 ,求
,求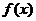 的单调区间.
的单调区间.
15.在数列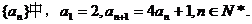
(1)证明数列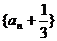 是等比数列;(2)求数列{
是等比数列;(2)求数列{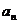 }的前n项和Sn.
}的前n项和Sn.
14.规定一种运算: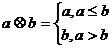 ,例如:1
,例如:1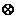 2=1,3
2=1,3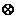 2=2,则函数
2=2,则函数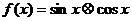 的值域为
..
的值域为
..
12.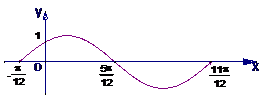 函数
函数
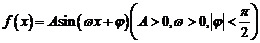 的一段图象过点
的一段图象过点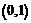 ,如图所示,函数
,如图所示,函数 的解析式___
.
的解析式___
.
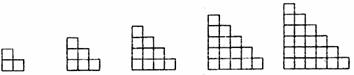 13.观察下列的图形中小正方形的个数,则第6个图中有
个小正方形.
13.观察下列的图形中小正方形的个数,则第6个图中有
个小正方形.
11.曲线 在
在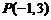 处的切线方程为
.
处的切线方程为
.
9.已知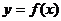 是定义在R上的奇函数,且
是定义在R上的奇函数,且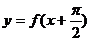 为偶函数,对于函数
为偶函数,对于函数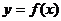 有下列几种描述
有下列几种描述
①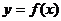 是周期函数 ②
是周期函数 ②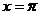 是它的一条对称轴
是它的一条对称轴
③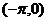 是它图象的一个对称中心 ④当
是它图象的一个对称中心 ④当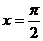 时,它一定取最大值
时,它一定取最大值
其中描述正确的是 .
|
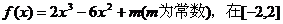 上有最大值3,那么此函数在[-2,2]上的最小值为
.
上有最大值3,那么此函数在[-2,2]上的最小值为
.8.已知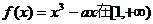 上是单调增函数,则a的最大值是
.
上是单调增函数,则a的最大值是
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com