2、小船渡河问题分析

[例9]一条宽度为L的河，水流速度为v_s，已知船在静水中的航速为v_c，那么，(1)怎样渡河时间最短？(2)若v_s＜v_c怎样渡河位移最小？(3)若v_s＞v_c，怎样渡河船漂下的距离最短？

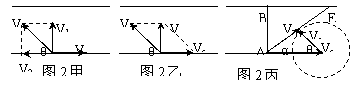分析与解：(1)如图2甲所示，设船上头斜向上游与河岸成任意角θ，这时船速在垂直于河岸方向的速度分量V₁=V_csinθ,渡河所需时间为：.

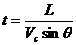可以看出：L、V_c一定时，t随sinθ增大而减小；当θ=90⁰时，sinθ=1,所以，当船头与河岸垂直时，渡河时间最短，.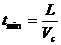

(2)如图2乙所示，渡河的最小位移即河的宽度。为了使渡河位移等于L，必须使船的合速度V的方向与河岸垂直。这是船头应指向河的上游，并与河岸成一定的角度θ。根据三角函数关系有：V_ccosθ─V_s=0.

所以θ=arccosV_s/V_c,因为0≤cosθ≤1,所以只有在V_c>V_s时，船才有可能垂直于河岸横渡。

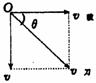
(3)如果水流速度大于船上在静水中的航行速度，则不论船的航向如何，总是被水冲向下游。怎样才能使漂下的距离最短呢？如图2丙所示，设船头V_c与河岸成θ角，合速度V与河岸成α角。可以看出：α角越大，船漂下的距离x越短，那么，在什么条件下α角最大呢？以V_s的矢尖为圆心，以V_c为半径画圆，当V与圆相切时，α角最大，根据cosθ=V_c/V_s,船头与河岸的夹角应为：θ=arccosV_c/V_s.

船漂的最短距离为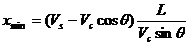：.　 此时渡河的最短位移为：.

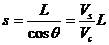思考：①小船渡河过程中参与了哪两种运动？这两种运动有何关系？

②过河的最短时间和最短位移分别决定于什么？

3.重点掌握的两种情况：一是加速度大小、方向都不变的曲线运动，叫匀变曲线运动，如平抛运动；另一是加速度大小不变、方向时刻改变的曲线运动，如匀速圆周运动．

规律方法　 1、运动的合成与分解的应用

合运动与分运动的关系：满足等时性与独立性．即各个分运动是独立进行的，不受其他运动的影响，合运动和各个分运动经历的时间相等，讨论某一运动过程的时间，往往可直接分析某一分运动得出．

[例2]小船从甲地顺水到乙地用时t₁，返回时逆水行舟用时t₂，若水不流动完成往返用时t₃，设船速率与水流速率均不变，则(　　　 )

　 A．t₃＞t₁+t₂ ；　 B．t₃＝t₁+t₂；　 C．t₃＜t₁+t₂ ；　 D．条件不足，无法判断

解析：设船的速度为V，水的速度为v₀，则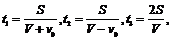

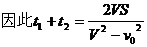
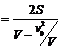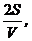<故选C

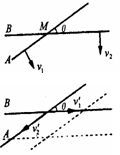[例3]如图所示，A、B两直杆交角为θ，交点为M，若两杆各以垂直于自身的速度V₁、V₂沿着纸面运动，则交点M的速度为多大？

　 解析：如图所示，若B杆不动，A杆以V₁速度运动，交点将沿B杆移动，速度为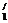V，V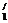=V₁／sinθ．若A杆不动，B杆移动时，交点M将沿A杆移动，速度为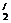V，V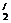=V₂／sinθ．两杆一起移动时，交点M的速度v_M可看成两个分速度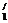V和V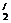的合速度，故v_M的大小为v_M==

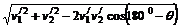[例4]玻璃板生产线上，宽9m的成型玻璃板以4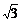m／s的速度连续不断地向前行进，在切割工序处，金刚钻的走刀速度为8m／s，为了使割下的玻璃板都成规定尺寸的矩形，金刚钻割刀的轨道应如何控制？切割一次的时间多长？

　解析：要切成矩形则割刀相对玻璃板的速度垂直v，如图设v_刀与v_玻方向夹角为θ，cosθ=v_玻/v_刀=4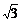/8，则θ=30⁰。v=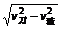==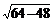4m/s。时间t=s/v=9/4=2·45s

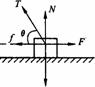
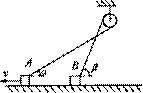
[例5]如图所示的装置中，物体A、B的质量m_A＞m_B。最初，滑轮两侧的轻绳都处于竖直方向，若用水平力F向右拉A，起动后，使B匀速上升。设水平地面对A的摩擦力为f,绳对A的拉力为T，则力f,T及A所受合力F_合的大小()

A.F_合≠O,f减小，T增大；B.F_合≠O,f增大，T不变；

C. F_合＝O,f增大，T减小；D. F_合＝O,f减小，T增大；

分析:显然此题不能整体分析。B物体匀速上升为平衡状态，所受的绳拉力T恒等于自身的重力，保持不变。A物体水平运动，其速度可分解为沿绳长方向的速度(大小时刻等于B物体的速度)和垂直于绳长的速度(与B物体的速度无关)，写出A物体速度与B物体速度的关系式，可以判断是否匀速，从而判断合力是否为零。

解：隔离B物体：T=m_Bg，保持不变。隔离A物体：受力分析如图所示，设绳与水平线夹角为θ，则：

①随A物体右移，θ变小，由竖直平衡可以判断支持力变大。由f=μN，得f变大。

②将A物体水平运动分解如图所示，有v_B＝v_Acosθ，故随θ变小，cosθ变大，V_B不变，V_A变小，A物体速度时时改变，必有F_合≠O。

所得结论为：F_合≠O，f变大，T不变。B项正确。

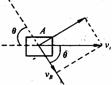
[例6]两个宽度相同但长度不同的台球框固定在水平面上，从两个框的长边同时以相同的速度分别发出小球A和B，如图所示，设球与框边碰撞时无机械能损失，不计摩擦，则两球回到最初出发的框边的先后是(　　 )

A. A球先回到出发框边　　　 B球先回到出发框边

C.两球同时回到出发框边　　　 D.因两框长度不明，故无法确定哪一个球先回到出发框边

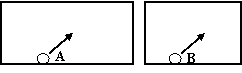解析：小球与框边碰撞无机械能损失，小球每次碰撞前后的运动速率不变，且遵守反射定律。以A球进行分析，如图。

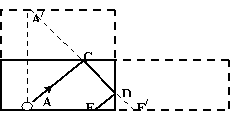小球沿AC方向运动至C处与长边碰后，沿CD方向运动到D处与短边相碰，最后沿DE回到出发边。经对称得到的直线A^/CDE^/的长度与折线ACDE的总长度相等。

框的长边不同，只要出发点的速度与方向相同，不论D点在何处，球所通过的总路程总是相同的，不计碰撞时间，故两球应同时到达最初出发的框边。答案：C

也可用分运动的观点求解：小球垂直于框边的分速度相同，反弹后其大小也不变，回到出发边运动的路程为台球桌宽度的两倍，故应同时回到出发边。

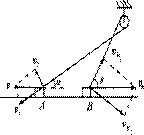
[例7]如图所示，A、B两物体系在跨过光滑定滑轮的一根轻绳的两端，当A物体以速度v向左运动时，系A,B的绳分别与水平方向成a、β角，此时B物体的速度大小为　　　　　　 ，方向水平向右

解析：根据A,B两物体的运动情况，将两物体此时的速度v和v_B分别分解为两个分速度v₁(沿绳的分量)和v₂(垂直绳的分量)以及v_B1(沿绳的分量)和v_B2(垂直绳的分量)，如图，由于两物体沿绳的速度分量相等，v₁＝v_B1，vcosα＝v_Bcosβ.

则B物体的速度方向水平向右，其大小为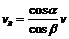

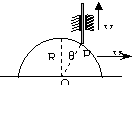[例8]一个半径为R的半圆柱体沿水平方向向右以速度V₀匀速运动。在半圆柱体上搁置一根竖直杆，此杆只能沿竖直方向运动，如图7所示。当杆与半圆柱体接触点P与柱心的连线与竖直方向的夹角为θ，求竖直杆运动的速度。

解析：设竖直杆运动的速度为V₁，方向竖直向上，由于弹力方向沿OP方向，所以V₀、V₁在OP方向的投影相等，即有　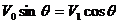 ，解得V₁=V₀.tgθ.

2．物体做一般曲线运动的条件：运动物体所受的合外力(或加速度)的方向跟它的速度方向不在同一直线上(即合外力或加速度与速度的方向成一个不等于零或π的夹角)．

说明：当物体受到的合外力的方向与速度方向的夹角为锐角时，物体做曲线运动速率将增大，当物体受到的合外力的方向与速度方向的夹角为钝角时，物体做曲线运动的速率将减小。

1．曲线运动是指物体运动的轨迹为曲线；曲线运动的速度方向是该点的切线方向；曲线运动速度方向不断变化，故曲线运动一定是变速运动．

(1)等时性：合运动所需时间和对应的每个分运动所需时间相等．

(2)独立性：一个物体可以同时参与几个不同的分运动，各个分运动独立进行，互不影响．

(3)等效性:合运动和分运动是等效替代关系，不能并存；

(4)矢量性:加速度、速度、位移都是矢量，其合成和分解遵循平行四边形定则。

[例1]如图所示的塔吊臂上有一可以沿水平方向运动的小车A，小车下装有吊着物体B的吊钩．在小车A与物体B以相同的水平速度沿吊臂方向匀速运动的同时，吊钩将物体B向上吊起，A、B之间的距离以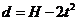 (SI)(SI表示国际单位制，式中H为吊臂离地面的高度)规律变化，则物体做

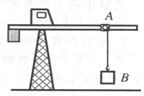(A)速度大小不变的曲线运动．　 (B)速度大小增加的曲线运动．

(C)加速度大小方向均不变的曲线运动．

(D)加速度大小方向均变化的曲线运动． 答案：B C

4．速度分解的一个基本原则就是按实际效果来进行分解，常用的思想方法有两种：一种思想方法是先虚拟合运动的一个位移，看看这个位移产生了什么效果，从中找到运动分解的办法；另一种思想方法是先确定合运动的速度方向(物体的实际运动方向就是合速度的方向)，然后分析由这个合速度所产生的实际效果，以确定两个分速度的方向．

3．将速度正交分解为 v_x＝vcosα和v_y=vsinα是常用的处理方法．

2．运动分解也遵循矢量运算的平行四边形定则．

1．已知合运动求分运动叫运动的分解．

下面的作文有哪些方面值得我们学习的呢？

等待成功

众里寻他千百度，蓦然回首，那人却在灯火阑珊处。　

种子播进土里，我们要等着它破土而出；严冬冻僵了我们的思绪，我们要等着春风的到来；母亲孕育了一个新的生命，我们要等着他慢慢成熟……很多事物都需要在等待中不断地酝酿，一味不切实际的主动，只能是好高鹜远，结果可能是适得其反。　

美丽需要等待。野草走过寒冬，只为等待被春风再一次唤醒；青松历经风霜，为的是等待明年的春暖花开；蛹化蝴蝶，需要在等待中完成从最丑陋的毛毛虫到美丽的蝴蝶的蜕变；蝉四年黑暗中的苦工，只为等待一个月阳光下的欢唱……等待中孕育着美丽，等待中酝酿着重生。　

生命需要等待。从最初的胚芽长到枝繁叶茂；从最初的幼苗长成参天大树，从满树的花香到满树的果实……寒来暑往需要等待。熊猫憨态可掬的样子很可爱，但要等待着它慢慢长大；孩子成才固然可喜，但要等待他十年寒窗后的金榜题名……春华秋实也需要等待。　

成功需要等待。鸿门宴上刘邦的隐忍是为了等待着自己羽翼丰满一举击溃敌人的时刻；越王勾践的十年生聚十年教训，卧薪尝胆是为了等待报仇雪耻的机会；诸葛孔明躬耕陇亩是为了等待一个匡扶社稷的明主以实现自己的远大抱负……很多时候成功就是一种等待的过程。

当然，等待不是消极，而是一种蓄势待发；等待不是逃避，而是一种积极的面对。任何事物都有从量变到质变的积累。拔苗助长，只能换来禾苗枯死的结局，不等着成熟就忙着收割的庄稼，最后收获的也只会是一把秕谷；生命不等着孕育成熟就忙着出生，也只会使生命过早地凋落。　

是啊，生命中有着许许多多的等待。等待不是无所事事，等待不是空想其成，等待不是碌碌无为，等待不是不思进取，等待不能患得患失，等待不能好高鹜远，等待不能放弃，等待不能失意。等待要坚定不移，等待要沉着冷静，等待要一份信念，等待要一份真诚。但自耕耘，莫问收获，努力争取，成功就会在那蓦然回首的灯火阑珊处。

点评：本文在素材的使用上，选用保罗·高尔文、霍金等国外的例子，侯德榜等国内事例，很好地阐释了文章的主题：放开双手，让梦想自由飞翔。