
8.(2008·
江西理,13)直角坐标平面内三点A(1,2)、B(3,-2)、C(9,7),若E、F为线段BC的三等分点,则 ·
·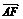 =
.
=
.
答案 22
7.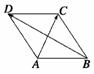 (2008·天津理,14)如图所示,在平行四边形ABCD中,
(2008·天津理,14)如图所示,在平行四边形ABCD中,
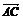 =(1,2),
=(1,2),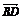 =(-3,2),则
=(-3,2),则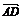 ·
·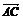 =
.
=
.
答案 3
6.(2009·成化高级中学高三期中)已知3a+4b+5c=0,且|a|=|b|=|c|=1,则a·(b+c)= .
答案 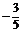
5.已知a,b是非零向量,且满足(a-2b)⊥a,(b-2a)⊥b,则a与b的夹角是 .
答案 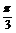
4.若a与b-c都是非零向量,则“a·b=a·c”是“a⊥(b-c)”的 条件.
答案 充要
3.已知向量a,b满足|a|=1,|b|=4,且a·b=2,则a与b的夹角为 .
答案 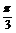
2.若向量a,b满足|a|=1,|b|=2,a与b的夹角为60°,则a·b+b·b的值为 .
答案 5
1.点O是三角形ABC所在平面内的一点,满足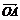 ·
·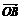 =
=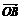 ·
· 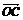 =
=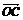 ·
·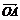 ,则点O是△ABC的 心.
,则点O是△ABC的 心.
答案 垂
12.已知在直三棱柱ABC-A1B1C1中,AC⊥BC,D为AB的中点,AC=BC=BB1.求证:
(1)BC1⊥AB1;
(2)BC1∥平面CA1D.
证明 如图所示,以C1为原点,C1A1,C1B1,C1C所在直线分别为x轴、y轴、z轴建立空间直角坐标系.不妨设AC=2,由于AC=BC=BB1,则A(2,0,2),B(0,2,2),C(0,0,2),A1(2,0,0),B1(0,2,0),C1(0,0,0),D(1,1,2).
(1)由于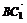 =(0,-2,-2),
=(0,-2,-2),
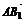 =(-2,2,-2),
=(-2,2,-2),
所以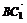 ·
·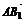 =0-4+4=0,因此
=0-4+4=0,因此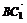 ⊥
⊥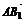 ,
,
故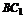 ⊥
⊥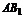 .
.
(2)方法一 取A1C的中点E,连接DE,由于E(1,0,1),
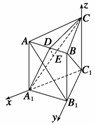 所以
所以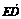 =(0,1,1),又
=(0,1,1),又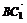 =(0,-2,-2),
=(0,-2,-2),
所以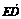 =-
=- ·
·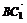 ,又因为ED和BC1不共线,
,又因为ED和BC1不共线,
所以ED∥BC1,且DE 平面CA1D,BC1
平面CA1D,BC1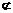 平面CA1D,
平面CA1D,
故BC1∥平面CA1D.
方法二 由于 =(2,0,-2),
=(2,0,-2),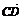 =(1,1,0),
=(1,1,0),
若设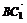 =x
=x +y
+y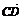 ,
,
则得 ,解得
,解得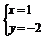 ,
,
即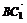 =
= -2
-2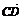 ,
,
所以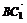 ,
, ,
,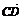 是共面向量,
是共面向量,
又因为BC1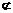 平面CA1D,因此BC1∥平面CA1D.
平面CA1D,因此BC1∥平面CA1D.
方法三 求出平面CA1D的法向量n,证明向量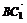 ⊥n.
⊥n.
设n=(a,b,1),由于 =(2,0,-2),
=(2,0,-2),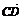 =(1,1,0)
=(1,1,0)
∴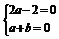 ,∴
,∴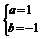
∴n=(1,-1,1),又∵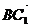 =(0,-2,-2),
=(0,-2,-2),
∴n·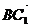 =2-2=0,∴
=2-2=0,∴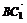 ⊥n,
⊥n,
又∵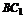
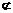 平面CA1D,∴
平面CA1D,∴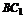 ∥平面CA1D.
∥平面CA1D.
11.在正方体ABCD-A1B1C1D1中,E、F分别是BB1、CD的中点.
(1)求证:平面AED⊥平面A1FD1;
(2)在AE上求一点M,使得A1M⊥平面ADE.
(1)证明 建立如图所示的空间直角坐标系D-xyz,
不妨设正方体的棱长为2,
则A(2,0,0),E(2,2,1),
F(0,1,0),A1(2,0,2),D1(0,0,2),
设平面AED的法向量为n1=(x1,y1,z1),
则n1·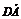 =(x1,y1,z1)·(2,0,0)=0,
=(x1,y1,z1)·(2,0,0)=0,
n1·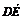 =(x1,y1,z1)·(2,2,1)=0,
=(x1,y1,z1)·(2,2,1)=0,
∴2x1=0,2x1+2y1+z1=0.
令y1=1,得n1=(0,1,-2),
同理可得平面A1FD1的法向量n2=(0,2,1).
∵n1·n2=0,∴n1⊥n2,
∴平面AED⊥平面A1FD1.
(2)解 由于点M在直线AE上,
设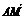 =
=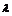
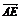 =
=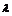 (0,2,1)=(0,2
(0,2,1)=(0,2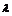 ,
,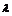 ).
).
可得M(2,2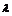 ,
,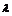 ),∴
),∴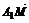 =(0,2
=(0,2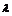 ,
,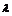 -2),
-2),
∵AD⊥A1M,∴要使A1M⊥平面ADE,
只需A1M⊥AE,
∴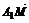 ·
·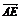 =(0,2
=(0,2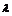 ,
,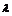 -2)·(0,2,1)=5
-2)·(0,2,1)=5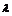 -2=0,
-2=0,
解得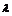 =
=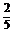 .
.
故当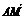 =
=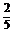
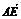 时,A1M⊥平面ADE.
时,A1M⊥平面ADE.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com