
6.(2009·宁夏高考)水平地面上有一木箱,木箱与地面之间的动摩擦因数为μ(0<μ<1).现
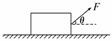 对木箱施加一拉力F,使木箱做匀速直线运动.设F的方向与水
对木箱施加一拉力F,使木箱做匀速直线运动.设F的方向与水
 平面夹角为θ,如图5所示,在θ从0逐渐增大到90°的过程中,木
平面夹角为θ,如图5所示,在θ从0逐渐增大到90°的过程中,木
箱的速度保持不变,则 ( )
A.F先减小后增大 B.F一直增大
C.F的功率减小 D.F的功率不变
解析:由木箱受力平衡可知:Fcosθ=μ(G-Fsinθ),
即F==,
故F先减小后变大.根据P=Fvcosθ=可知F的功率减小.故A、C正确.
答案:AC
5. (2010·常州模拟)如图3所示,质量为m的物体置于水平地面上,所受水平拉力F在2
s时间内的变化图象如图4甲所示,其运动的速度图象如图4乙所示,g=10
m/s2.下列说法正确的是
( ) 图3
(2010·常州模拟)如图3所示,质量为m的物体置于水平地面上,所受水平拉力F在2
s时间内的变化图象如图4甲所示,其运动的速度图象如图4乙所示,g=10
m/s2.下列说法正确的是
( ) 图3

图4
A.物体和地面之间的动摩擦因数为0.1
B.水平拉力F的最大功率为5 W
C.2 s 末物体回到出发点
D.2 s 内物体的加速度不变
解析:本题考查通过图象处理匀变速运动问题.在减速阶段,Ff=ma,μmg=ma,μ=0.1,A正确;拉力F的最大功率P=Fv=10×1 W=10 W,B不正确;物体在第一秒内受到的合力的方向与第二秒内受到的合力的方向相反,加速度方向相反,D不正确;由v-t图象可知,物体在2 s 内位移是速度图线与t轴所围面积,即1 m,没有回到起点,C不正确.
答案:A
4.(2008·宁夏高考)一滑块在水平地面上沿直线滑行,t=0时其速度为1 m/s,从此刻开始在滑块运动方向上再施加一水平作用力F,力F和滑块的速率v随时间的变化规律分别如图2甲和乙所示.设在第1秒内、第2秒内、第3秒内力F对滑块做的功分别为W1、W2、W3,则以下关系正确的是 ( )
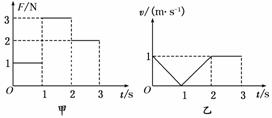
图2
A.W1=W2=W3 B.W1<W2<W3
C.W1<W3<W2 D.W1=W2<W3
解析:力F做的功等于每段恒力F与该段滑块运动的位移数值(v-t图象中图象与坐标轴围成的面积)的乘积,第1秒内,位移为一个小三角形面积S;第2秒内,位移也为一个小三角形面积S;第3秒内,位移为两个小三角形面积2S,故W1=1S,W2=3S,W3=4S,所以W1<W2<W3.
答案:B
3. (2010·苏州模拟)如图1所示,质量相同的两物体处于同一高度,A沿固定在地面上的
(2010·苏州模拟)如图1所示,质量相同的两物体处于同一高度,A沿固定在地面上的

光滑斜面下滑,B自由下落,最后到达同一水平面,则 ( )
A.重力对两物体做的功相同
B.重力的平均功率相同
C.到达底端时重力的瞬时功率相同
D.到达底端时两物体的动能相同,速度相同
解析:由于两个物体质量相同、下落高度相同,所以重力对两物体做的功相同,A选项正确.由于下落的时间不同,所以重力的平均功率不相同,B选项错误.根据机械能守恒可知,两物体到达底端时动能相同,即速度大小相同、方向不同,D选项错误.由瞬时功率的计算式可得PA=mgvcosθ,PB=mgv,因此,到达底端时重力的瞬时功率PA<PB,C选项错误.
答案:A
2.在距地面高5 m的平台上,以25 m/s的速率竖直向上抛出一质量为1 kg的石块,不计空气阻力,取g=10 m/s2,则抛出后第三秒内重力对石块所做的功是 ( )
A.-100 J B.50 J
C.100 J D.0 J
解析:石块在2 s末与3 s末在同一位置,故第3 s内位移为0,所以第3 s内重力做功为
零.
答案:D
1.一人乘电梯从1楼到20楼,在此过程中经历了先加速,后匀速,再减速的运动过程,则电梯支持力对人做功情况是 ( )
A.加速时做正功,匀速时不做功,减速时做负功
B.加速时做正功,匀速和减速时做负功
C.加速和匀速时做正功,减速时做负功
D.始终做正功
解析:支持力始终竖直向上,与位移同向,α=0°,故支持力始终做正功,D正确.
答案:D
12.已知向量a= ,x∈
,x∈ .若函数f(x)=a·b-
.若函数f(x)=a·b-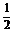
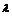 |a+b|的最小值为-
|a+b|的最小值为- ,求实数
,求实数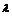 的值.
的值.
解 ∵|a|=1,|b|=1,x∈ ,
,
∴a·b=cos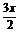 cos
cos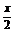 -sin
-sin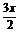 sin
sin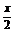 =cos2x,
=cos2x,
|a+b|=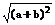 =
=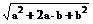
=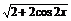 =2
=2 =2cosx.
=2cosx.
∴f(x)=cos2x-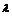 cosx=2cos2x-
cosx=2cos2x-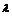 cosx-1
cosx-1
=2 -
-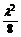 -1,cosx∈[0,1].
-1,cosx∈[0,1].
①当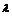 <0时,取cosx=0,此时f(x)取得最小值,
<0时,取cosx=0,此时f(x)取得最小值,
并且f(x)min=-1≠- ,不合题意.
,不合题意.
②当0≤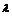 ≤4时,取cosx=
≤4时,取cosx= ,
,
此时f(x)取得最小值,
并且f(x)min=-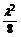 -1=-
-1=- ,解得
,解得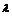 =2.
=2.
③当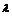 >4时,取cosx=1,此时f(x)取得最小值,
>4时,取cosx=1,此时f(x)取得最小值,
并且f(x)min=1-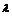 =-
=- ,
,
解得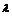 =
= ,不符合
,不符合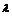 >4舍去,∴
>4舍去,∴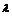 =2.
=2.
11.设n和m是两个单位向量,其夹角是60°,求向量a=2m+n与b=2n-3m的夹角.
解 由|m|=1,|n|=1,夹角为60°,得m·n=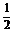 .
.
则有|a|=|2m+n|=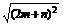 =
=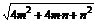 =
=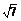 .
.
|b|=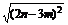 =
=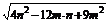 =
=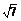 .
.
而a·b=(2m+n)·(2n-3m)=m·n-6m2+2n2=- ,
,
设a与b的夹角为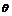 ,
,
则cos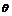 =
=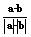 =
= =-
=-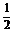 .故a,b夹角为120°.
.故a,b夹角为120°.
10.已知a=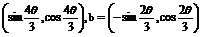 ,且
,且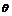 ∈
∈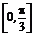 .
.
(1)求 的最值;
的最值;
(2)若|ka+b|= |a-kb| (k∈R),求k的取值范围.
|a-kb| (k∈R),求k的取值范围.
解 (1)a·b=-sin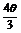 ·sin
·sin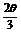 +cos
+cos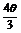 ·cos
·cos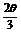 =cos2
=cos2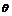 ,
,
|a+b|2=|a|2+|b|2+2a·b=2+2cos2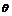 =4cos2
=4cos2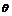 .
.
∵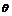 ∈
∈ ,∴cos
,∴cos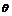 ∈
∈ ,∴|a+b|=2cos
,∴|a+b|=2cos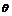 .
.
∴ =
= 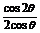 =cos
=cos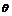 -
-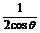 .
.
令t=cos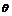 ,则
,则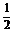 ≤t≤1,
≤t≤1, ′=1+
′=1+ >0,
>0,
∴t- 在t∈
在t∈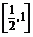 上为增函数.
上为增函数.
∴-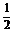 ≤t-
≤t- ≤
≤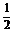 ,
,
即所求式子的最大值为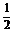 ,最小值为-
,最小值为-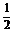 .
.
(2)由题设可得|ka+b|2=3|a-kb|2,
∴(ka+b)2=3(a-kb)2
又|a|=|b|=1,a·b=cos2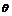 ,∴cos2
,∴cos2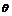 =
=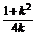 .
.
由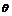 ∈
∈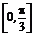 ,得-
,得-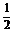 ≤cos2
≤cos2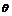 ≤1.
≤1.
∴-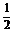 ≤
≤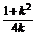 ≤1.解得k∈[2-
≤1.解得k∈[2- ,2+
,2+ ]
] {-1}.
{-1}.
9.已知平面上三个向量a、b、c的模均为1,它们相互之间的夹角均为120°.
(1)求证:(a-b)⊥c;
(2)若|ka+b+c|>1 (k∈R),求k的取值范围.
(1)证明 ∵(a-b)·c=a·c-b·c
=|a|·|c|·cos120°-|b|·|c|·cos120°=0,
∴(a-b)⊥c.
(2)解 |ka+b+c|>1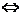 |ka+b+c|2>1,
|ka+b+c|2>1,
?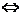 k2a2+b2+c2+2ka·b+2ka·c+2b·c>1.
k2a2+b2+c2+2ka·b+2ka·c+2b·c>1.
∵|a|=|b|=|c|=1,且a、b、c的夹角均为120°,
∴a2=b2=c2=1,a·b=b·c=a·c=-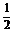 ,
,
∴k2+1-2k>1,即k2-2k>0,∴k>2或k<0.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com