
22.(14分)已知函数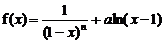 ,其中n∈N+,
,其中n∈N+, 为常数。
为常数。
①当n=2时,求函数f(x)的极值;
②当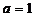 时,证明:对任意的正整数n,当x≥2时,
时,证明:对任意的正整数n,当x≥2时,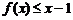 。
。



21.(12分)已知二次函数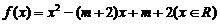 ,同时满足:①不等式
,同时满足:①不等式 的解集有且只有一个元素;②在定义域内存在x1、x2,使得x1+x2=0,但f(x1) ≠f(x2),设数列
的解集有且只有一个元素;②在定义域内存在x1、x2,使得x1+x2=0,但f(x1) ≠f(x2),设数列 的前n项和Sn=f(n)。
的前n项和Sn=f(n)。
①求f(x)的表达式;
②求数列 的通项公式。
的通项公式。
③若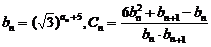 ,数列
,数列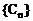 的前n项和为Tn
,Tn>n+m,对n∈N+,n≥2恒成立,求m的范围。
的前n项和为Tn
,Tn>n+m,对n∈N+,n≥2恒成立,求m的范围。
20.(12分)设F1、F2分别是椭圆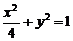 的左、右焦点。
的左、右焦点。
①若P是该椭圆上的一个动点,求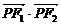 的最大值和最小值;
的最大值和最小值;
②设过定点M(0,2)的直线L与椭圆交于不同的两点A、B,且∠AOB为锐角(其中O为坐标原点),求直线L的斜率k的取值范围。
19.(12分)如图,正三棱柱ABC-A1B1C1中,D是BC的中点,AA1=AB=1.
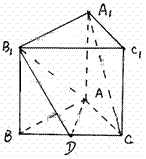 ①求证:A1C∥平面AB1D;
①求证:A1C∥平面AB1D;
②求二面角B-AB1-D的大小;
③求点C到平面AB1D的距离。
18.(12分)有甲、乙、丙、丁四名乒乓球运动员,通过对他们过去成绩的统计,在一场比赛中,甲对乙、丙、丁,甲取胜的概率分别为0.6、0.8、0.9。
①若四名运动员每两人之间进行一场比赛,求甲恰好取胜两场的概率;
②若四名运动员每两人之间进行一场比赛,设甲获胜场次为ξ,求随机变量ξ的分布列及期望Eξ。
17.(12分)已知0是坐标原点,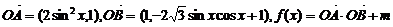 ,
,
①求f(x)的单调递增区间;
②若f(x)的定义域为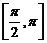 ,值域为[2,5],求m的值。
,值域为[2,5],求m的值。
16.已知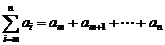 (其中m,n∈Z且0≤m<n),设
(其中m,n∈Z且0≤m<n),设  ,函数
,函数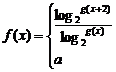
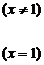 ,在x=1处连续,则实数a的值_______________
,在x=1处连续,则实数a的值_______________
15.已知 ,则
,则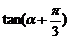 =_______________
=_______________
14.已知数列{an}是二项式(2+3x)n(n≥2,n∈N+) 展开式的第3项的二项式系数,Sn是数列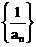 的前n项和,则
的前n项和,则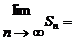 _______________
_______________
13.“x>1”是“x2>1”的_______________条件。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com