
2.集合 ,从A到B的映射f满足
,从A到B的映射f满足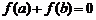 ,那么这样的映射
,那么这样的映射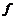
的个数有( )
A.2个 B.3个 C.5个 D.8个
1.设a,b为实数,若复数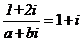 ,则
,则
A.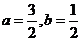 B.
B. 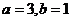 C.
C. 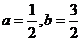
 D.
D. 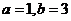
反函数的定义及其注意点、求法步骤
(1)
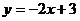 (x∈R) (2)
(x∈R) (2)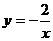 (x∈R,且x≠0)
(x∈R,且x≠0)
(3)
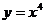 (x≥0) (4)
(x≥0) (4)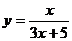 (x∈R,且x≠
(x∈R,且x≠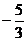 )
)
例1.求下列函数的反函数:
①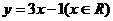 ;
②
;
②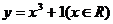 ;
;
③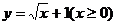 ; ④
; ④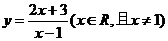 .
.
解:①由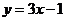 解得
解得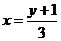
∴函数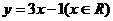 的反函数是
的反函数是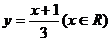 ,
,
②由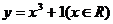 解得x=
解得x=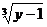 ,
,
∴函数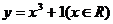 的反函数是
的反函数是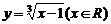
③由y=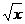 +1解得x=
+1解得x= ,
,
∵x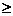 0,∴y
0,∴y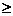 1.
1.
∴函数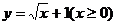 的反函数是x=
的反函数是x= (x
(x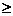 1);
1);
④由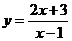 解得
解得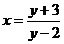
∵xc{x R|x
R|x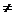 1},∴y
1},∴y {y
{y R|y
R|y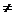 2}
2}
∴函数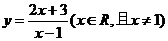 的反函数是
的反函数是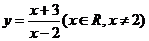
小结:⑴求反函数的一般步骤分三步,一解、二换、三注明
⑵反函数的定义域由原来函数的值域得到,而不能由反函数的解析式得到
⑶求反函数前先判断一下决定这个函数是否有反函数,即判断映射是否是一一映射
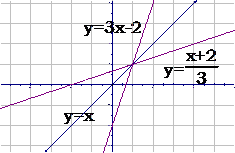
例2.求函数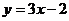 (
(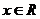 )的反函数,并画出原来的函数和它的反函数的图像
)的反函数,并画出原来的函数和它的反函数的图像
解:由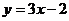 解得
解得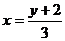
 ∴函数
∴函数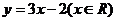 的反函数是
的反函数是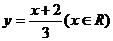 ,
,
它们的图像为:
例3求函数 
(-1<x<0)的反函数
解:∵ -1<x<0 ∴0<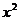 <1 ∴0<1 -
<1 ∴0<1 -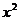 < 1
< 1
∴
0 <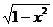 < 1 ∴0 < y <1
< 1 ∴0 < y <1
由: 解得:
解得: (∵ -1< x < 0 )
(∵ -1< x < 0 )
∴ (-1<x < 0)的反函数是:
(-1<x < 0)的反函数是: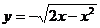 (0<x<1 )
(0<x<1 )
例4 已知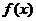 =
= 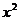 -2x(x≥2),求
-2x(x≥2),求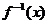 .
.
解法1:⑴令y=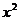 -2x,解此关于x的方程得
-2x,解此关于x的方程得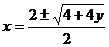 ,
,
∵x≥2,∴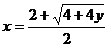 ,即x=1+
,即x=1+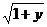 --①,
--①,
⑵∵x≥2,由①式知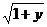 ≥1,∴y≥0--②,
≥1,∴y≥0--②,
⑶由①②得 =1+
=1+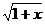 (x≥0,x∈R);
(x≥0,x∈R);
解法2:⑴令y=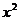 -2x=
-2x=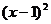 -1,∴
-1,∴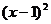 =1+y,
=1+y,
∵x≥2,∴x-1≥1,∴x-1=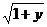 --①,即x=1+
--①,即x=1+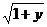 ,
,
⑵∵x≥2,由①式知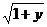 ≥1,∴y≥0,
≥1,∴y≥0,
⑶∴函数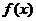 =
= 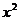 -2x(x≥2)的反函数是
-2x(x≥2)的反函数是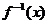 =1+
=1+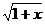 (x≥0);
(x≥0);
说明:二次函数在指定区间上的反函数可以用求根公式反求x,也可以用配方法求x,但开方时必须注意原来函数的定义域.
反函数的定义
一般地,设函数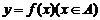 的值域是C,根据这个函数中x,y 的关系,用y把x表示出,得到x=
的值域是C,根据这个函数中x,y 的关系,用y把x表示出,得到x=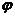 (y). 若对于y在C中的任何一个值,通过x=
(y). 若对于y在C中的任何一个值,通过x=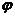 (y),x在A中都有唯一的值和它对应,那么,x=
(y),x在A中都有唯一的值和它对应,那么,x=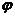 (y)就表示y是自变量,x是自变量y的函数,这样的函数x=
(y)就表示y是自变量,x是自变量y的函数,这样的函数x=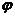 (y) (y
(y) (y C)叫做函数
C)叫做函数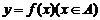 的反函数,记作
的反函数,记作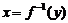 ,习惯上改写成
,习惯上改写成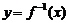
开始的两个例子:s=vt记为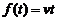 ,则它的反函数就可以写为
,则它的反函数就可以写为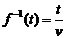 ,同样
,同样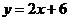 记为
记为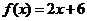 ,则它的反函数为:
,则它的反函数为: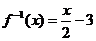 .
.
探讨1:所有函数都有反函数吗?为什么?
反函数也是函数,因为它符合函数的定义,从反函数的定义可知,对于任意一个函数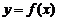 来说,不一定有反函数,如
来说,不一定有反函数,如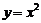 ,只有“一一映射”确定的函数才有反函数,
,只有“一一映射”确定的函数才有反函数,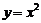 ,
,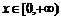 有反函数是
有反函数是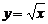
探讨2:互为反函数定义域、值域的关系
从映射的定义可知,函数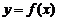 是定义域A到值域C的映射,而它的反函数
是定义域A到值域C的映射,而它的反函数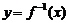 是集合C到集合A的映射,因此,函数
是集合C到集合A的映射,因此,函数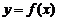 的定义域正好是它的反函数
的定义域正好是它的反函数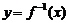 的值域;函数
的值域;函数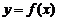 的值域正好是它的反函数
的值域正好是它的反函数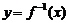 的定义域
的定义域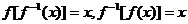 (如下表):
(如下表):
|
|
函数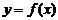 |
反函数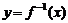 |
|
定义域 |
A |
C |
|
值 域 |
C |
A |
探讨3: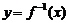 的反函数是?
的反函数是?
若函数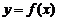 有反函数
有反函数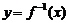 ,那么函数
,那么函数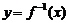 的反函数就是
的反函数就是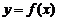 ,这就是说,函数
,这就是说,函数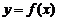 与
与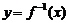 互为反函数
互为反函数
我们知道,物体作匀速直线运动的位移s是时间t的函数,即s=vt,其中速度v是常量,定义域t 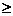 0,值域s
0,值域s 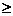 0;反过来,也可以由位移s和速度v(常量)确定物体作匀速直线运动的时间,即
0;反过来,也可以由位移s和速度v(常量)确定物体作匀速直线运动的时间,即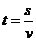 ,这时,位移s是自变量,时间t是位移s的函数,定义域s
,这时,位移s是自变量,时间t是位移s的函数,定义域s 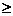 0,值域t
0,值域t 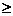 0.
0.
又如,在函数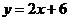 中,x是自变量,y是x的函数,定义域x
中,x是自变量,y是x的函数,定义域x R,值域y
R,值域y R. 我们从函数
R. 我们从函数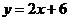 中解出x,就可以得到式子
中解出x,就可以得到式子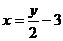 . 这样,对于y在R中任何一个值,通过式子
. 这样,对于y在R中任何一个值,通过式子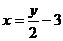 ,x在R中都有唯一的值和它对应. 因此,它也确定了一个函数:y为自变量,x为y的函数,定义域是y
,x在R中都有唯一的值和它对应. 因此,它也确定了一个函数:y为自变量,x为y的函数,定义域是y R,值域是x
R,值域是x R.
R.
综合上述,我们由函数s=vt得出了函数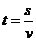 ;由函数
;由函数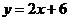 得出了函数
得出了函数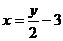 ,不难看出,这两对函数中,每一对中两函数之间都存在着必然的联系:①它们的对应法则是互逆的;②它们的定义域和值域相反:即前者的值域是后者的定义域,而前者的定义域是后者的值域. 我们称这样的每一对函数是互为反函数.
,不难看出,这两对函数中,每一对中两函数之间都存在着必然的联系:①它们的对应法则是互逆的;②它们的定义域和值域相反:即前者的值域是后者的定义域,而前者的定义域是后者的值域. 我们称这样的每一对函数是互为反函数.
28.(1)材料一、二两种治国思想的不同点?(2分)
(2)材料三、四两种主张的共同之处是什么?差别又在哪里?实施结果如何?(10分)
(3)几则材料折射出此间中国古代思想领域呈现怎样的发展趋势?分别反映了哪些实质性问题?(4分)
27.(1)概括两汉与宋代教育的共同特点,相对于封建官学,书院教学的有哪些优势?(7分)
(2)明清时期江南教育较前代出现哪些变化?分析的变化原因?(10分)
26.(1)材料二与材料一对比,相同的主张是什么?适应了怎样的时代要求?(5分)
(2)材料二比材料一又有哪些重要发展,其积极意义何在?(6分)
(3)黄宗羲对中国提出了怎样的政治设计? 这种设计的历史缺陷何在?造成这种缺陷的根本原因是什么? (6分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com