
15.(本小题满分14分)
设向量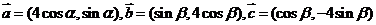

(1)若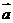 与
与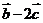 垂直,求
垂直,求 的值;
的值;
(2)求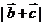 的最大值;
的最大值;
(3)若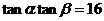 ,求证:
,求证: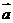 ∥
∥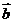 .
. .网
.网
[解析] 本小题主要考查向量的基本概念,同时考查同角三角函数的基本关系式、二倍角的正弦、两角和的正弦与余弦公式,考查运算和证明得基本能力。满分14分。
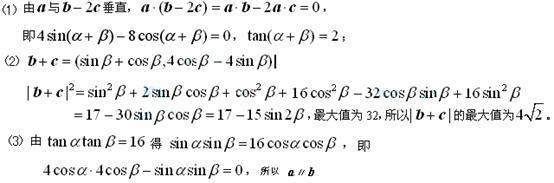
14.设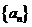 是公比为
是公比为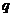 的等比数列,
的等比数列,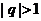 ,令
,令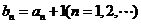 ,若数列
,若数列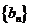 有连续四项在集合
有连续四项在集合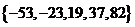 中,则
中,则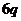 = ▲ .
= ▲ .
[解析] 考查等价转化能力和分析问题的能力。等比数列的通项。
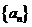 有连续四项在集合
有连续四项在集合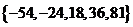 ,四项
,四项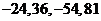 成等比数列,公比为
成等比数列,公比为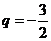 ,
,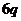 = -9
= -9
13.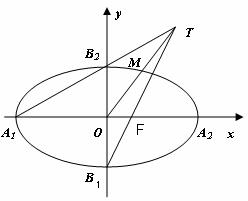 如图,在平面直角坐标系
如图,在平面直角坐标系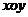 中,
中,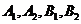 为椭圆
为椭圆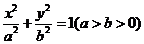 的四个顶点,
的四个顶点,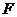 为其右焦点,直线
为其右焦点,直线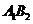 与直线
与直线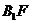 相交于点T,线段
相交于点T,线段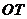 与椭圆的交点
与椭圆的交点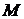 恰为线段
恰为线段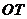 的中点,则该椭圆的离心率为
▲ .
的中点,则该椭圆的离心率为
▲ .


[解析] 考查椭圆的基本性质,如顶点、焦点坐标,离心率的计算等。以及直线的方程。
直线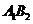 的方程为:
的方程为: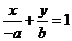 ;
;
直线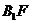 的方程为:
的方程为: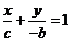 。二者联立解得:
。二者联立解得: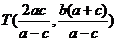 ,
,
则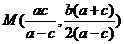 在椭圆
在椭圆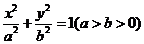 上,
上,
 ,
,
解得: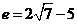
12.设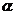 和
和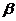 为不重合的两个平面,给出下列命题:
为不重合的两个平面,给出下列命题:
(1)若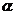 内的两条相交直线分别平行于
内的两条相交直线分别平行于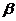 内的两条直线,则
内的两条直线,则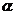 平行于
平行于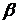 ;
;
(2)若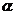 外一条直线
外一条直线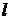 与
与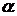 内的一条直线平行,则
内的一条直线平行,则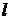 和
和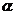 平行;
平行;
(3)设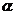 和
和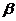 相交于直线
相交于直线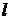 ,若
,若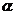 内有一条直线垂直于
内有一条直线垂直于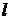 ,则
,则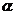 和
和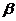 垂直;
垂直;
(4)直线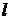 与
与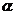 垂直的充分必要条件是
垂直的充分必要条件是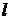 与
与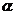 内的两条直线垂直。
内的两条直线垂直。
上面命题中,真命题的序号 ▲ (写出所有真命题的序号).
[解析] 考查立体几何中的直线、平面的垂直与平行判定的相关定理。
真命题的序号是(1)(2)
11.已知集合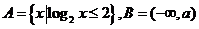 ,若
,若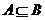 则实数
则实数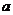 的取值范围是
的取值范围是 ,其中
,其中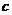 = ▲ .
= ▲ .
[解析] 考查集合的子集的概念及利用对数的性质解不等式。
由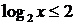 得
得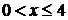 ,
,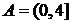 ;由
;由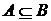 知
知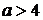 ,所以
,所以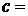 4。
4。
10.已知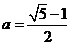 ,函数
,函数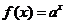 ,若实数
,若实数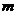 、
、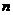 满足
满足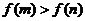 ,则
,则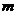 、
、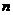 的大小关系为 ▲ .
的大小关系为 ▲ .
[解析] 考查指数函数的单调性。
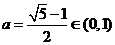 ,函数
,函数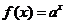 在R上递减。由
在R上递减。由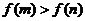 得:m<n
得:m<n
9.在平面直角坐标系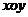 中,点P在曲线
中,点P在曲线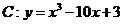 上,且在第二象限内,已知曲线C在点P处的切线的斜率为2,则点P的坐标为 ▲ .
上,且在第二象限内,已知曲线C在点P处的切线的斜率为2,则点P的坐标为 ▲ .
[解析] 考查导数的几何意义和计算能力。
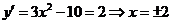 ,又点P在第二象限内,
,又点P在第二象限内,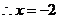
点P的坐标为(-2,15)
8.在平面上,若两个正三角形的边长的比为1:2,则它们的面积比为1:4,类似地,在空间内,若两个正四面体的棱长的比为1:2,则它们的体积比为 ▲ .
[解析] 考查类比的方法。
体积比为1:8
7.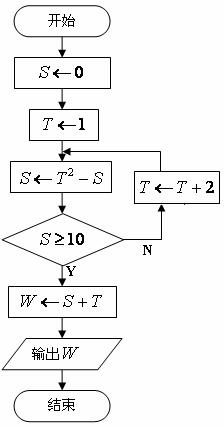 右图是一个算法的流程图,最后输出的
右图是一个算法的流程图,最后输出的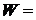 ▲ .
▲ .
[解析] 考查读懂算法的流程图的能力。
22
6.某校甲、乙两个班级各有5名编号为1,2,3,4,5的学生进行投篮练习,每人投10次,投中的次数如下表:
|
学生 |
1号 |
2号 |
3号 |
4号 |
5号 |
|
甲班 |
6 |
7 |
7 |
8 |
7 |
|
乙班 |
6 |
7 |
6 |
7 |
9 |
则以上两组数据的方差中较小的一个为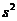 = ▲ .
= ▲ .
[解析] 考查统计中的平均值与方差的运算。
甲班的方差较小,数据的平均值为7,
故方差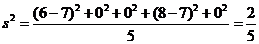
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com