
7. (2008贵州贵阳)利用图像解一元二次方程
(2008贵州贵阳)利用图像解一元二次方程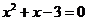 时,我们采用的一种方法是:在平面直角坐标系中画出抛物线
时,我们采用的一种方法是:在平面直角坐标系中画出抛物线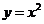 和直线
和直线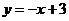 ,两图像交点的横坐标就是该方程的解.
,两图像交点的横坐标就是该方程的解.
(1)填空:利用图像解一元二次方程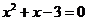 ,也可以这样求解:在平面直角坐标系中画出抛物线
,也可以这样求解:在平面直角坐标系中画出抛物线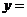 和直线
和直线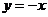 ,其交点的横坐标就是该方程的解.(4分)
,其交点的横坐标就是该方程的解.(4分)
(2)已知函数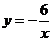 的图像(如图9所示),利用图像求方程
的图像(如图9所示),利用图像求方程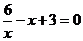 的近似解(结果保留两个有效数字).(6分)
的近似解(结果保留两个有效数字).(6分)
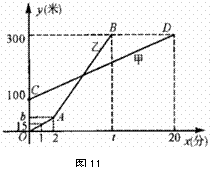
5.(2008湖北鄂州)甲乙两人同时登西山,甲、乙两人距地面的高度 (米)与登山时间
(米)与登山时间 (分)之间的函数图象如图11所示,根据图象所提供的信息解答下列问题:
(分)之间的函数图象如图11所示,根据图象所提供的信息解答下列问题:
(1)甲登山的速度是每分钟 米,
乙在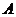 地提速时距地面的高度
地提速时距地面的高度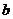 为
米.
为
米.
 (2)若乙提速后,乙的速度是甲登山速度的3倍,请分别求出甲、乙二人登山全过程中,登山时距地面的高度
(2)若乙提速后,乙的速度是甲登山速度的3倍,请分别求出甲、乙二人登山全过程中,登山时距地面的高度 (米)与登山时间
(米)与登山时间 (分)之间的函数关系式.
(分)之间的函数关系式.
(3)登山多长时间时,乙追上了甲?此时乙距 地的高度为多少米?
地的高度为多少米?
4.(2008 河南)复习“全等三角形”的知识时,老师布置了一道作业题:
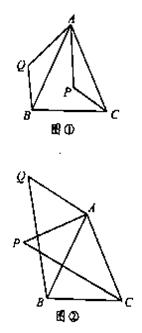
“如图①,已知,在△ABC中,AB=AC,P是△ABC中内任意一点,将AP绕点A
顺时针旋转至AQ,使∠QAP=∠BAC,连结BQ、CP则BQ=CP。”
小亮是个爱动脑筋的同学,他通过对图①的分析,证明了△ABC≌△ACP,从而证得BQ=CP。之后,他将点P移到等腰三角形ABC外,原题中其它条件不变,发现“BQ=CP” 仍然成立,请你就图②给出证明。
3.(2008 湖南 益阳)△ABC是一块等边三角形的废铁片,利用其剪裁一个正方形DEFG,使正方形的一条边DE落在BC上,顶点F、G分别落在AC、AB上.
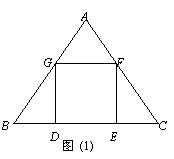 Ⅰ.证明:△BDG≌△CEF;
Ⅰ.证明:△BDG≌△CEF;
Ⅱ. 探究:怎样在铁片上准确地画出正方形.
小聪和小明各给出了一种想法,请你在Ⅱa和Ⅱb的两个问题中选择一个你喜欢的问题解答. 如果两题都解,只以Ⅱa的解答记分.
Ⅱa. 小聪想:要画出正方形DEFG,只要能计算出正方形的边长就能求出BD和CE的长,从而确定D点和E点,再画正方形DEFG就容易了.
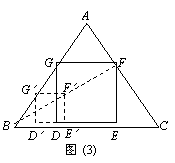 设△ABC的边长为2 ,请你帮小聪求出正方形的边长(结果用含根号的式子表示,不要求分母有理化) .
设△ABC的边长为2 ,请你帮小聪求出正方形的边长(结果用含根号的式子表示,不要求分母有理化) .
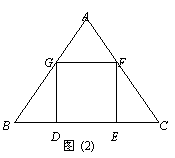
Ⅱb. 小明想:不求正方形的边长也能画出正方形. 具体作法是:
①在AB边上任取一点G’,如图作正方形G’D’E’F’;
②连结BF’并延长交AC于F;
③作FE∥F’E’交BC于E,FG∥F′G′交AB于G,GD∥G’D’交BC于D,则四边形DEFG即为所求.
你认为小明的作法正确吗?说明理由.
2. (2008 河北)在一平直河岸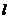 同侧有
同侧有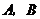 两个村庄,
两个村庄,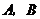 到
到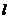 的距离分别是3km和2km,
的距离分别是3km和2km,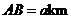
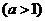 .现计划在河岸
.现计划在河岸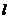 上建一抽水站
上建一抽水站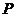 ,用输水管向两个村庄供水.
,用输水管向两个村庄供水.
方案设计
某班数学兴趣小组设计了两种铺设管道方案:图1是方案一的示意图,设该方案中管道长度为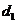 ,且
,且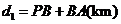 (其中
(其中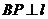 于点
于点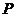 );图2是方案二的示意图,设该方案中管道长度为
);图2是方案二的示意图,设该方案中管道长度为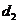 ,且
,且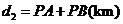 (其中点
(其中点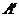 与点
与点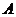 关于
关于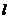 对称,
对称,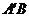 与
与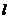 交于点
交于点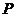 ).
).

观察计算
(1)在方案一中, km(用含
km(用含 的式子表示);
的式子表示);
(2)在方案二中,组长小宇为了计算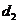 的长,作了如图3所示的辅助线,请你按小宇同学的思路计算,
的长,作了如图3所示的辅助线,请你按小宇同学的思路计算,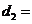 km(用含
km(用含 的式子表示).
的式子表示).
探索归纳
(1)①当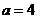 时,比较大小:
时,比较大小: (填“>”、“=”或“<”);
(填“>”、“=”或“<”);
②当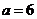 时,比较大小:
时,比较大小: (填“>”、“=”或“<”);
(填“>”、“=”或“<”);
(2)请你参考右边方框中的方法指导,
就 (当
(当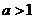 时)的所有取值情况进
时)的所有取值情况进
行分析,要使铺设的管道长度较短,
应选择方案一还是方案二?


1. (2008年山东省滨州市)(1)探究新知:
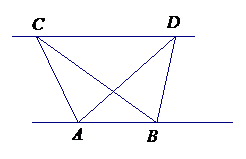
如图1,已知△ABC与△ABD的面积相等,试判断AB与CD的位置关系,并说明理由.
(2)结论应用:
①如图2,点M、N在反比例函数y=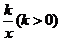 的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F.
的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F.
试应用(1)中得到的结论证明:MN∥EF.
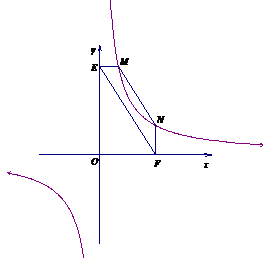
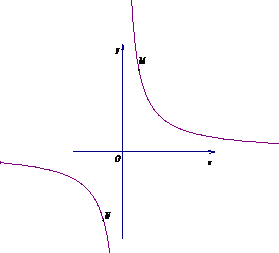
②若①中的其他条件不变,只改变点M,N的位置如图3所示,
请判断MN与E是否平行.
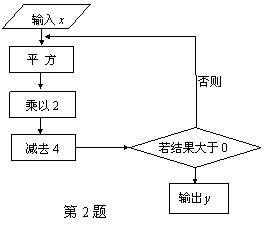
2.(2008湖南株洲)根据如上图所示的程序计算,若输入的x的值为1,则输出的y值为 .
6.(2008浙江湖州)解放军某部接到上级命令,乘车前往四川地震灾区救灾,前进一段路程后,由于道路受阻,汽车无法通行,部队通过短暂休整后决定步行前往,若部队离开驻地的时间为t(小时),离开驻地的距离为S(千米),则能反映S与t之间函数关系的大致图象是( )
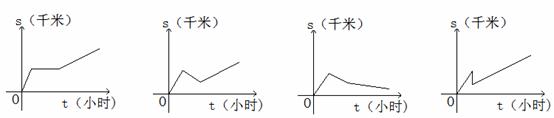
A B C D
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com