
1.(2008年广东卷,数学理科,5,数学文科,7)将正三棱柱截去三个角(如图1所示 分别是
分别是 三边的中点)得到几何体如图2,则该几何体按图2所示方向的侧视图(或称左视图)为(
)
三边的中点)得到几何体如图2,则该几何体按图2所示方向的侧视图(或称左视图)为(
)


[解析]本题考查几何体的三视图,解题时在图2的右边放扇墙(心中有墙),可得答案.
[答案]A
09考试大纲中,对本节的要求如下:
(1)空间几何体
① 认识柱、锥、台、球及其简单组合体的结构特征,并能运用这些特征描述现实生活中简单物体的结构.
② 能画出简单空间图形(长方体、球、圆柱、圆锥、棱柱等的简易组合)的三视图,能识别上述的三视图所表示的立体模型,会用斜二测法画出它们的直观图.
③ 会用平行投影与中心投影两种方法,画出简单空间图形的三视图与直观图,了解空间图形的不同表示形式.
④ 会画某些建筑物的视图与直观图(在不影响图形特征的基础上,尺寸、线条等不作严格要求).
⑤ 了解球、棱柱、棱锥、台的表面积和体积的计算公式(不要求记忆公式).
(2)点、直线、平面之间的位置关系
① 理解空间直线、平面位置关系的定义,并了解如下可以作为推理依据的公理和定理.
◆公理1:如果一条直线上的两点在一个平面内,那么这条直线上所有的点在此平面内.
◆公理2:过不在同一条直线上的三点,有且只有一个平面.
◆公理3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.
◆公理4:平行于同一条直线的两条直线互相平行.
◆定理:空间中如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补.
② 以立体几何的上述定义、公理和定理为出发点,认识和理解空间中线面平行、垂直的有关性质与判定定理.
理解以下判定定理.
◆如果平面外一条直线与此平面内的一条直线平行,那么该直线与此平面平行.
◆如果一个平面内的两条相交直线与另一个平面都平行,那么这两个平面平行.
◆如果一条直线与一个平面内的两条相交直线都垂直,那么该直线与此平面垂直.
◆如果一个平面经过另一个平面的垂线,那么这两个平面互相垂直.
理解以下性质定理,并能够证明.
◆如果一条直线与一个平面平行,经过该直线的任一个平面与此平面相交,那么这条直线就和交线平行.
◆如果两个平行平面同时和第三个平面相交,那么它们的交线相互平行.
◆垂直于同一个平面的两条直线平行.
◆如果两个平面垂直,那么一个平面内垂直于它们交线的直线与另一个平面垂直.
③ 能运用公理、定理和已获得的结论证明一些空间图形的位置关系的简单命题.
2.08届莆田四中5月份第2次模拟试卷(本小题满分12分)已知,如图四棱锥 中,底面
中,底面 是平行四边形,
是平行四边形, ,垂足
,垂足 在
在 上,且
上,且 ,
, ,
, ,
, ,
, 是
是 的中点.
的中点.
 (1)求异面直线
(1)求异面直线 与
与 所成的角;
所成的角;
 (2)求点
(2)求点 到平面
到平面 的距离;
的距离;
(3)若 点是棱
点是棱 上一点,且
上一点,且 ,求
,求 的值.
的值.
解法一:(1)在平面 内,过
内,过 点作
点作 交
交 于
于 ,连结
,连结 ,
,
则 (或其补角)就是异面直线
(或其补角)就是异面直线 与
与 所成的角.
所成的角.
 在
在 中,
中, ,
,
由余弦定理得, =
=
∴异面直线 与
与 所成的角为arccos
所成的角为arccos
(2)∵ 平面
平面 ,
, 平面
平面 ∴平面
∴平面 ⊥平面
⊥平面
在平面 内,过
内,过 作
作 ,交
,交 延长线于
延长线于 ,则
,则 ⊥平面
⊥平面
∴ 的长就是点
的长就是点 到平面
到平面 的距离
的距离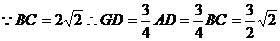
在 ,
, ∴点
∴点 到平面
到平面 的距离为
的距离为
(3)在平面 内,过
内,过 作
作 ,
, 为垂足,连结
为垂足,连结 ,又因为
,又因为
∴ 平面
平面 ,
∴
,
∴
由平面 ⊥平面
⊥平面 ,∴
,∴ ⊥平面
⊥平面 ∴
∴
由 得:
得:


解法二:(1)由已知 ∴
∴
如图所示,以G点为原点建立空间直角坐标系o-xyz,则
 ,
, ,
, 故
故

∴异面直线 与
与 所成的角为arccos
所成的角为arccos 4分
4分
(2)平面PBG的单位法向量

∴点 到平面
到平面 的距离为
的距离为 ------------- 8分
------------- 8分
(3)设

在平面 内过
内过 点作
点作 ,
, 为垂足,则
为垂足,则
 ------------- 12分
------------- 12分

2. 宁夏银川一中2008届高三年级第三次模拟考试
宁夏银川一中2008届高三年级第三次模拟考试
(本小题共12分)
在三棱锥 中,
中, ,
,
 .
.
(Ⅰ)证明: ⊥
⊥ ;
;
(Ⅱ)求二面角A-BC-S的大小;
(Ⅲ)求直线AB与平面SBC所成角的正弦值.
解法一:
解:(Ⅰ) 且
且 平面
平面 .-------------2分
.-------------2分
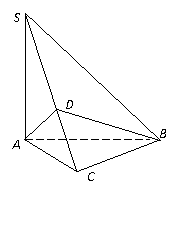
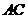 为
为 在平面
在平面 内的射影.
--------3分
内的射影.
--------3分
又 ⊥
⊥ , ∴
, ∴ ⊥
⊥ .
----------4分
.
----------4分
(Ⅱ) 由(Ⅰ) ⊥
⊥ ,又
,又 ⊥
⊥ ,
,
∴ 为所求二面角的平面角.
-------6分
为所求二面角的平面角.
-------6分
又∵ =
=
 =4,
=4,
∴ =4 . ∵
=4 . ∵ =2 , ∴
=2 , ∴ =60°. -------8分
=60°. -------8分
即二面角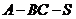 大小为60°.
大小为60°.
(Ⅲ)过 作
作 于D,连结
于D,连结 ,
,
由(Ⅱ)得平面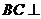 平面
平面 ,又
,又
 平面
平面 ,
,
∴平面
 平面
平面 ,且平面
,且平面
 平面
平面 ,
,
∴ 平面
平面 .
.
∴ 为
为 在平面
在平面 内的射影.
内的射影.
 . --------10分
. --------10分
在 中,
中, ,
,
在 中,
中, ,
, .
.
∴ =
= .
------------11分
.
------------11分
所以直线 与平面
与平面 所成角的大小为
所成角的大小为 .
----12分
.
----12分
解法二:解:(Ⅰ)由已知 ,
,
以 点为原点,建立如图所示的空间直角坐标系
点为原点,建立如图所示的空间直角坐标系 .
.
则  ,
, .
-------2分
.
-------2分
则 ,
, .
.

 .
.
 .
----------------4分
.
----------------4分
(Ⅱ) ,
, 平面
平面 .
.
 是平面
是平面 的法向量. -------5分
的法向量. -------5分
设侧面 的法向量为
的法向量为
 ,
,
 ,
, .
.
 ,
,

 .令
.令 则
则 .
.
则得平面 的一个法向量
的一个法向量
 .
---------6分
.
---------6分
 .
.
即二面角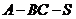 大小为60°. ----------8分
大小为60°. ----------8分
(Ⅲ)由(II)可知
 是平面
是平面 的一个法向量.
--------10分
的一个法向量.
--------10分
又 ,
,

 . -----11分
. -----11分
所以直线 与平面
与平面 所成角为
所成角为 ---------12分
---------12分
1.山东省莱芜市2008届高三年级期末考试
(本小题满分20分)如图,在三棱锥S-ABC中,SC⊥平面ABC,点P、M分别是SC和SB的中点,设PM=AC=1,∠ACB=90°,直线AM与直线SC所成的角为60°。
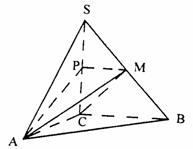 (1)求证:平面MAP⊥平面SAC。
(1)求证:平面MAP⊥平面SAC。
(2)(文)求二面角M-AC-B的平面角的正切值;
(理)求二面角M-AB-C的平面角的余弦值;
(3)(文)求多面体PMABC的体积。
(理)求AP和CM所成角的余弦值。
解:(I)∵SC⊥平面ABC,SC⊥BC,又∵∠ACB=90°
∴AC⊥BC,AC∩SC=C,BC⊥平面SAC,…………1分
又∵P,M是SC、SB的中点
∴PM∥BC,PM⊥面SAC,∴面MAP⊥面SAC,…………1分
(II)(文科)∵AC⊥平面SAC,∴面MAP⊥面SAC.…………3分
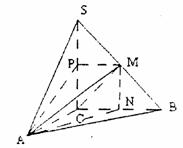 ∴AC⊥CM,AC⊥CB,从而∠MCB为二面角M-ACB的平面角,
∴AC⊥CM,AC⊥CB,从而∠MCB为二面角M-ACB的平面角,
∵直线AM与直线PC所成的角为60°
∴过点M作MN⊥CB于N点,连结AN,
则∠AMN=60°.……………………4分
在△CAN中,由勾股定理得
在Rt△AMN中,
= ………………6分
………………6分
在Rt△CNM中,
故二面角M-AB-C的正切值为 .…………………………8分
.…………………………8分
(理科)如图以C为原点建立如图所示空间直角坐标系C-xyz.
则
 ……………………4分
……………………4分
 设平面MAB的一个法向量为
设平面MAB的一个法向量为 ,则
,则
由
取z= ……………………6分
……………………6分
取平面ABC的一个法向量为
则
由图知二面角M-AB-C为锐二面角,
故二面角M-AB-C的余弦值为 ………………8分
………………8分
其他方法可参考本解法相应给分。
(3)(文科)多面体PMABC就是四棱锥A-BCPM
VPMABC=BA-PMBC=
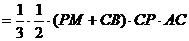
 ………………12分
………………12分
(理科) ………………9分
………………9分


∴AP与CM所成角的余弦值为 ………………12分
………………12分
5. 山东省潍坊市2008年5月高三教学质量检测(本小题满分12分)
山东省潍坊市2008年5月高三教学质量检测(本小题满分12分)
如图,三棱柱A1B1C1-ABC的三视图中,主视图和左视图是全等的矩形,俯视图是等腰直角三角形,已知点M是A1B1的中点.
(1)求证:B1C∥平面AC1M;
 (2)设AC与平面AC1M的夹角为θ,求sinθ.
(2)设AC与平面AC1M的夹角为θ,求sinθ.
解:由三视图可知三棱柱A1B1C1-ABC为直三棱柱,侧梭长为2,底面是等腰直角三角形,AC=BC=1.…………2分
 如图建立空间直角坐标系C-xyz,
如图建立空间直角坐标系C-xyz,
则C(0,0,0),C1(0,0,2),
A(1,0,0),B1(0,1,2),A1(1,0,2)
∵M为A1B1中点,
 …………………………4分
…………………………4分
(1)
 ……………………6分
……………………6分
 ∥面AC1M,又∵B1C
∥面AC1M,又∵B1C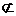 面AC1M,
面AC1M,
∴B1C∥面AC1M.…………………………8分
(2)设平面AC1M的一个法向量为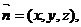

 …………………………………………………………10分
…………………………………………………………10分

则 …………………………12分
…………………………12分
4.山东省烟台市2008年高三适应性练习
(12分)如图,平面PAD⊥平面ABCD,ABCD为正方形,∠PAD=90°,且PA=AD=2,E、F、G分别是线段PA、PD、CD的中 点。
(1)求证:PB//平面EFG;
(2)求异面直线EG与BD所成的角的余弦值;
 (3)在线段CD上是否存在一点Q,使得点A到平面EFQ的距离为
(3)在线段CD上是否存在一点Q,使得点A到平面EFQ的距离为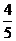 ,若存在,求出CQ的值;若不存在,请说明理由。
,若存在,求出CQ的值;若不存在,请说明理由。
解法一:(1)证明:取AB为中点H,连结GH,HE,
∵E,F,G分别是线段PA、PD、CD的中点,
∴GH//AD//EF,
∴E,F,G,H四点共面。……………………1分
又H为AB中点,
∴EH//PB。……………………2分
又EH 面EFG,PB
面EFG,PB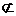 平面EFG,
平面EFG,
∴PB//面EFG。……………………4分
(2)解:取BC的中点M,连结GM、AM、EM,则GM//BD,
∴∠EGM(或其补角)就是异面直线EG与BD所成的角。……………………5分
在Rt△MAE中,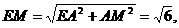
同理
∴在Rt△MGE中, ………………6分
………………6分
故异面直线EG与BD所成角的余弦值为 ……………………8分
……………………8分
(3)假设在线段CD上存在一点Q,满足题设条件,过点Q作OR⊥AB于R,连结RE,则QR//AD。
 ∵ABCD是正方形,△PAD是直角三角形
,且PA=AD=2,
∵ABCD是正方形,△PAD是直角三角形
,且PA=AD=2,
∴AD⊥AB,AD⊥PA
又AB PA=A,
PA=A,
∴AD⊥平面PAB。
又∵E,F分别是PA,PD中点,
∴EF//AD,
∴EF⊥平面PAB
又EF 面EFQ,
面EFQ,
∴EFQ⊥平面PAB。
过A作AT⊥ER于T,则AT⊥面EFQ,
∴AT就是点A到平面EFQ的距离。……………………10分
设
在Rt△EAR中,AT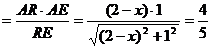
解得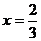 。
。
故存在点Q,当 时,点A到平面EFQ的距离为
时,点A到平面EFQ的距离为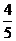 ………………12分
………………12分
解法二:建立如图所示的空间直角坐标系A-xyz,
则A(0,0,0),B(2,0,0,),C(2,2,0),
 D(0,2,0)P(0,0,2),E(0,0,1),
D(0,2,0)P(0,0,2),E(0,0,1),
F(0,1,1),G(1,2,0)。
(1)证明:∵
 ………………1分
………………1分
设
即(2,0,-2)=S(0,-1,0)+t(1,1,-1)
解得s=t=2
∴
又∵
∴ 共面。………………3分
共面。………………3分
∵
∴PB//平面EFG。……………………4分
(2)解∵ ……………………5分
……………………5分
∴
故平面直线EG与BD所成角的余弦值为 ………………8分
………………8分
(3)假设在线段CD上存在一点Q满足题设条件。
令 ,则DQ=2-m
,则DQ=2-m
∴点Q的坐标为( )
)
∴
而 ,则
,则

∴
令 ……………………10分
……………………10分
又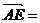 (0,0,1)
(0,0,1)
∴点A到平面EFQ的距离 …………11分
…………11分
即
∴ 不合题意,舍去。
不合题意,舍去。
故存在点Q,当 点A到平面EFQ的距离为
点A到平面EFQ的距离为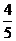 ………………12分
………………12分
考点五、利用向量求线面角
3.山东省郓城一中2007-2008学年第一学期高三期末考试
(理做Ⅰ、Ⅱ、Ⅲ;文做Ⅰ、Ⅳ)
如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F
 为CE上的点,且BF⊥平面ACE.
为CE上的点,且BF⊥平面ACE.
(Ⅰ)求证:AE⊥平面BCE;
(Ⅱ)求二面角B-AC-E的余弦值;
(Ⅲ)求点D到平面ACE的距离.
(Ⅳ)求证:平面BDF⊥平面ABCD
解法一:(Ⅰ) 平面ACE.
平面ACE. 
∵二面角D-AB-E为直二面角,且 ,
,
 平面ABE.
平面ABE.



(Ⅱ)连结BD交AC于C,连结FG,
∵正方形ABCD边长为2,∴BG⊥AC,BG= ,
,
 平面ACE,
平面ACE,
(Ⅲ)过点E作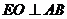 交AB于点O. OE=1.
交AB于点O. OE=1.
∵二面角D-AB-E为直二面角,∴EO⊥平面ABCD.
设D到平面ACE的距离为h,

 平面BCE,
平面BCE,

 ∴点D到平面ACE的距离为
∴点D到平面ACE的距离为
解法二:(Ⅰ)同解法一.
(Ⅱ)以线段AB的中点为原点O,OE所在直
线为x轴,AB所在直线为y轴,过O点平行
于AD的直线为z轴,建立空间直角坐标系
O-xyz,如图.
 面BCE,BE
面BCE,BE 面BCE,
面BCE,  ,
,
在 的中点,
的中点,

 设平面AEC的一个法向量为
设平面AEC的一个法向量为 ,
,
则 解得
解得
令 得
得 是平面AEC的一个法向量.
是平面AEC的一个法向量.
又平面BAC的一个法向量为 ,
,
 ∴二面角B-AC-E的大小为
∴二面角B-AC-E的大小为
(III)∵AD//z轴,AD=2,∴ ,
,
∴点D到平面ACE的距离
考点四、利用向量证明平行
2. 2008年金华一中高考模拟试卷(本小题满分14分)
如图,已知正三棱柱 ,
,
 是线段
是线段 上一点,且
上一点,且 ∥平面
∥平面 。记
。记 。
。
(1)求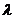 的值;
的值;
(2)若∠ ,求二面角
,求二面角 的大小;
的大小;

解:(1)连结 交
交 于O,则O是
于O,则O是 的中点,连结DO。
的中点,连结DO。
∵ ∥平面
∥平面 ,∴
,∴ ∥DO …………………………
∥DO …………………………
∴D为AC中点,∴ …………………
…………………
(2)设正三棱柱底面边长为2,则DC = 1。
∵∠ = 60°,∴
= 60°,∴ =
=  。
。
作DE⊥BC于E。∵平面 ⊥平面ABC,
⊥平面ABC,
 ∴DE⊥平面
∴DE⊥平面
 ,作EF⊥
,作EF⊥ 于F,连结DF,则 DF⊥
于F,连结DF,则 DF⊥
∴∠DFE是二面角D- -C的平面角……………………
-C的平面角……………………
在Rt△DEC中,DE= ,在Rt△BFE中,EF = BE·sin∠
,在Rt△BFE中,EF = BE·sin∠
∴在Rt△DEF中,tan∠DFE = 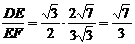
 ∴二面角D-
∴二面角D- -C的大小为arctan
-C的大小为arctan ………………
………………
解法二:以AC的中D为原点建立坐标系,如图,
设| AD | = 1,∵∠ =60°∴|
=60°∴| |
=
|
= 。
。
则A(1,0,0),B(0, ,0),C(-1,0,0),
,0),C(-1,0,0),
 (1,0
(1,0 ),
), ,
,
(2) =(-1,0,
=(-1,0, ),
),
设平面B D的法向量为
D的法向量为 ,则
,则 , 即
, 即
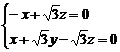 则有
则有 = 0令z = 1,则
= 0令z = 1,则 = (
= ( ,0,1)………………
,0,1)………………
设平面BC
 的法向量为
的法向量为 ,
,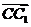 =(0,0,
=(0,0, ),
),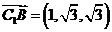
 即
即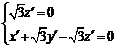 ∴z′= 0
∴z′= 0
令y = -1,解得 = (
= ( ,-1,0),
,-1,0), ,
,
二面角D-B -C的大小为arc cos
-C的大小为arc cos …………
…………
考点三、利用向量求距离
 考点一:利用向量证明垂直
考点一:利用向量证明垂直
1.山东省淄博市2008年5月高三模拟试题(本小题满分 分)
分)
已知梯形 中,
中, ∥
∥ ,
, ,
,  ,
, 、
、 分别是
分别是 、
、 上的点,
上的点, ∥
∥ ,
, ,
, 是
是 的中点.沿
的中点.沿 将梯形
将梯形 翻折,使平面
翻折,使平面 ⊥平面
⊥平面 (如图) .
(如图) .
 (Ⅰ) 当
(Ⅰ) 当 时,求证:
时,求证: ⊥
⊥ ;
;
(Ⅱ) 若以 、
、 、
、 、
、 为顶点的三棱锥的体积
为顶点的三棱锥的体积
记为  ,求
,求 的最大值;
的最大值;
(Ⅲ)当 取得最大值时,求二面角
取得最大值时,求二面角 的余弦值.
的余弦值.
 解:(Ⅰ)(法一)作
解:(Ⅰ)(法一)作 于
于 ,连
,连 ,
,
由平面 平面
平面 知
知  平面
平面
而 平面
平面 ,故
,故 又四边形
又四边形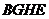
为正方形
∴ 
又 ,故
,故 平面
平面
而 平面
平面 ∴
∴  .
.
(或者直接利用三垂线定理得出结果)
 (法二)∵
平面
(法二)∵
平面 平面
平面
 ∴
∴  ⊥面平面
⊥面平面
∴  ⊥
⊥ ,
,  ⊥
⊥ ,又
,又 ⊥
⊥
故可如图建立空间坐标系 .则
.则
 ,
, ,
,
∴ 
∴  .
.
(Ⅱ) ∵  ,面
,面 面
面
∴  面
面
又由(Ⅰ) 平面
平面 ∴
∴ 
所以 
 =
=




即 时
时 有最大值为
有最大值为 .
.
(Ⅲ)(法一)作 于
于 ,作
,作 ,连
,连
由三垂线定理知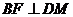
∴  是二面角
是二面角 的平面
的平面
角的补角
由 ∽
∽ ,知
,知

而 ,
,

∴  又
又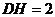
∴ 在 中,
中,
因为∠是 锐角 ∴
锐角 ∴ ∠
∠ =
=
而∠ 是二面角
是二面角 的平面角的补角
的平面角的补角
故二面角 的余弦值为-
的余弦值为- .
.
(法二)设平面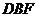 的法向量为
的法向量为
∵  ,
,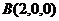 ,
, ,
,
∴ 

则 即
即
取  则
则  ∴
∴ 
面 的一个法向量为
的一个法向量为
则 <
< >
>
由于所求二面角 的平面角为钝角
的平面角为钝角
所以,此二面角的余弦值为- .
.
考点二、利用向量求二面角
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com