
2.(2008年广东卷,数学文科,1)第二十九届夏季奥林匹克运动会将于2008年8月8日在北京举行,若集合A={参加北京奥运会比赛的运动员},集合B={参加北京奥运会比赛的男运动员}。集合C={参加北京奥运会比赛的女运动员},则下列关系正确的是( )
A.A B
B.B
B
B.B C
C.A∩B=C D.B∪C=A
C
C.A∩B=C D.B∪C=A
[解析]本题考查对集合概念的理解,易知B∪C=A,
[答案]D.
1.(2008年山东卷,数学文科理科,1)满足M {a1,
a2, a3, a4},且M∩{a1 ,a2, a3}={ a1·a2}的集合M的个数是( )
{a1,
a2, a3, a4},且M∩{a1 ,a2, a3}={ a1·a2}的集合M的个数是( )
(A)1 (B)2 (C)3 (D)4
[解析]本小题主要考查集合子集的概念及交集运算。集合 中必含有
中必含有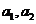 ,则
,则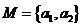 或
或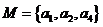
[答案]B
本节内容考试大纲的具体要求如下:
(1)集合的含义与表示
① 了解集合的含义、元素与集合的“属于”关系.
② 能用自然语言、图形语言、集合语言(列举法或描述法)描述不同的具体问题.
(2)集合间的基本关系
① 理解集合之间包含与相等的含义,能识别给定集合的子集.
② 在具体情境中,了解全集与空集的含义.
(3)集合的基本运算
① 理解两个集合的并集与交集的含义,会求两个简单集合的并集与交集.
② 理解在给定集合中一个子集的补集的含义,会求给定子集的补集.
③ 能使用韦恩(Venn)图表达集合的关系及运算.
(二)考点预测题
1(辽宁省部分重点中学协作体2008年高考模拟).在△ABC中,角A,B,C的对边为a,b,c,若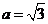 ,
,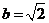 ,
,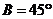 ,则角A=( )
,则角A=( )
A.30° B.30°或105° C.60° D.60°或120°
[解析]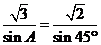 ,即
,即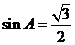 ,又
,又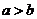 ,所以
,所以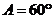 或
或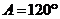 .
.
[答案]D.
2(2008年高考全国二17).在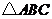 中,
中,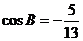 ,
,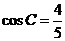 .
.
(Ⅰ)求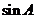 的值;
的值;
(Ⅱ)设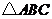 的面积
的面积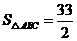 ,求
,求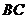 的长.
的长.
[解析](Ⅰ)由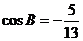 ,得
,得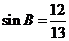 ,由
,由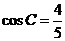 ,得
,得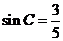 .
.
所以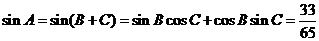 .
.
(Ⅱ)由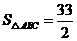 得
得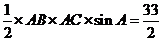 ,
,
由(Ⅰ)知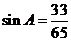 ,故
,故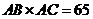 ,
,
又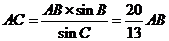 ,故
,故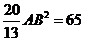 ,
,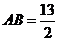 .
.
所以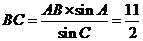 .
.
3(启东市2009届高三第一学期第一次调研考试 19)(2008年湖南理高考19).在一个特定时段内,以点E为中心的7海里以内海域被设为警戒水域.点E 正北55海里处有一个雷达观测站A.某时刻测得一艘匀速直线行驶的船只位于点A北偏东
19)(2008年湖南理高考19).在一个特定时段内,以点E为中心的7海里以内海域被设为警戒水域.点E 正北55海里处有一个雷达观测站A.某时刻测得一艘匀速直线行驶的船只位于点A北偏东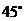 且与点A相距40
且与点A相距40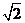 海里的位置B,经过40分钟又测得该船已行驶到点A北偏东
海里的位置B,经过40分钟又测得该船已行驶到点A北偏东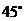 +
+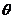 (其中sin
(其中sin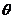 =
=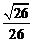 ,
,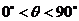 )且与点A相距10
)且与点A相距10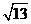 海里的位置C.
海里的位置C.
(1)求该船的行驶速度(单位:海里/小时);
(2)若该船不改变航行方向继续行驶.判断它是否会进入警戒水域,并说明理由.
[解析](1)如图,AB=40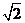 ,AC=10
,AC=10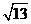 ,
,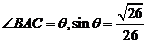 .
.
由于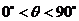 ,所以cos
,所以cos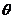 =
=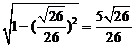 .
.
由余弦定理得BC=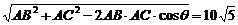
所以船的行驶速度为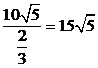 (海里/小时).
(海里/小时).
(2)解法一 如图所示,以A为原点建立平面直角坐标系,
设点B、C的坐标分别是B(x1,y2), C(x1,y2),BC与x轴的交点为D.
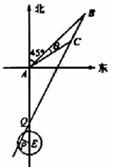 由题设有,x1=y1=
由题设有,x1=y1=
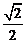 AB=40,
AB=40,
x2=ACcos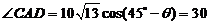 ,
,
y2=ACsin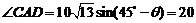 .
.
所以过点B、C的直线l的斜率k=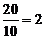 ,直线l的方程为y=2x-40.
,直线l的方程为y=2x-40.
又点E(0,-55)到直线l的距离d=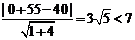 .
.
所以船会进入警戒水域.
解法二: 如图所示,设直线AE与BC的延长线相交于点Q.
在△ABC中,由余弦定理得:
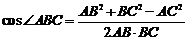 =
=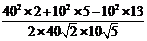 =
=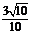 .
.
 从而
从而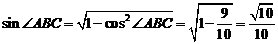 .
.
在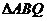 中,由正弦定理得,
中,由正弦定理得,
AQ=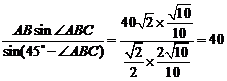 .
.
由于AE=55>40=AQ,所以点Q位于点A和点E之间,且QE=AE-AQ=15.
过点E作EP 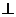 BC于点P,则EP为点E到直线BC的距离.
BC于点P,则EP为点E到直线BC的距离.
在Rt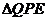 中,
中,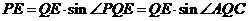
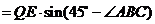 =
=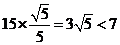 .
.
所以船会进入警戒水域.
(一)文字介绍
在解三角形中要求掌握正弦定理、余弦定理,并能解决一些简单的三角形度量问题,能够运用正弦定理、余弦定理等知识和方法解决一些与测量和几何计算有关的问题.在具体解三角形时,要灵活运用已知条件,根据正、余弦定理,列出方程,进而求解,最后还要检验是否符合题意.
解三角形是高考必考内容,重点为正、余弦定理及三角形面积公式.可以以小题形式主要考查考题正、余弦定理及三角形面积公式;也可以是简单的解答题,主要与三角函数的有关知识一起综合考查;随着课改的深入,联系实际,注重数学在实际问题中的应用将是一个热点,所以不排除考查解三角形与三角函数、函数等知识一起的综合应用题,主要
考查学生的基本运算能力、应用意识和解决实际问题的能力.
1(福建2008年高考样卷·文).△ABC的内角A、B、C所对的边分别为a、b、c,若sinA=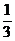 ,b=
,b=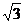 sinB,则a等于( )
A.
sinB,则a等于( )
A.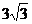 B.
B.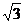 C.
C.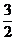 D.
D.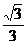
[解析]由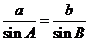 得
得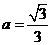 .
.
[答案]D.
2(山东省济南市2009届高三模考理10).在△ABC中,A=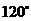 ,b=1,面积为
,b=1,面积为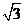 ,则
,则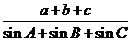 =( )
=( )
A.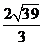 B.
B.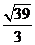 C.2
C.2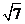 D.4
D.4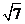
[解析]在△ABC中,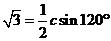 ,
,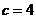 ;又
;又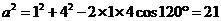 ,
,
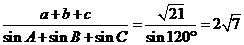 .
.
[答案]C.
3(2008-2009厦门质检二).在△ABC中,tanA=,cosB=.若最长边为1,则最短边的长为( )
A. B. C. D.
[解析]由条件知A、B都是小于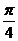 ,所以角C最大,又
,所以角C最大,又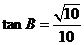 ,B最小,
,B最小,
由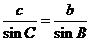 得,
得, ,所以最短边长为.
,所以最短边长为.
[答案]D.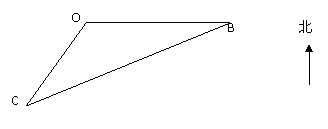
4(浙江省09年高考省教研室第一次抽样测试数学试题(理)16).如图,海平面上的甲船位于中心O的南偏西 ,与O相距10海里的C处,现甲船以30海里/小时的速度沿直线CB去营救位于中心O正东方向20海里的B处的乙船,甲船需要
小时到达B处.
,与O相距10海里的C处,现甲船以30海里/小时的速度沿直线CB去营救位于中心O正东方向20海里的B处的乙船,甲船需要
小时到达B处.
[解析]由题意,对于CB的长度可用余弦定理求解,得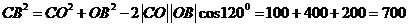 ,因此
,因此 ,因此甲船需要的时间为
,因此甲船需要的时间为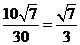 (小时).
(小时).
[答案] .
.
5 (江苏省南京市2009届高三第一次质量检测数学试题11) .在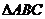 中,角
中,角 所对的边分别为
所对的边分别为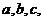
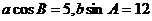 ,则
,则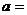 .
.
[解析]由 及正弦定理得:
及正弦定理得: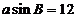 ,又
,又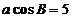 ,
,
两式平方相加得: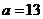 .
.
[答案]13.
6(浙江2008学年第一学期十校高三期末联考数学试题(理))
.在△ABC中,角A,B,C所对的边分别是a,b,c,若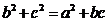 ,且
,且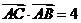 ,则△ABC的面积等于
.
,则△ABC的面积等于
.
[解析]由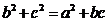 及余弦定理得:
及余弦定理得: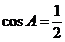 ,由
,由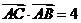 得
得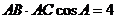 ,所以
,所以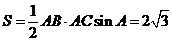 .
.
[答案]2 .
7(和平区2008年高考数学(理)三模13). 在△ABC中,设角A、B、C的对边分别为 ,且
,且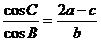 ,则角B= 度.
,则角B= 度.
[解析]由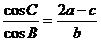 及正弦定理得:
及正弦定理得: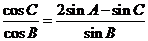 ,
,
 ,所以
,所以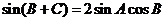 ,所以
,所以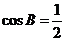 ,又
,又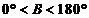 ,
,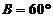 .
.
[答案]60.
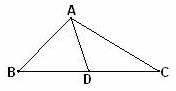 8(广东省四校联考2009届高三上学期期末考试数学理15).如图在
8(广东省四校联考2009届高三上学期期末考试数学理15).如图在 中,
中,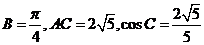
(1)求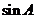 ; (2) 记
; (2) 记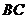 的中点为
的中点为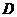 , 求中线
, 求中线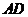 的长.
的长.
 [解析](1)由
[解析](1)由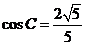 ,
, 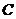 是三角形内角,
是三角形内角,
得
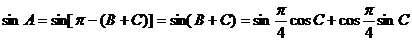
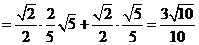
(2) 在△ABC中,由正弦定理,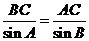 ,
,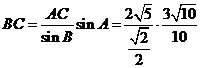
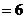
Þ CD = BC = 3 , 又在△ADC中, AC=2, cosC = ,
由余弦定理得, 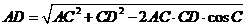
=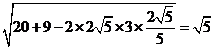
9(2009年滨海新区五所重点学校联考理17).在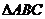 中,
中, 分别是角
分别是角 的对边,
的对边,
且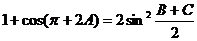 .
.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)当a=6时,求其面积的最大值,并判断此时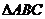 的形状.
的形状.
[解析](Ⅰ)由已知得: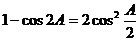 ,
,
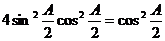 ,
,
 ,∴
,∴ 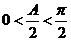
 ,
,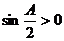
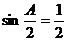 ,∴
,∴ 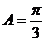 .
.
(Ⅱ) 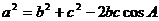 ,∴
,∴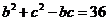 ,
,
∴
 .
.
故三角形的面积 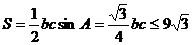 .
.
当且仅当b=c时等号成立;又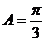 ,故此时
,故此时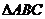 为等边三角形.
为等边三角形.
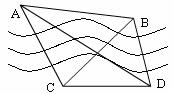 10(汉沽一中2009届高三月考文18).如图,隔河看两目标A、B,但不能到达,在岸边选取相距
10(汉沽一中2009届高三月考文18).如图,隔河看两目标A、B,但不能到达,在岸边选取相距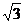 km的C、D两点,并测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°(A、B、C、D在同一平面内),求两目标A、B之间的距离.
km的C、D两点,并测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°(A、B、C、D在同一平面内),求两目标A、B之间的距离.
[解析]在△ACD中,∠ADC=30°,∠ACD=120°,∴∠CAD=30°,
∴AC=CD=3.
在△BDC中,∠CBD=180°-(45°+75°)=60°,
由正弦定理,得BC= =
=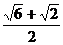 ,
,
由余弦定理,得AB2=AC2+BC2-2AC·BC·cos∠BCA
=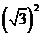 +
+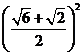 -2
-2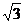 ×
×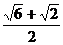 cos75°=5.∴AB=
cos75°=5.∴AB=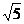 .
.
∴两目标A、B之间的距离为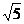 km.
km.
1(2008年高考山东卷15).已知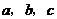 为
为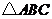 的三个内角
的三个内角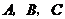 的对边,
的对边,
向量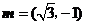 ,
,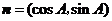 .若
.若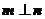 ,且
,且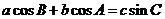 ,则角
,则角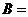 .
.
[解析]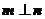
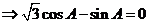
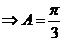 ,
,
由正弦定理得: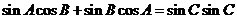 ,
,
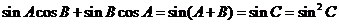
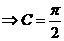
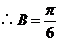 .
.
[答案]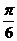 .
.
 2(2007年天津文17).在
2(2007年天津文17).在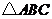 中,已知
中,已知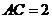 ,
,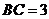 ,
,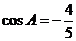 .
.
(Ⅰ)求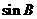 的值;
的值;
(Ⅱ)求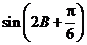 的值.
的值.
[解析](Ⅰ)在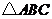 中,
中,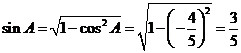 ,由正弦定理,
,由正弦定理,
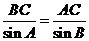 .
所以
.
所以 .
.
(Ⅱ)解:因为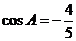 ,所以角
,所以角 为钝角,从而角
为钝角,从而角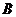 为锐角,于是
为锐角,于是
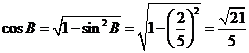 ,
,
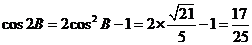 ,
,
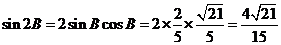 .
.
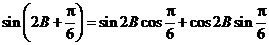
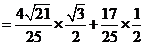
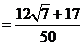 .
.
3(2008年高考重庆卷17).设 的内角A,B,C的对边分别为
的内角A,B,C的对边分别为 ,且
,且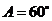 ,
,
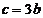 ,求:
,求:
(Ⅰ)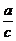 的值;
的值;
(Ⅱ)cotB +cot C的值.
[解析](Ⅰ)由余弦定理得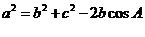 =
=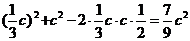
故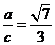 .
.
(Ⅱ)解法一: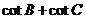 =
=
=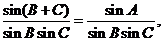
由正弦定理和(Ⅰ)的结论得
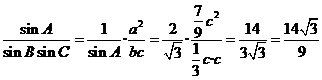 ,
,
故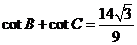 .
.
解法二:由余弦定理及(Ⅰ)的结论有
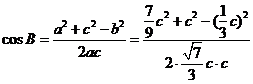 =
=
故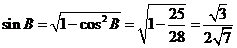 .
.
同理可得


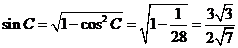 .
.
从而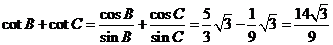 .
.
4(2008年高考辽宁卷17).在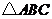 中,内角
中,内角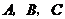 对边的边长分别是
对边的边长分别是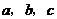 ,已知
,已知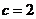 ,
,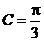 .
.
(Ⅰ)若 的面积等于
的面积等于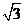 ,求
,求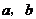 ;
;
(Ⅱ)若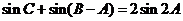 ,求
,求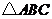 的面积.
的面积.
[解析](Ⅰ)由余弦定理及已知条件得,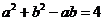 ,
,
又因为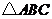 的面积等于
的面积等于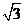 ,所以
,所以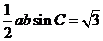 ,得
,得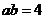 .
.
联立方程组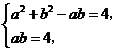 解得
解得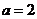 ,
,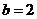 .
.
(Ⅱ)由题意得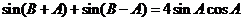 ,
,
即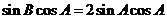 ,
,
当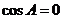 时,
时,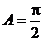 ,
,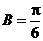 ,
,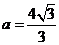 ,
,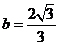 ,
,
当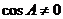 时,得
时,得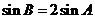 ,由正弦定理得
,由正弦定理得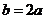 ,
,
联立方程组 解得
解得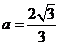 ,
,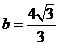 .
.
所以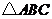 的面积
的面积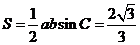 .
.
5(2008年高考全国一17).设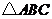 的内角
的内角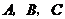 所对的边长分别为
所对的边长分别为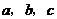 ,且
,且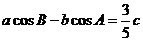 .
.
(Ⅰ)求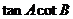 的值;
的值;
(Ⅱ)求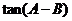 的最大值.
的最大值.
[解析](Ⅰ)在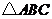 中,由正弦定理及
中,由正弦定理及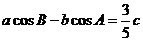
可得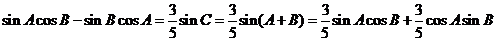
即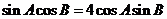 ,则
,则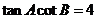 ;
;
(Ⅱ)由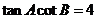 得
得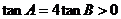
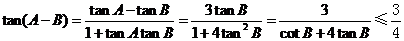
当且仅当 时,等号成立,
时,等号成立,
故当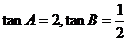 时,
时,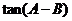 的最大值为
的最大值为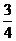 .
.
2.正弦定理和余弦定理的应用
能够运用正弦定理、余弦定理等知识和方法解决一些与测量和几何计算有关的实际问题.
解三角形是高考必考内容,重点为正余弦定理及三角形面积公式,考题灵活多样,近几年经常以解答题的形式来考查,若以解决实际问题为背景的试题,有一定的难度.
1.正弦定理和余弦定理
掌握正弦定理、余弦定理,并能解决一些简单的三角形度量问题.
2、 右图是《集合》的知识结构图,如果要加入“子集”,则应该放在( )
右图是《集合》的知识结构图,如果要加入“子集”,则应该放在( )
A.“集合的概念”的下位
B.“集合的表示”的下位
C.“基本关系”的下位
 D.“基本运算”的下位
D.“基本运算”的下位
答案:选C
说明:高考重点就是程序框图,考循环结构,在有限的时间内抓住要点。

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com