
2.(2007年上海卷,文科,21)
我们把由半椭圆
 与半椭圆
与半椭圆
 合成的曲线称作“果圆”,其中
合成的曲线称作“果圆”,其中 ,
, ,
, .
.
如图,设点 ,
, ,
, 是相应椭圆的焦点,
是相应椭圆的焦点, ,
, 和
和 ,
, 是“果圆” 与
是“果圆” 与 ,
, 轴的交点,
轴的交点,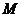 是线段
是线段 的中点.
的中点.
 (1)若
(1)若 是边长为1的等边三角形,求该
是边长为1的等边三角形,求该
“果圆”的方程;
(2)设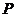 是“果圆”的半椭圆
是“果圆”的半椭圆
 上任意一点.求证:当
上任意一点.求证:当 取得最小值时,
取得最小值时,
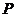 在点
在点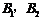 或
或 处;
处;
(3)若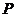 是“果圆”上任意一点,求
是“果圆”上任意一点,求 取得最小值时点
取得最小值时点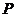 的横坐标.
的横坐标.
[解析](1)求出两个半椭圆的方程即可得到“果圆”的方程,(2)由两点间的距离公式表示出PM的长,根据二次函数的性质即可求出最小值,(3)思路同(2),只需分两种情况讨论即可.
[答案](1)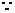
 ,
,
 ,
,
于是 ,
,
所求“果圆”方程为 ,
, .
.
(2)设 ,则
,则

 ,
,
 ,
,
 的最小值只能在
的最小值只能在 或
或 处取到.
处取到.
即当 取得最小值时,
取得最小值时,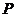 在点
在点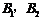 或
或 处.
处.
(3) ,且
,且 和
和 同时位于“果圆”的半椭圆
同时位于“果圆”的半椭圆 和半椭圆
和半椭圆 上,所以,由(2)知,只需研究
上,所以,由(2)知,只需研究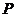 位于“果圆”的半椭圆
位于“果圆”的半椭圆 上的情形即可.
上的情形即可.

 .
.
当 ,即
,即 时,
时, 的最小值在
的最小值在 时取到,
时取到,
此时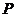 的横坐标是
的横坐标是 .
.
当 ,即
,即 时,由于
时,由于 在
在 时是递减的,
时是递减的, 的最小值在
的最小值在 时取到,此时
时取到,此时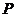 的横坐标是
的横坐标是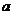 .
.
综上所述,若 ,当
,当 取得最小值时,点
取得最小值时,点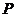 的横坐标是
的横坐标是 ;若
;若 ,当
,当 取得最小值时,点
取得最小值时,点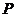 的横坐标是
的横坐标是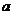 或
或 .
.
1. (2006年北京卷,文科,19)
椭圆C: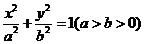 的两个焦点为F1,F2,点P在椭圆C上,且
的两个焦点为F1,F2,点P在椭圆C上,且
(Ⅰ)求椭圆C的方程;
(Ⅱ)若直线l过圆x2+y2+4x-2y=0的圆心M,交椭圆C于 两点,且A、B关于点M对称,求直线l的方程.
两点,且A、B关于点M对称,求直线l的方程.
[解析](Ⅰ)由椭圆的定义及勾股定理求出a,b,c的值即可,(Ⅱ)可以设出A、B点的坐标及直线方程,联立直线方程和椭圆方程后利用一元二次方程根与系数关系即可求出直线方程,也可以利用“点差法”求出直线的斜率,然后利用点斜式求出直线方程.
[答案]解法一:
(Ⅰ)因为点P在椭圆C上,所以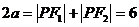 ,a=3.
,a=3.
在Rt△PF1F2中, 故椭圆的半焦距c=
故椭圆的半焦距c= ,
,
从而b2=a2-c2=4,
所以椭圆C的方程为 =1.
=1.
(Ⅱ)设A,B的坐标分别为(x1,y1)、(x2,y2).
已知圆的方程为(x+2)2+(y-1)2=5,所以圆心M的坐标为(-2,1).
从而可设直线l的方程为
y=k(x+2)+1,
代入椭圆C的方程得
(4+9k2)x2+(36k2+18k)x+36k2+36k-27=0.
因为A,B关于点M对称.
所以
解得 ,
,
所以直线l的方程为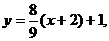
即8x-9y+25=0.
(经检验,所求直线方程符合题意)
解法二:
(Ⅰ)同解法一.
(Ⅱ)已知圆的方程为(x+2)2+(y-1)2=5,所以圆心M的坐标为(-2,1).
设A,B的坐标分别为(x1,y1),(x2,y2).由题意x1 x2且
x2且
 ①
①
 ②
②
由①-②得
 ③
③
因为A、B关于点M对称,
所以x1+ x2=-4, y1+ y2=2,
代入③得 =
=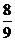 ,
,
即直线l的斜率为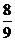 ,
,
所以直线l的方程为y-1=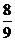 (x+2),
(x+2),
即8x-9y+25=0.
(经检验,所求直线方程符合题意.)
3.圆锥曲线中参数取值范围问题通常从两个途径思考:一是建立函数,用求值域的方法求范围,二是建立不等式,通过解不等式求范围.
2.当涉及到弦的中点时,通常有两种处理方法:一是韦达定理,二是点差法;
11. 圆锥曲线综合问题
⑴直线与圆锥曲线的位置关系和判定
直线与圆锥曲线的位置关系有三种情况:相交、相切、相离.
直线方程是二元一次方程,圆锥曲线方程是二元二次方程,由它们组成的方程组,经过消元得到一个一元二次方程,直线和圆锥曲线相交、相切、相离的充分必要条件分别是 、
、 、
、 .
.
⑵直线与圆锥曲线相交所得的弦长
直线具有斜率 ,直线与圆锥曲线的两个交点坐标分别为
,直线与圆锥曲线的两个交点坐标分别为 ,则它的弦长
,则它的弦长
上面的公式实质上是由两点间距离公式推导出来的,只是用了交点坐标设而不求的技巧而已(因为 ,运用韦达定理来进行计算.
,运用韦达定理来进行计算.
当直线斜率不存在是,则 .
.
注: 1.圆锥曲线,一要重视定义,这是学好圆锥曲线最重要的思想方法,二要数形结合,既熟练掌握方程组理论,又关注图形的几何性质,以简化运算;
10.方程的曲线和曲线的方程
在直角坐标系中,如果某曲线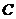 (看作点的集合或适合某种条件的点的轨迹)上的点与一个二元方程
(看作点的集合或适合某种条件的点的轨迹)上的点与一个二元方程 的实数解建立了如下的关系:
的实数解建立了如下的关系:
(1)曲线上的点的坐标都是这个方程的解;
(2)以这个方程的解为坐标的点都是曲线上的点,那么,这个方程叫做曲线的方程,这条曲线叫做方程的曲线.
9.抛物线知识网络

8.抛物线的标准方程及其几何性质:
|
标准方程 |
 |
 |
 |
 |
|
|
图形 |
 |
 |
 |
 |
|
|
对称轴 |
 轴 轴 |
 轴 轴 |
 轴 轴 |
 轴 轴 |
|
|
焦点 |
 |
 |
 |
 |
|
|
顶点 |
原点 |
||||
|
准线 |
 |
 |
 |
 |
|
|
离心率 |
 1 1 |
||||
7.抛物线的定义:
平面内到定点F和定直线l的距离相等的点的轨迹叫做抛物线(点F不在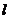 上).定点F叫做抛物线的焦点, 定直线
上).定点F叫做抛物线的焦点, 定直线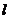 叫做抛物线的准线.
叫做抛物线的准线.
6.双曲线知识网络

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com