
5. (天津市十二区县重点中学)
(天津市十二区县重点中学)
(本小题满分14分)
已知函数
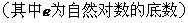
(Ⅰ)判断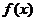 的奇偶性;
的奇偶性;
(Ⅱ)在 上求函数
上求函数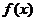 的极值;
的极值;
(Ⅲ)用数学归纳法证明:当 时,对任意正整数
时,对任意正整数 都有
都有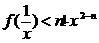
解:(Ⅰ) 
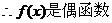 。……3分
。……3分
(Ⅱ)当 时,
时,
 ………5分
………5分
令 有
有 ,
,
当x变化时 的变化情况如下表: 由表可
的变化情况如下表: 由表可
知:
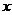 |
 |
 |
( |
 |
+ |
0 |
- |
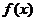 |
增 |
极大值 |
减 |
当 时
时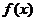 取极大值
取极大值 . ………7分
. ………7分
(Ⅲ)当 时
时 ………8分
………8分
考虑到: 时,不等式
时,不等式 等价于
等价于 …(1)
…(1)
所以只要用数学归纳法证明不等式(1)对一切 都成立即可………9分
都成立即可………9分
(i)当 时,设
时,设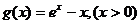
 , ………10分
, ………10分
故 ,即
,即
所以,当 时,不等式(1)都成立
………11分
时,不等式(1)都成立
………11分
(ii)假设 时,不等式(1)都成立,即
时,不等式(1)都成立,即
当 时设
时设
有 ………12分
………12分
故 为增函数,
为增函数,
所以, ,即
,即 , ………13分
, ………13分
这说明当 时不等式(1)也都成立,
时不等式(1)也都成立,
根据(i)(ii)可知不等式(1)对一切 都成立,
都成立,
故原不等式对一切 都成立.
………14分
都成立.
………14分
4. 已知函数
已知函数 ,数列
,数列 的前
的前 项和为
项和为 ,
, ,且
,且
 .
.
(Ⅰ)求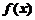 的最大值;
的最大值;
(Ⅱ)证明: ;
;
(Ⅲ)探究:数列 是否单调?
是否单调?
解:(Ⅰ)∵ ,∴
,∴ .
.
∵ =
= ,(2分)
,(2分)
∴当 时,
时, ,
, 在
在 上单调递增;
上单调递增;
当 时,
时, ,
, 在
在 上单调递减.
上单调递减.
∴在区间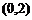 内,
内, .(2分)
.(2分)
(Ⅱ)用数学归纳法证明:
① 当 时,
∵
时,
∵ ,∴
,∴ ,
, 成立;
成立;
② 假设当 时,
时, 成立.
成立.
当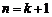 时,由
时,由 及
及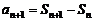 ,得
,得 ,(2分)
,(2分)
由(Ⅰ) 知, 在
在 上单调递增,所以
上单调递增,所以 ,
,
而 ,
, ,
故
,
故 .
.
∴当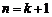 时,
时, 也成立.
也成立.
由①、②知, 对任意
对任意 都成立.(4分)
都成立.(4分)
(Ⅲ)数列 单调递减.(1分)
单调递减.(1分)
理由如下:
当 时,
时,
 ∴
∴ ;
;
当 时,由
时,由 得
得 .
.
∵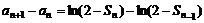
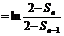 ,(2分)
,(2分)
又由 (Ⅱ) 知, ,∴
,∴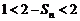 ,
,
∴ ,即
,即

∴ ,
,
∴ ,∴
,∴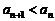 .(3分)
.(3分)
综上,数列 单调递减.
单调递减.
3.(浙江省重点中学2008年5月)
 已知函数
已知函数 ,数列
,数列 的前
的前 项和为
项和为 ,
, ,且
,且
 .
.
(Ⅰ)求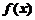 的最大值;
的最大值;
(Ⅱ)证明: ;
;
(Ⅲ)探究:数列 是否单调?
是否单调?
解:(Ⅰ)∵ ,∴
,∴ .
.
∵ =
= ,(2分)
,(2分)
∴当 时,
时, ,
, 在
在 上单调递增;
上单调递增;
当 时,
时, ,
, 在
在 上单调递减.
上单调递减.
∴在区间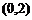 内,
内, .(2分)
.(2分)
(Ⅱ)用数学归纳法证明:
① 当 时,
∵
时,
∵ ,∴
,∴ ,
, 成立;
成立;
② 假设当 时,
时, 成立.
成立.
当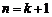 时,由
时,由 及
及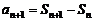 ,得
,得 ,(2分)
,(2分)
由(Ⅰ) 知, 在
在 上单调递增,所以
上单调递增,所以 ,
,
而 ,
, ,
故
,
故 .
.
∴当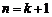 时,
时, 也成立.
也成立.
由①、②知, 对任意
对任意 都成立.(4分)
都成立.(4分)
(Ⅲ)数列 单调递减.(1分)
单调递减.(1分)
理由如下:
当 时,
时,
 ∴
∴ ;
;
当 时,由
时,由 得
得 .
.
∵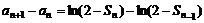
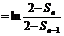 ,(2分)
,(2分)
又由 (Ⅱ) 知, ,∴
,∴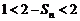 ,
,
∴ ,即
,即

∴ ,
,
∴ ,∴
,∴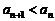 .(3分)
.(3分)
综上,数列 单调递减.
单调递减.
2.(湖南师大附中)(本小题满分14分)已知函数
(Ⅰ)试判断函数 上单调性并证明你的结论;
上单调性并证明你的结论;
(Ⅱ)若 恒成立,求整数k的最大值;
恒成立,求整数k的最大值;
(Ⅲ)求证:(1+1×2)(1+2×3)…[1+n(n+1)]>e2n-3.
.解:(I)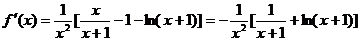 …………(2分)
…………(2分)

 上是减函数.……………………………………………………(4分)
上是减函数.……………………………………………………(4分)
(II)
即h(x)的最小值大于k.…………………………………………………………(6分)

则 上单调递增,
上单调递增,
又
 存在唯一实根a,且满足
存在唯一实根a,且满足
当
∴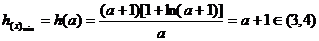
故正整数k的最大值是3 ……………………9分
(Ⅲ)由(Ⅱ)知
∴ ………………11分
………………11分
令 ,则
,则
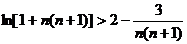
∴ln(1+1×2)+ln(1+2×3)+…+ln[1+n(n+1)]

∴(1+1×2)(1+2×3)…[1+n(n+1)]>e2n-3 ………………14分
1.(2008年潍坊市高三统一考试)
定义在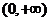 的三个函数f(x)、g(x)、h(x),已知f(x)=lnx,g(x)=
的三个函数f(x)、g(x)、h(x),已知f(x)=lnx,g(x)= 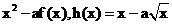 ,且g(x)在[1,2]为增函数,h(x)在(0,1)为减函数.
,且g(x)在[1,2]为增函数,h(x)在(0,1)为减函数.
(I)求g(x),h(x)的表达式;
(II)求证:当1<x<  时,恒有
时,恒有
(III)把h(x)对应的曲线 向上平移6个单位后得曲线
向上平移6个单位后得曲线 ,求
,求 与g(x)对应曲线
与g(x)对应曲线 的交点个数,并说明道理.
的交点个数,并说明道理.
解(I)由题意:

∴ 恒成立.
恒成立.

又 恒成立.
恒成立.
∴ 即
即
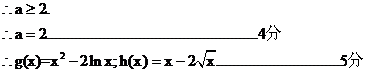
(II)
欲证:
只需证: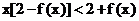
即证:
记
∴
∴当x>1时, 为增函数…………….9分
为增函数…………….9分

即
∴结论成立………………………………………………..10分
(III)由 (1)知:
∴ 对应表达式为
对应表达式为
∴问题转化成求函数
即求方程:
即:
设

 ∴当
∴当 时,
时, 为减函数.
为减函数.
 当
当 时,
时, 为增函数.
为增函数.
而 的图象开口向下的抛物线
的图象开口向下的抛物线
∴ 与
与 的大致图象如图:
的大致图象如图:
∴ 与
与 的交点个数为2个.
的交点个数为2个.
即 与
与 的交点个数为2个.
的交点个数为2个.
7.(2008福建卷19)(本小题满分12分)
已知函数 .
.
(Ⅰ)设{an}是正数组成的数列,前n项和为Sn,其中a1=3.若点 (n∈N*)在函数y=f′(x)的图象上,求证:点(n,Sn)也在y=f′(x)的图象上;
(n∈N*)在函数y=f′(x)的图象上,求证:点(n,Sn)也在y=f′(x)的图象上;
(Ⅱ)求函数f(x)在区间(a-1,a)内的极值.
本小题主要考查函数极值、等差数列等基本知识,考查分类与整合、转化与化归等数学思想方法,考查分析问题和解决问题的能力.满分12分.
(Ⅰ)证明:因为 所以
所以 ′(x)=x2+2x,
′(x)=x2+2x,
由点 在函数y=f′(x)的图象上,
在函数y=f′(x)的图象上,
又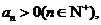 所以
所以
所以 ,又因为
,又因为 ′(n)=n2+2n,所以
′(n)=n2+2n,所以 ,
,
故点 也在函数y=f′(x)的图象上.
也在函数y=f′(x)的图象上.
(Ⅱ)解: ,
,
由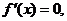 得
得 .
.
当x变化时,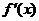 ﹑
﹑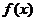 的变化情况如下表:
的变化情况如下表:
|
x |
(-∞,-2) |
-2 |
(-2,0) |
0 |
(0,+∞) |
|
f′(x) |
+ |
0 |
- |
0 |
+ |
|
f(x) |
↗ |
极大值 |
↘ |
极小值 |
↗ |
注意到 ,从而
,从而
①当 ,此时
,此时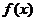 无极小值;
无极小值;
②当 的极小值为
的极小值为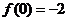 ,此时
,此时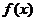 无极大值;
无极大值;
③当 既无极大值又无极小值.
既无极大值又无极小值.
6.(2008重庆卷20)(本小题满分13分.(Ⅰ)小问5分.(Ⅱ)小问8分.)
设函数 曲线y=f(x)通过点(0,2a+3),且在点(-1,f(-1))
曲线y=f(x)通过点(0,2a+3),且在点(-1,f(-1))
处的切线垂直于y轴.
(Ⅰ)用a分别表示b和c;
(Ⅱ)当bc取得最小值时,求函数g(x)=-f(x)e-x的单调区间.
解:(Ⅰ)因为
又因为曲线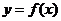 通过点(0,2a+3),
通过点(0,2a+3),
故
又曲线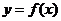 在(-1,f(-1))处的切线垂直于y轴,故
在(-1,f(-1))处的切线垂直于y轴,故
即-2a+b=0,因此b=2a.
(Ⅱ)由(Ⅰ)得
故当 时,
时, 取得最小值-
取得最小值- .
.
此时有
从而

所以
令 ,解得
,解得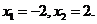
当
当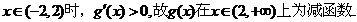
当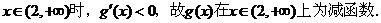
由此可见,函数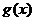 的单调递减区间为(-∞,-2)和(2,+∞);单调递增区间为(-2,2).
的单调递减区间为(-∞,-2)和(2,+∞);单调递增区间为(-2,2).
5..(2008陕西卷21).(本小题满分12分)
已知函数 (
( 且
且 ,
, )恰有一个极大值点和一个极小值点,其中一个是
)恰有一个极大值点和一个极小值点,其中一个是 .
.
(Ⅰ)求函数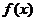 的另一个极值点;
的另一个极值点;
(Ⅱ)求函数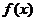 的极大值
的极大值 和极小值
和极小值 ,并求
,并求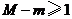 时
时 的取值范围.
的取值范围.
解:(Ⅰ) ,由题意知
,由题意知 ,
,
即得 ,(*)
,(*) ,
, .
.
由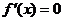 得
得 ,
,
由韦达定理知另一个极值点为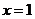 (或
(或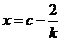 ).
).
(Ⅱ)由(*)式得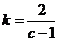 ,即
,即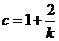 .
.
当 时,
时,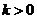 ;当
;当 时,
时, .
.
(i)当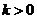 时,
时,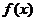 在
在 和
和 内是减函数,在
内是减函数,在 内是增函数.
内是增函数.
 ,
,
 ,
,
由 及
及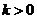 ,解得
,解得 .
.
(ii)当 时,
时,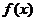 在
在 和
和 内是增函数,在
内是增函数,在 内是减函数.
内是减函数.
 ,
,
 恒成立.
恒成立.
综上可知,所求 的取值范围为
的取值范围为 .
.
4..(2008湖南卷21)(本小题满分13分)
已知函数f(x)=ln2(1+x)- .
.
(I) 求函数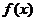 的单调区间;
的单调区间;
(Ⅱ)若不等式 对任意的
对任意的 都成立(其中e是自然对数的底数).
都成立(其中e是自然对数的底数).
求 的最大值.
的最大值.
解: (Ⅰ)函数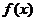 的定义域是
的定义域是 ,
,

设 则
则
令 则
则
当 时,
时,

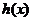 在(-1,0)上为增函数,
在(-1,0)上为增函数,
当x>0时,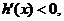
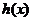 在
在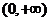 上为减函数.
上为减函数.
所以h(x)在x=0处取得极大值,而h(0)=0,所以 ,
,
函数g(x)在 上为减函数.
上为减函数.
于是当 时,
时,
当x>0时,
所以,当 时,
时,
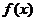 在(-1,0)上为增函数.
在(-1,0)上为增函数.
当x>0时,
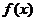 在
在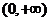 上为减函数.
上为减函数.
故函数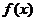 的单调递增区间为(-1,0),单调递减区间为
的单调递增区间为(-1,0),单调递减区间为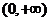 .
.
(Ⅱ)不等式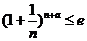 等价于不等式
等价于不等式 由
由 知,
知,
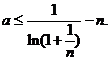 设
设 则
则

由(Ⅰ)知, 即
即
所以
 于是G(x)在
于是G(x)在 上为减函数.
上为减函数.
故函数G(x)在 上的最小值为
上的最小值为
所以a的最大值为
3.(2008山东卷21)(本小题满分12分)
已知函数 其中n∈N*,a为常数.
其中n∈N*,a为常数.
(Ⅰ)当n=2时,求函数f(x)的极值;
(Ⅱ)当a=1时,证明:对任意的正整数n,当x≥2时,有f(x)≤x-1.
(Ⅰ)解:由已知得函数f(x)的定义域为{x|x>1},
当n=2时,
所以 
(1)当a>0时,由f(x)=0得
 >1,
>1, <1,
<1,
此时 f′(x)= .
.
当x∈(1,x1)时,f′(x)<0,f(x)单调递减;
当x∈(x1+∞)时,f′(x)>0, f(x)单调递增.
(2)当a≤0时,f′(x)<0恒成立,所以f(x)无极值.
综上所述,n=2时,
当a>0时,f(x)在 处取得极小值,极小值为
处取得极小值,极小值为
当a≤0时,f(x)无极值.
(Ⅱ)证法一:因为a=1,所以
当n为偶数时,
令
则 g′(x)=1+ >0(x≥2).
>0(x≥2).
所以当x∈[2,+∞]时,g(x)单调递增,
又 g(2)=0
因此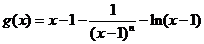 ≥g(2)=0恒成立,
≥g(2)=0恒成立,
所以f(x)≤x-1成立.
当n为奇数时,
要证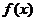 ≤x-1,由于
≤x-1,由于 <0,所以只需证ln(x-1) ≤x-1,
<0,所以只需证ln(x-1) ≤x-1,
令 h(x)=x-1-ln(x-1),
则 h′(x)=1- ≥0(x≥2),
≥0(x≥2),
所以 当x∈[2,+∞]时, 单调递增,又h(2)=1>0,
单调递增,又h(2)=1>0,
所以当x≥2时,恒有h(x) >0,即ln(x-1)<x-1命题成立.
综上所述,结论成立.
证法二:当a=1时,
当x≤2,时,对任意的正整数n,恒有 ≤1,
≤1,
故只需证明1+ln(x-1) ≤x-1.
令
则
当x≥2时, ≥0,故h(x)在
≥0,故h(x)在 上单调递增,
上单调递增,
因此 当x≥2时,h(x)≥h(2)=0,即1+ln(x-1) ≤x-1成立.
故 当x≥2时,有 ≤x-1.
≤x-1.
即f(x)≤x-1.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com