
1。命题预测
直线与圆是最基本的图形,是解析几何的基本内容,也是高考必考查的内容,试题多为选择和填空题,难度适中,属基本要求,但偶有与圆有关问题的解答题,其解答难度则可能较大。试题常在直线的图象、求直线方程,直线 的平行与垂直的位置关系,求圆面积的方程与有关圆的轨迹问题上作重点考查。同时有关对称问题也是高考的热点问题,其中直线与圆的位置关系与对称问题出现频率较高。而随着平面向量的出现,向量与直线或圆的综合问题则是一直高考的新热点。
圆锥曲线是平面解析几何的核心内容,因而是高考考查的重点内容。在每年的高考中一般有两道选择或填空题以及一道解答题。两道小题目通常是一道较易的“低档”题与一道“中档”题,主要考查圆锥曲线的标准方程及其几何性质等基础知识、基本技能以及基本方法的灵活运用,特别是要注意离心率的考察。而解答题则是注重对数学思想方法和数学语言的考查,重视对圆锥曲线定义的应用的考查。求轨迹以及直线与圆锥曲线的位置关系的考题,将注重考查与一元二次方程有关的判别式、韦达定理等腰三角形的应用。
4、(2008学年度第一学期上海市普陀区高三年级质量调研第16题)(本题满分12分)设点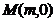 在椭圆
在椭圆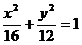 的长轴上,点
的长轴上,点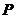 是椭圆上任意一点. 当
是椭圆上任意一点. 当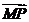 的模最小时,点
的模最小时,点 恰好落在椭圆的右顶点,求实数
恰好落在椭圆的右顶点,求实数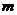 的取值范围.
的取值范围.
答案:解:设 为椭圆上的动点,由于椭圆方程为
为椭圆上的动点,由于椭圆方程为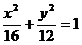 ,故
,故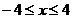 .
.
因为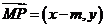 ,所以
,所以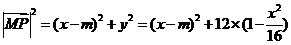
推出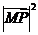
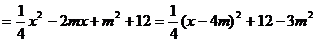 .
.
依题意可知,当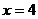 时,
时,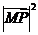 取得最小值.而
取得最小值.而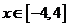 ,
,
故有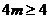 ,解得
,解得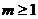 .
.
又点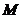 在椭圆的长轴上,即
在椭圆的长轴上,即 . 故实数
. 故实数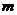 的取值范围是
的取值范围是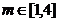 .
.
[点评]与圆锥曲线有关的最值问题、参数范围问题综合性较强,解题时需根据具体问题灵活的运用平面几何、函数、不等式等知识,正确的构造出圆锥曲线与其他数学知识的联系。
3、(金丽衢十二校高三第一次联考数学试卷(理科))
已知椭圆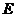 的中心在坐标原点,焦点在坐标轴上,且经过
的中心在坐标原点,焦点在坐标轴上,且经过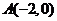 、
、 、
、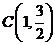 三点.
三点.
(1)求椭圆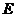 的方程:
的方程:
(2)若点D为椭圆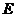 上不同于
上不同于 、
、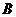 的任意一点,
的任意一点,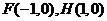 ,当
,当 内切圆的面积最大时。求内切圆圆心的坐标;
内切圆的面积最大时。求内切圆圆心的坐标;
(3)若直线 与椭圆
与椭圆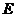 交于
交于 、
、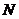 两点,证明直线
两点,证明直线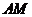 与直线
与直线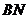 的交点在直线
的交点在直线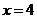 上.
上.
[解析](1)设椭圆方程为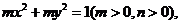
将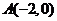 、
、 、
、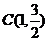 代入椭圆E的方程,得
代入椭圆E的方程,得
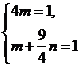 解得
解得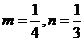 .
.
∴椭圆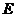 的方程
的方程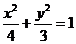 (4分)
(4分)
(2)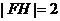 ,设
,设 边上的高为
边上的高为
当点 在椭圆的上顶点时,
在椭圆的上顶点时, 最大为
最大为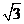 ,所以
,所以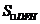 的最大值为
的最大值为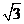 .
.
设 的内切圆的半径为
的内切圆的半径为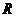 ,因为
,因为 的周长为定值6.所以
的周长为定值6.所以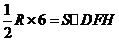 ,
,
所以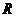 的最大值为
的最大值为 .所以内切圆圆心的坐标为
.所以内切圆圆心的坐标为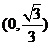 (10分)
(10分)
(3)法一:将直线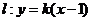 代入椭圆
代入椭圆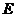 的方程
的方程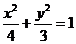 并整理.
并整理.
得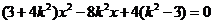 .
.
设直线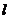 与椭圆
与椭圆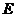 的交点
的交点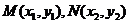 ,
,
由根系数的关系,得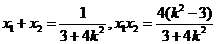 .
.
直线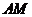 的方程为:
的方程为: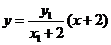 ,它与直线
,它与直线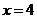 的交点坐标为
的交点坐标为
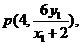 同理可求得直线
同理可求得直线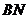 与直线
与直线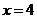 的交点坐标为
的交点坐标为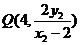 .
.
下面证明 、
、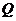 两点重合,即证明
两点重合,即证明 、
、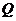 两点的纵坐标相等:
两点的纵坐标相等:
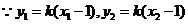 ,
,
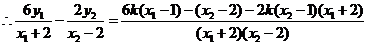

因此结论成立.
综上可知.直线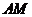 与直线
与直线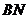 的交点住直线
的交点住直线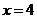 上. (16分)
上. (16分)
法二:直线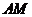 的方程为:
的方程为: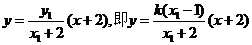
由直线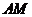 的方程为:
的方程为: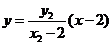 ,即
,即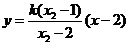
由直线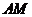 与直线
与直线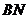 的方程消去
的方程消去 ,得
,得

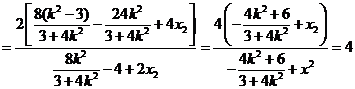
∴直线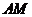 与直线
与直线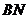 的交点在直线
的交点在直线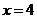 上.
上.
[点评]本题是将直线、圆与椭圆结合运用方程思想解题。
2、(辽宁省部分重点中学协作体2008年高考模拟)
在正△ABC中,D∈AB,E∈AC,向量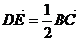 ,则以B,C为焦点,且过D,E的双曲线的离心率为 ( )
,则以B,C为焦点,且过D,E的双曲线的离心率为 ( )
A. B.
B.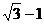 C.
C. D.
D.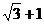
[解析]D.
[点评]由几何图形的性质得到关于a,b,c的齐次等式
1.(辽宁省沈阳二中2008-2009学年上学期高三期中考试)
直线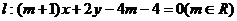 恒过定点C,圆C是以点C为圆心,以4为半径的圆。
恒过定点C,圆C是以点C为圆心,以4为半径的圆。
(1)求圆C的方程;
(2)设圆M的方程为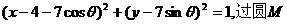 上任意一点P分别作圆C的两条切线PE、PF,切点为E、F,求
上任意一点P分别作圆C的两条切线PE、PF,切点为E、F,求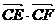 的最大值和最小值。
的最大值和最小值。
[解析](1) ,
,
(2)设 则
则

在 ,
,
由圆的几何性质得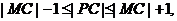
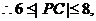
 ,由此可得
,由此可得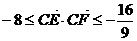
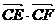 的最大值为-
的最大值为-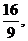 最小值为-8
最小值为-8
[点评]向量与解析几何结合是高考命题的重要趋势,本题难度不大。但是如果不能将“向量语言”准确转化为“函数语言”,或在解题中不细心都可能会出现错误。切记:“细节决定成败”
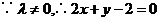
即点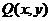 总在定直线
总在定直线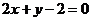 上
上
[点评]本题第一问是直接待定系数求出方程,第二问本质也是求动点轨迹是一条直线采用交轨法和参数法可求解。另外第二问还可以利用直线的参数方程解题。
4、(广东卷18).(本小题满分14分)
设 ,椭圆方程为
,椭圆方程为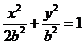 ,抛物线方程为
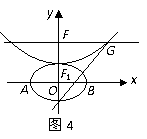
,抛物线方程为 .如图4所示,过点
.如图4所示,过点 作
作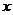 轴的平行线,与抛物线在第一象限的交点为
轴的平行线,与抛物线在第一象限的交点为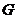 ,已知抛物线在点
,已知抛物线在点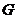 的切线经过椭圆的右焦点
的切线经过椭圆的右焦点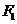 .
.
(1)求满足条件的椭圆方程和抛物线方程;
(2)设 分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点
分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点 ,使得
,使得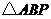 为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).
为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).
 [解析](1)由
[解析](1)由 得
得 ,
,
当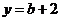 得
得 ,
,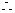 G点的坐标为
G点的坐标为 ,
,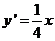 ,
,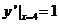 ,过点G的切线方程为
,过点G的切线方程为 即
即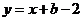 ,令
,令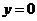 得
得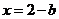 ,
,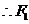 点的坐标为
点的坐标为 ,由椭圆方程得
,由椭圆方程得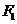 点的坐标为
点的坐标为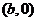 ,
,
 即
即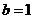 ,即椭圆和抛物线的方程分别为
,即椭圆和抛物线的方程分别为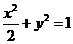 和
和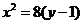 ;
;
(2)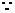 过
过 作
作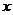 轴的垂线与抛物线只有一个交点
轴的垂线与抛物线只有一个交点 ,
,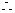 以
以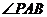 为直角的
为直角的 只有一个,
只有一个,
同理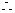 以
以 为直角的
为直角的 只有一个。
只有一个。
若以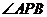 为直角,设
为直角,设 点坐标为
点坐标为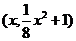 ,
, 、
、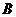 两点的坐标分别为
两点的坐标分别为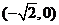 和
和 ,
,
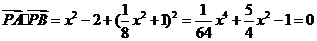 。
。
关于 的二次方程有一大于零的解,
的二次方程有一大于零的解,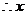 有两解,
有两解,
即以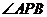 为直角的
为直角的 有两个,
有两个,
因此抛物线上存在四个点使得 为直角三角形。
为直角三角形。
(四) 圆锥曲线
1、(08福建卷11)又曲线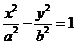 (a>0,b>0)的两个焦点为F1、F2,若P为其上一点,且|PF1|=2|PF2|,则双曲线离心率的取值范围为(B)
(a>0,b>0)的两个焦点为F1、F2,若P为其上一点,且|PF1|=2|PF2|,则双曲线离心率的取值范围为(B)
A.(1,3) B.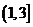 C.(3,+
C.(3,+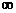 ) D.
) D.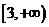
[解]PF1|-|PF2|=|PF2|=2a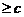 -a,故知e≤3又因为e>1,选B
-a,故知e≤3又因为e>1,选B
[点评]圆锥曲线的几何参量是高考重点,而几何参量中的离心率又是重中之重。
[突破]解决离心率的求值或求范围问题,重要是找到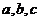 的齐次等式或不等式。
的齐次等式或不等式。
2、(08陕西卷8)双曲线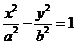 (
(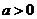 ,
, )的左、右焦点分别是
)的左、右焦点分别是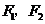 ,过
,过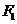 作倾斜角为
作倾斜角为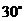 的直线交双曲线右支于
的直线交双曲线右支于 点,若
点,若 垂直于
垂直于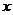 轴,则双曲线的离心率为( B )
轴,则双曲线的离心率为( B )
A. B.
B.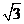 C.
C.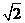 D.
D.
同上易知
3、(08安徽卷22).(本小题满分13分)
设椭圆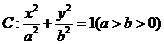 过点
过点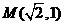 ,且着焦点为
,且着焦点为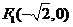
(Ⅰ)求椭圆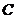 的方程;
的方程;
(Ⅱ)当过点 的动直线
的动直线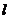 与椭圆
与椭圆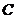 相交与两不同点
相交与两不同点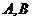 时,在线段
时,在线段 上取点
上取点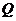 ,满足
,满足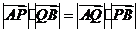 ,证明:点
,证明:点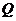 总在某定直线上
总在某定直线上
解 (1)由题意:
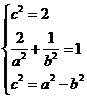 ,解得
,解得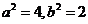 ,所求椭圆方程为
,所求椭圆方程为
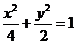
(2)方法一
设点Q、A、B的坐标分别为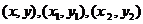 。
。
由题设知 均不为零,记
均不为零,记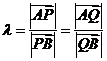 ,则
,则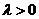 且
且
又A,P,B,Q四点共线,从而
于是
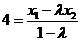 ,
,
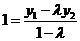
 ,
, 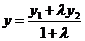
从而
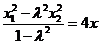 ,
, (1)
(1) 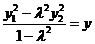 ,
, (2)
(2)
又点A、B在椭圆C上,即

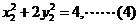
(1)+(2)×2并结合(3),(4)得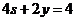
即点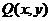 总在定直线
总在定直线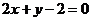 上
上
方法二
设点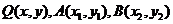 ,由题设,
,由题设, 均不为零。
均不为零。
且 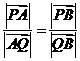
又 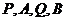 四点共线,可设
四点共线,可设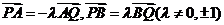 ,于是
,于是
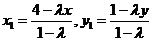 (1)
(1)
 (2)
(2)
由于 在椭圆C上,将(1),(2)分别代入C的方程
在椭圆C上,将(1),(2)分别代入C的方程
整理得
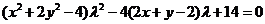 (3)
(3)
 (4)
(4)
(三) 直线与圆的位置关系
1、 (2008海南、宁夏文)已知m∈R,直线l: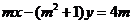 和圆C:
和圆C: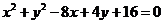 。
。
(1)求直线l斜率的取值范围;
(2)直线l能否将圆C分割成弧长的比值为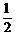 的两段圆弧?为什么?
的两段圆弧?为什么?
[解](Ⅰ)直线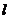 的方程可化为
的方程可化为 ,
,
直线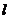 的斜率
的斜率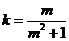 ,
,
因为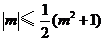 ,
,
所以 ,当且仅当
,当且仅当 时等号成立.
时等号成立.
所以,斜率 的取值范围是
的取值范围是 .
.
(Ⅱ)不能.
由(Ⅰ)知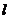 的方程为
的方程为
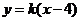 ,其中
,其中 .
.
圆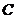 的圆心为
的圆心为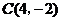 ,半径
,半径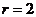 .
.
圆心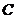 到直线
到直线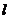 的距离
的距离
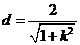 .
.
由 ,得
,得 ,即
,即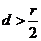 .从而,若
.从而,若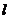 与圆
与圆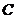 相交,则圆
相交,则圆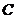 截直线
截直线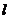 所得的弦所对的圆心角小于
所得的弦所对的圆心角小于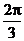 .
.
所以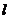 不能将圆
不能将圆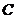 分割成弧长的比值为
分割成弧长的比值为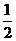 的两段弧.
的两段弧.
[点评]此题考查了直线方程,函数求值域,直线与圆的位置关系。难度不大但很好的综合了以上知识点。
[突破]注意把直线方程中的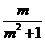 换成k使表达简单,减小运算量。
换成k使表达简单,减小运算量。
(二)圆
1、 (2008上海文、理)如图,在平面直角坐标系中,
(2008上海文、理)如图,在平面直角坐标系中,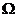 是一个与x轴的正半轴、y轴的正半轴分别相切于点C、D的定圆所围成的区域(含边界),A、B、C、D是该圆的四等分点.若点
是一个与x轴的正半轴、y轴的正半轴分别相切于点C、D的定圆所围成的区域(含边界),A、B、C、D是该圆的四等分点.若点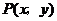 、点
、点 满足
满足 且
且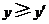 ,则称P优于
,则称P优于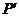 .如果
.如果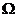 中的点
中的点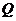 满足:
满足:
不存在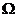 中的其它点优于Q,那么所有这样的点Q组成的集合是劣弧( D )
中的其它点优于Q,那么所有这样的点Q组成的集合是劣弧( D )
A. B. C. D.
[解]由题意可知Q点一定是圆上的一段弧且纵坐标较大横坐标较小,
故知是上半圆的左半弧。
[点评]此题是一个情景创设题,考查学生的应变能力。
[突破]Q点的纵坐标较大,横坐标较小。
2、(2008天津文)已知圆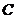 的圆心与点
的圆心与点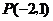 关于直线
关于直线 对称.直线
对称.直线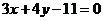 与圆
与圆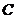 相交于
相交于 两点,且
两点,且 ,则圆
,则圆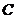 的方程为
的方程为 
[解]利用圆的标准方程待定系数易得结果。
[点评]此题虽小但考查到了对称、直线与圆相交、圆的方程等知识。
[突破]利用对称求出圆心坐标,利用直角三角形解出半径。
(一)直线
1、(2008四川文、理) 直线 绕原点逆时针旋转
绕原点逆时针旋转 ,再向右平移1个单位,所得到的直线为( A )
,再向右平移1个单位,所得到的直线为( A )
(A)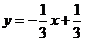 (B)
(B)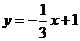 (C)
(C) (D)
(D)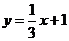
[解]∵直线 绕原点逆时针旋转
绕原点逆时针旋转 的直线为
的直线为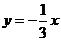 ,从而淘汰(C),(D)
,从而淘汰(C),(D)
又∵将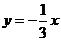 向右平移1个单位得
向右平移1个单位得 ,即
,即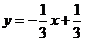 故选A;
故选A;
[点评]此题重点考察互相垂直的直线关系,以及直线平移问题;
[突破]熟悉互相垂直的直线斜率互为负倒数,过原点的直线无常数项;重视平移方法:“左加右减”;
2、 (2008江苏) 如图,在平面直角坐标系
(2008江苏) 如图,在平面直角坐标系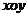 中,设三角形
中,设三角形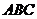 的顶点分别为
的顶点分别为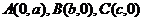 ,点
,点 在线段AO上的一点(异于端点),这里
在线段AO上的一点(异于端点),这里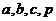 均为非零实数,设直线
均为非零实数,设直线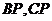 分别与边
分别与边 交于点
交于点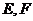 ,某同学已正确求得直线
,某同学已正确求得直线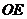 的方程为
的方程为 ,请你完成直线
,请你完成直线 的方程: (
的方程: ( 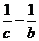 )
)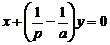 。
。
[解]画草图,由对称性可猜想填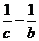 .事实上,由截距式可得直线AB:
.事实上,由截距式可得直线AB: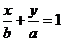 ,直线CP:
,直线CP: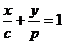 ,两式相减得
,两式相减得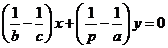 ,显然直线AB与CP 的交点F 满足此方程,又原点O 也满足此方程,故为所求直线OF 的方程.[答案]
,显然直线AB与CP 的交点F 满足此方程,又原点O 也满足此方程,故为所求直线OF 的方程.[答案]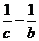
[点评]本小题考查直线方程的求法.
[突破]注意观察出对称性。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com