
5.下列命题错误的是( )
A.命题“若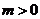 ,则方程
,则方程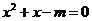 有实根”的逆否命题为:“若方程
有实根”的逆否命题为:“若方程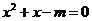 无实根,则
无实根,则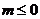 ”。
”。
B.“ ”是“
”是“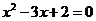 ”的充分不必要条件。
”的充分不必要条件。
C.命题“若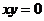 ,则
,则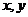 中至少有一个为零”的否定是:“若
中至少有一个为零”的否定是:“若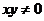 ,则
,则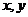 都不为零”。
都不为零”。
D.对于命题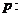
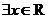 ,使得
,使得 ;则
;则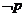 是
是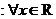 ,均有
,均有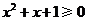 。
。
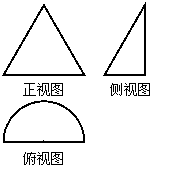
4.如图是某几何体的三视图,其中正视图是腰长为2的等腰三角形,
俯视图是半径为1的半圆,则该几何体的体积是( )
A.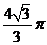 B.
B. C.
C.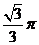 D.
D.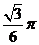
3.已知函数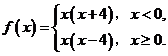 则函数
则函数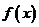 的零点个数为()
的零点个数为()
 A.1
B.2 C.3 D.4
A.1
B.2 C.3 D.4
2.如果复数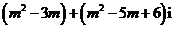 是纯虚数,则实数
是纯虚数,则实数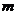 的值为()
的值为()
A.0 B.2 C.0或3 D.2或3
1.已知全集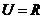 ,集合
,集合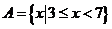 ,
,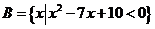 ,
,
则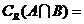 ( )
( )
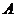 .
.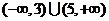
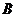 .
.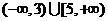
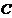 .
.
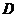 .
.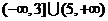
21.(本题满分14分)设函数f(x)=(1+x)2-ln(1+x)2.
(1)求f(x)的单调区间;
(2)若当 时,不等式f(x)<m恒成立,求实数m的取值范围;
时,不等式f(x)<m恒成立,求实数m的取值范围;
(3)若关于x的方程f(x)=x2+x+a在区间[0,2]上恰好有两个相异的实根,求实数a的取值范围.
本卷出题出发点:“发挥数学作为基础学科的作用,既重视考查中学数学基础知识的掌握程度,又注意考查进入高校继续学习的潜能”的要求,兼顾数学基础、方法、思维、应用和潜能等方面的考查,形成平稳发展的稳定格局。有利于高等学校选拔新生,有利于中学素质教育的实施,促进了数学教育改革的发展。突出对基础知识、基本技能、基本数学思想方法的考查。重视对数学基本能力和综合能力的考查。注重对数学应用意识和创新意识的考查。
本卷难度系数估计为:0.60--0.65

20. (本题满分14分)
设f1(x)=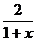 ,定义f n+1 (x) =f1 [f
n (x) ],
,定义f n+1 (x) =f1 [f
n (x) ],
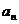 =
=  ,其中n
,其中n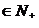
(1)
求数列{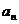 }的通项公式;
}的通项公式;
(2)若T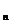 =1- (3n+1)
=1- (3n+1)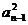 ,Qn=
,Qn=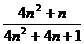 ,其中n
,其中n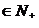 ,
,
试比较T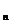 与Q
与Q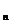 的大小。
的大小。
19.(本小题满分14分). 在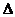 ABC中,
ABC中,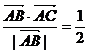 ,
, 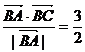 ,
,
又E点在BC边上,且满足3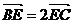 ,以A、B为焦点的双曲线经过C、E两点.
,以A、B为焦点的双曲线经过C、E两点.
(I)求此双曲线的方程;
(II)设P是此双曲线上任意一点,过A作∠APB平分线的垂线,垂足为M,求M点轨迹方程.
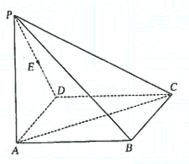
18.(本小题满分14分)如图,在四棱锥P-ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,AB=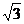 ,BC=1,PA=2,E为PD的中点.
,BC=1,PA=2,E为PD的中点.
(Ⅰ)求直线AC与PB所成角的余弦值;
(Ⅱ)在侧面PAB内找一点N,使NE⊥面PAC,并求出N点到AB和AP的距离.
17.(本小题满分12分)某华侨中学在状元林里一次性种植了n棵大树,各棵大树成活与否是相互独立的,在无人管理的情况下成活率为p,设ξ为无人管理情况下成活大树的棵数,其数学期望Eξ =14,其标准差为 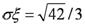 (Ⅰ)求n,p的值;
(Ⅱ)若有3棵或3棵以上的大树未成活,则需要补种,求不需要补种大树的概率。(运算结果可保留指数形式)
(Ⅰ)求n,p的值;
(Ⅱ)若有3棵或3棵以上的大树未成活,则需要补种,求不需要补种大树的概率。(运算结果可保留指数形式)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com