
16.从文中看,造成“动物全球化”的具体原因有哪些?(2分)
答:_______________________________________________________________________
动物也在全球化
张凯峰
①在全球化的浪潮中,人类社会正在变得越来越相似。人们使用同样的科技产品.追求同样的时尚,采取同样的生活方式,将来甚至还有可能使用同样的语言。“地球村”这个概念早已不是什么新鲜词了。人类变得彼此越来越相似。这事好还是不好.人们还在争论。
②在野生动物的世界里.同样的事情也正在生。所有地方的野生动物也正在长得越来
越像。科学家批评说,由于人类的流动,野生动植物也被迫加入了全球化的行列,从而使动植物品种的地区差异变得越来越淡。
③这种现象被称为“生物均质化”.这种观象对于生物世界的地区特性来说是一个重大的威胁。己经引起了自然资源保护管理论者的高度重视。事实上,人们不久前才刚刚开始认识到“生物均质化”意味着什么。所有生物在所有的地方生活,结果是地球上的生物种类会变得越来越少,同一物种之下的品种也会变得越来越单一。
④对物种地区差异威胁最明显的应该数物种入侵,物种利用人类的全球化贸易运输侵入
到其他地区,对当地的物种生存造成影响。比如说斑纹贻贝就通过船只播散到西欧和北美海
域。这些入侵物种会使当地的食物链陷入混乱.剥夺某些本地物种的生存空间。
⑤对生物多样性的更大成胁来自于人类对土地用途的改变。人类城市的扩张以及生物栖
息地的细碎化,使生物的生存环境越来越相似。这就会导致特定种类的生物过分繁盛。有些
适应能力极强的物种便如鱼得水,比如蟑螂、乌鸦、老鼠、浣熊、红狐和鹿。
⑥有些大脑容量相对较大的鸟类在人类对环境进行改造的时候应付自如,知道如何根据
环境的变化调整自己的生活方式,也能够很快接受前所未见的食物,而那些”小脑袋”鸟类就会受到相当太的打击,数量下降很快。于是在城市化的过程中,我们会越来越多地看到一些生物,而另一些则从我们的视野中消失了。
⑦由于人类一些不恰当的做法,野生动物种群的基目资源正在不断减少,将来一旦环境发
生重大改变,这将严重危及生态系统的适应力。
(选自《语文新圃》2009年第1期,略有改动)
15.文章第③段中加点的“这种现象”指代的具体内容是什么?(2分)
答:_______________________________________________________________________
18.从文中看,有效地解决水资源的季节分配和地区分布不均匀的办法分别是什么?(2分)
17.下面对文中划线句子的理解哪一项恰当?[ ](2分)
A.水、土资源的配合不合理,加剧了北方地区缺水状况。
B.水、土资源的配合不合理,会引起水、土资源的浪费。
C.水、土资源的配合不合理,导致了南北经济差异扩大。
D.水、土资源缺乏,致使小麦、棉花集中产区干旱严重。
我国水资源的季节分配和地区分布很不均匀,不仅制约了有限水资源的可利用性,也给开发利用带来诸多不便。夏季我国降水集中,汛期河水暴涨,大量宝贵的淡水资源白白流入大海,并且还容易造成洪涝灾害;冬春季则降水少,河流进入枯水期,北方的一些河流甚至干涸见底,造成严重的干旱缺水。我国水资源南丰北缺,南方水资源占全国的80%以上,北方仅占20%不到,特别是华北和西北地区,缺水最为严重。以我国小麦、棉花的集中产区华北平原为例,这里耕地面积约占全国的40%,但水资源仅占全国的6%左右。
兴建水利工程可以有效地解决水资源分布不均的问题。兴建水库,可以有效调控径流和水量的季节变化。例如,三峡工程和小浪底水利枢纽,建成后对长江和黄河的防洪及水资源调配发挥重要作用。跨流域调水,可以缓解一些地区严重缺水的状况。例如,引滦入津工程,将滦河水引入海河水系,缓解了天津市严重缺水的状况;引黄济青工程,将黄河水调入青岛,缓解了青岛市严重缺水的状况。
16.下面的说法哪一项不符合文意?[ ](2分)
A.夏季降水集中,汛期河水暴涨;冬春季则降水少,河流进入枯水期,这一现象表明我国水资源的季节分配不均匀。
B.水资源季节分配不均匀,既浪费了大量宝贵的淡水资源,使有限的水资源得不到有效利用,还容易造成洪涝灾害。
C.南方水资源占全国的80%以上,北方仅占20%不到,水资源南丰北缺这一事实说明,我国水资源的地区分布不均匀。
D.兴建水利工程可以有效提高水资源的可利用性,缓解北方地区的缺水状况,从根本上解决水资源缺乏的问题。
12. 已知1<m<n,m,n∈N*,求证:(1+m)n>(1+n)m.
证法一:由二项式定理(1+m)n=C m0+C
m0+C m1+…+C
m1+…+C mn,
mn,
(1+n)m=C n0+C
n0+C n1+…+C
n1+…+C ,
,
又因为C =
= ,C
,C =
= ,
,
而A mi>A
mi>A ,所以C
,所以C m2>C
m2>C ,C
,C >C
>C n3,…,C
n3,…,C >C
>C .
.
又因为C =C
=C ,C
,C =C
=C ,
,
所以(1+m)n>(1+n)m.
证法二:(1+m)n>(1+n)m nln(1+m)>mln(1+n)
nln(1+m)>mln(1+n)

 >
> . 令f(x)=
. 令f(x)= ,x∈[2,+∞],
,x∈[2,+∞],
只要证f(x)在[2,+∞]上单调递减,只要证f ′(x)<0.
f ′(x)= =
= .
.
当x≥2时,x-lg(1+x) <0,
<0,
x2(1+x)>0,得f ′(x)<0,即x∈[2,+∞]时,f ′(x)<0.
以上各步都可逆推,得(1+m)n>(1+n)m.
[探索题]已知数列 (n为正整数)是首项是a1,公比为q的等比数列.
(n为正整数)是首项是a1,公比为q的等比数列.
(1)求和:
(2)由(1)的结果归纳概括出关于正整数n的一个结论,并加以证明.
(3)设q≠1,Sn是等比数列 的前n项和,求:
的前n项和,求:
 .
.
解:(1)

(2)归纳概括的结论为:
若数列 是首项为a1,公比为q的等比数列,则
是首项为a1,公比为q的等比数列,则

(3)因为

11.求 展开式中系数最大的项
展开式中系数最大的项
解:设第 项系数最大,
项系数最大,
则有 ,即
,即



又
故系数最大项为
点评:二项式系数最大的项与系数最大的项不同 二项式系数最大的项也即中间项:当n为偶数时中间项
二项式系数最大的项也即中间项:当n为偶数时中间项 的二项式系数最大;当n为奇数时,中间两项
的二项式系数最大;当n为奇数时,中间两项 ,
, 的二项式系数相等且为最大
的二项式系数相等且为最大
10.如果在( +
+ )n的展开式中,前三项系数成等差数列,求展开式中的有理项.
)n的展开式中,前三项系数成等差数列,求展开式中的有理项.
解:展开式中前三项的系数分别为1, ,
, ,
,
由题意得2× =1+
=1+ ,得n=8.
,得n=8.
设第r+1项为有理项,T =C
=C ·
· ·x
·x ,则r是4的倍数,所以r=0,4,8.
,则r是4的倍数,所以r=0,4,8.
有理项为T1=x4,T5= x,T9=
x,T9= .
.
9.求式子(|x|+ -2)3的展开式中的常数项
-2)3的展开式中的常数项
解法一:(|x|+ -2)3=(|x|+
-2)3=(|x|+ -2)(|x|+
-2)(|x|+ -2)(|x|+
-2)(|x|+ -2)得到常数项的情况有:
-2)得到常数项的情况有:
①三个括号中全取-2,得(-2)3;
②一个括号取|x|,一个括号取 ,一个括号取-2,得C
,一个括号取-2,得C C
C (-2)=-12,
(-2)=-12,
∴常数项为(-2)3+(-12)=-20
解法二:(|x|+ -2)3=(
-2)3=( -
- )6,设第r+1项为常数项,
)6,设第r+1项为常数项,
则T =C
=C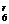 ·(-1)r·(
·(-1)r·( )r·|x|
)r·|x| =(-1)6·C
=(-1)6·C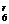 ·|x|
·|x| ,
,
得6-2r=0,r=3. ∴T3+1=(-1)3·C =-20
=-20
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com