46.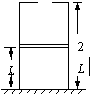(宝山区)如图所示，有一圆柱形汽缸，上部有一固定挡板，汽缸内壁的高度是2L，一个很薄且质量不计的活塞封闭一定质量的理想气体，开始时活塞处在离底部L高处，外界大气压为1.0×10⁵Pa，温度为27℃，现对气体加热，求：

(1)当加热到127℃时活塞离底部的高度；

(2)当加热到427℃时，气体的压强。

解析：开始加热活塞上升的过程封闭气体作等压变化。设气缸横截面积为S，活塞恰上升到气缸上部挡板处时气体温度为t℃，则对于封闭气体，状态一：T₁=(27+273)K，V₁=LS；状态二：T=(t+273)K，V=2LS。

由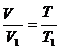，可得，解得t=327℃

(1)当加热到127℃时，活塞没有上升到气缸上部挡板处，设此时活塞离地高度为h，对于封闭气体，初状态：T₁=300K，V₁=LS末；末状态：T₂=400K，V₂=hS。

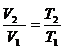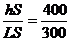由，可得 ，解得h=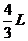

(2)设当加热到427⁰C时气体的压强变为p₃，在此之前活塞已上升到气缸上部挡板处，

对于封闭气体，初状态：T₁=300K，V₁=LS， p₁=1.0×10⁵Pa；

末状态：T₃=700K，V₃=2LS，p ₃=？

由，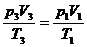

可得，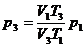

代入数据得：p₃=1.17×10⁵Pa

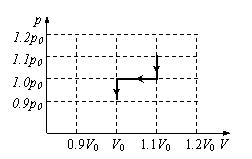
45.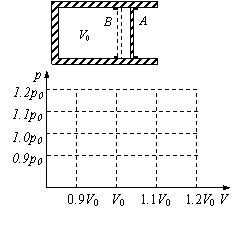(崇明县)如图所示，水平放置的汽缸内壁光

滑，活塞厚度不计，在A、B两处设有限制装

置，使活塞只能在A、B之间运动，B左面汽

缸的容积为V₀，A、B之间的容积为0.1V₀。开

始时活塞在A处，缸内气体的压强为1.1p₀

(p₀为大气压强且保持不变)，温度为399.3K，

现缓慢让汽缸内气体降温，直至297K。求：

(1)活塞刚离开A处时的温度T_A；

(2)缸内气体最后的压强p；

(3)在右图中画出整个过程的p-V图线。

解析：等容过程中活塞离开A时的温度为T_A

(1)

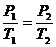
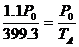
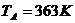
(2)等压过程中活塞到达B处时的温度为T_B

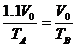
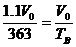
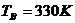
等容降温过程

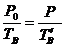
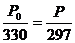
(也可以直接用状态方程做)

(3)图3分

44.(虹口区)一活塞将一定质量的理想气体封闭在气缸内，初始时气体体积为 3.0×l0 ^-3m³。用 DIS 实验系统测得此时气体的温度和压强分别为 300K 和1.0×10⁵Pa。推动活塞压缩气体，稳定后测得气体的温度和压强分别为320K和1.6×10⁵Pa。

　( 1)求此时气体的体积；

( 2)保持温度不变，缓慢改变作用在活塞上的力，使气体压强变为8.0×10⁴Pa，求此时气体的体积。

解析：(1)从气体状态Ⅰ到状态Ⅱ的变化符合理想气体状态方程

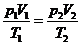
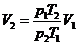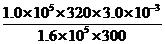　　　 =m³=2.0×10^-3 m³

　 (2)气体状态Ⅱ到状态Ⅲ的变化为等温过程

　　　 p₂V₂=p₃V₃　　　　　　　　　

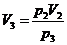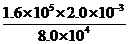　　　 = m³=4.0×10^-3 m³

44.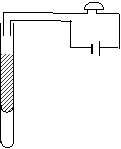(嘉定区)如图所示为一简易火灾报警装置。其原理是：竖直放置的试管中装有水银，当温度升高时，水银柱上升，使电路导通，蜂鸣器发出报警的响声。27℃时，空气柱长度L₁为20cm，水银上表面与导线下端的距离L₂为10cm，管内水银柱的高度h为8cm，大气压强为75cm水银柱高。

(1)当温度达到多少℃时，报警器会报警？

(2)如果要使该装置在87℃时报警，则应该再往玻璃管内注入多少cm高的水银柱？

(3)如果大气压增大，则该报警器的报警温度会受到怎样的影响？

解析：(1)等压变化＝　

＝

T₂＝450K　 t₂＝177℃

(2)设加入xcm水银柱，在87℃时会报警

＝

＝　

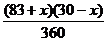
x＝8.14cm

(3)报警的温度会升高

43.(静安区)如图所示，一根粗细均匀、内壁光滑、竖直放置的玻璃管下端密封，上端留有一抽气孔．管内下部被活塞封住一定量的理想气体，气体温度为T₁．开始时，将活塞上方的气体缓慢抽出，当活塞上方的压强达到P₀时，活塞下方气体的体积为V₁，活塞上方玻璃管的容积为2.6V₁。活塞因重力而产生的压强为0.5P₀。继续将活塞上方抽成真空并密封，整个抽气过程中，管内气体温度始终保持不变，然后将密封的气体缓慢加热，求

　 (1)活塞刚碰到玻璃管顶部时气体的温度；

　 (2)当气体温度达到1.8T₁时气体的压强．

解析：(1)活塞上方压强为P₀时，活塞下方压强为P₀+0.5P₀。活塞刚到管顶时，下方气体压强为0.5P₀

设活塞刚到管顶时温度为T₂，由气态方程：

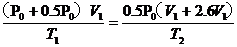
解得：T₂＝1.2 T₁

(2)活塞碰到顶部后，再升温的过程是等容过程。由查理定律得：

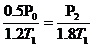
　 解得：P₂＝0.75P₀

1.0×10⁵×1.2×10^-3=4.17×10⁴×60×10^-4×h

　求得　　 h=0.48 m ＞容器高度　　

∴金属容器不能被提离地面　

1.0×10⁵×1.2×10^-3=1.17×10⁵×V₂

　　 求得 V₂=1.03×10^-3m³　　 h₂= V₂/S=1.03×10^-3/60×10^-4=0.17m

(2)活塞静止后关闭阀门, 假设当活塞被向上拉起至容器底部h高时,容器刚被提离地面,则气体的压强为P₃= P₀－Mg/S=1.0×10⁵－35×10/60×10^-4=4.17×10⁴ Pa

P₂V₂=P₃V₃　　

42.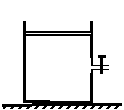(卢湾区)如图所示，放置在水平地面上一个高为40cm、质量为35kg的金属容器内密闭一些空气，容器侧壁正中央有一阀门，阀门细管直径不计．活塞质量为10kg，横截面积为60cm²．现打开阀门，让活塞下降直至静止．不计摩擦，不考虑气体温度的变化，大气压强为1.0×10⁵Pa ．活塞经过细管时加速度恰为g．求：

(1)活塞静止时距容器底部的高度；

(2)活塞静止后关闭阀门，对活塞施加竖直向上的拉力，是否能将金属容器缓缓提离地面？(通过计算说明)

解析：(1)活塞经阀门细管时, 容器内气体的压强为P₁=1.0×10⁵Pa，容器内气体的体积为V₁=60×10^-4×0.2m³=1.2×10^-3m³

活塞静止时,气体的压强为P₂=P₀+mg/S=1.0×10⁵+10×10/60×10^-4=1.17×10⁵ Pa

根据玻意耳定律，P₁V₁=P₂V₂

41.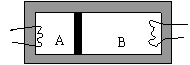(上海市南汇区)如图，水平放置的汽缸内壁光滑，一个不导热的活塞将汽缸内的气体分为A、B两部分，两部分气体可以分别通过放在其中的电热丝加热。开始时，A气体的体积是B的一半，A气体的温度是17ºC，B气体的温度是27ºC，活塞静止。现缓慢加热汽缸内气体， 使A、B两部分气体的温度都升高10ºC，在此过程中活塞向哪个方向移动？

某同学的解题思路是这样的：设温度升高后，左边气体体积增加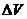，则右边气体体积减少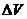，根据所给条件分别对两部分气体运用气态方程，讨论出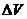的正负便可知道活塞移动方向。

你认为该同学的思路是否正确？如果认为正确，请按该同学思路确定活塞的移动方向；如果认为不正确，请指出错误之处，并通过计算确定活塞的移动方向。

解析：该同学思路正确。

对A有：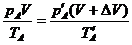

对B有：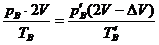

将已知条件代入上述方程，得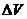＞0)

故活塞向右移动

还可以用下面方法求解：

设想先保持A、B的体积不变，当温度分别升高10ºC时，对A有

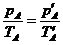
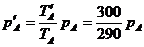
同理，对B有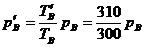

由于>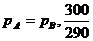

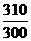
所以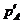>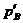，故活塞向右移动。