6.某工厂生产某种产品固定成本为2 000万元，并且每生产一单位产品，成本增加10万元.又知总收入K是单位产品数Q的函数，K(Q)＝40Q－Q²，则总利润L(Q)的最大值是　　　.

解析：总利润L(Q)＝40Q－Q²－10Q－2 000

＝－(Q－300)²+2 500.

故当Q＝300时，总利润最大值为2 500万元.

答案：2 500万元

5.某公司在甲、乙两地销售一种品牌车，利润(单位：万元)分别为L₁＝5.06x－0.15x²和L₂＝2x，其中x为销售量(单位：辆).若该公司在这两地共销售15辆车，则能获得最大利润为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A.45.606　 　　B.45.6 　　　C.45.56　 　　　　　D.45.51

解析：依题意可设甲销售x辆，则乙销售(15－x)辆，

∴总利润S＝5.06x－0.15x²+2(15－x)

＝－0.15x²+3.06x+30(x≥0).

∴当x＝10时，S_max＝45.6(万元).

答案：B

4.某工厂第三年的产量比第一年的产量增长44%，若每年的平均增长率相同(设为x)，则以下结论正确的是　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A.x＞22%

B.x＜22%

C.x＝22%

D.x的大小由第一年的产量确定

解析：(1+x)²＝1+44%，解得x＝0.2＜0.22.故选B.

答案：B

3.(2010·邯郸模拟)图形M(如图所示)是由底为1，高为1的等腰

三角形及高为2和3的两个矩形所构成，函数S＝S(a)(a≥0)是

图形M介于平行线y＝0及y＝a之间的那一部分面积，则函数

S(a)的图象大致是　　　　　　　　　　　　　　　　　 (　)

解析：依题意，当a≤1时，

S(a)＝+2a＝－+3a；

当1＜a≤2时，S(a)＝+2a；

当2＜a≤3时，S(a)＝+2+a＝a+；

当a＞3时，S(a)＝+2+3＝，

于是S(a)＝由解析式可知选C.

答案：C

2.某文具用品店出售羽毛球拍和羽毛球，球拍每副定价20元，羽毛球每只定价5元，该店制定了两种优惠方法：①买一副球拍赠送一只羽毛球；②按总价的92%付款.某人计划购买4副球拍，羽毛球30只，两种优惠方法中，更省钱的一种是　　　　 (　)

A.不能确定　 　　　　　　　　　　　B.①②同样省钱

C.②省钱　 　　　　　　　　　　　　D.①省钱

解析：①种方法需20×4+5×(30－4)＝210元，②种方法需(20×4+5×30)×92%＝211.6元.故①种方法省钱.

答案：D

1.已知A、B两地相距150千米，某人开汽车以60千米/小时的速度从A地到达B地，

B地 停留1小时后再以50千米/小时的速度返回A地，把汽车离开A地的距离x表示为时t(小时)的 函数表达式是　　　　　　　　　　　　　　　　　　　　　　 (　)

A.x＝60t+50t(0≤t≤6.5)

B.x＝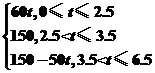

C.x＝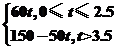

D.x＝

解析：依题意，函数为分段函数，求出每一段上的解析式即可.

答案：D

16、

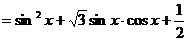
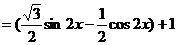
(1)

(2)当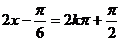即时；

(3)

13、 　　14、 　　　15、　 　

11、(1，3)或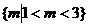　　 12 、　　 　5　

16、已知函数

　　 (1)求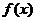的最小正周期；

　　 (2)求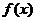的最大值及取得最大值时x的取值集合；

　　　 (3)若，求的值。

基础训练01

一　 选择题

二　 填空题