
3.互为反函数的两个函数具有相同的增减性
2.求一个函数的反函数图象的方法,
1.互为反函数的函数图象间关系,
补充:设函数y=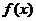 的反函数为y=
的反函数为y=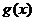 ,求y=
,求y=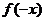 的反函数.
的反函数.
解:在函数y=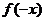 中,x为自变量,y为函数,且由题意知-x=
中,x为自变量,y为函数,且由题意知-x=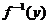 , ∴x=-
, ∴x=-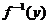 ,∴y=
,∴y=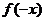 的反函数为y=-
的反函数为y=-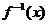 ,
,
又∵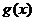 =
= 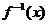 ,∴y=
,∴y=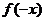 的反函数为y=-
的反函数为y=-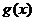 .
.
例1.求函数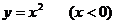 的反函数,并利用对称关系作出其反函数的图象.
的反函数,并利用对称关系作出其反函数的图象.
解:∵原函数的定义域是x<0,值域是y>0,
∴由y=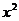 解出
解出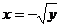 ,
,
∴函数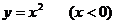 的反函数是
的反函数是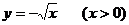 ,
,
作 y=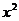 (x
(x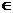 (-∞,0))的图象,再作该函数关于直线y=x的对称曲线,即为函数
(-∞,0))的图象,再作该函数关于直线y=x的对称曲线,即为函数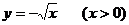 的图象(如图).
的图象(如图).
例2.求函数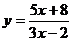 的值域.
的值域.
分析:灵活运用互为反函数的两个函数定义域和值域之间的关系.
解:∵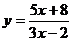 ∴
∴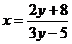 ∴ y≠
∴ y≠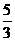
∴函数的值域为{y|y≠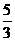 }
}
例3 已知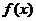 =
=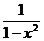 (x<-1),求
(x<-1),求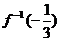 ;
;
解法1:⑴令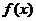 =y=
=y=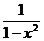 ,∴
,∴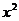 =
=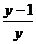 --①,∵x<-1,∴x=-
--①,∵x<-1,∴x=-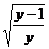 ;⑵∵x<-1,由①式知
;⑵∵x<-1,由①式知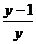 ≥1,∴y<0;
≥1,∴y<0;
⑶∴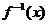 = -
= -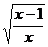 (x<0);⑷
(x<0);⑷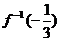 =-2.
=-2.
分析:由y=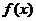 与y=
与y=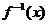 互为反函数的关系可知:当y=
互为反函数的关系可知:当y=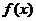 中的x=a时y=b,则在y=
中的x=a时y=b,则在y=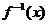 中,当x=b时y=a,本题要求
中,当x=b时y=a,本题要求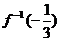 ,设其为u,说明在函数
,设其为u,说明在函数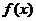 =y=
=y=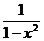 (x<-1)中,当y=
(x<-1)中,当y=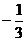 时,x=u,问题转化为知原来函数中的y=
时,x=u,问题转化为知原来函数中的y=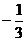 而求x.
而求x.
解法2:令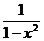 =
=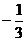 ,变形得
,变形得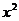 =1+3=4,又∵x<-1,∴x=-2.
=1+3=4,又∵x<-1,∴x=-2.
说明:解法2显然比解法1简捷得多,正确灵活地运用所学的有关概念,往往可以收到事半功倍的效果.
3.应用:⑴利用对称性作反函数的图像
若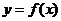 的图象已作出或比较好作,那么它的反函数
的图象已作出或比较好作,那么它的反函数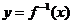 的图象可以由
的图象可以由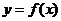 的图象关于直线y=x对称而得到;
的图象关于直线y=x对称而得到;
⑵求反函数的定义域求原函数的值域;
⑶反函数的单调性与原函数的单调性相同
2.证明结论(不要求掌握,根据实际情况处理)
 证明:设M(a,b)是
证明:设M(a,b)是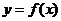 的图象上的任意一点,
的图象上的任意一点,
则当x=a时,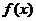 有唯一的值
有唯一的值 .
.
∵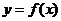 有反函数
有反函数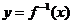 ,
,
∴当x=b时,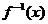 有唯一的值
有唯一的值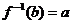 ,
,
即点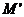 (b,a)在反函数
(b,a)在反函数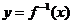 的图象上.
的图象上.
若a=b,则M,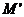 是直线y=x上的同一个点,它们关于直线y=x对称.
是直线y=x上的同一个点,它们关于直线y=x对称.
若a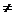 b,在直线y=x上任意取一点P(c,c),连结PM,P
b,在直线y=x上任意取一点P(c,c),连结PM,P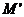 ,M
,M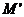
由两点间的距离公式得:
PM=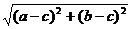 ,P
,P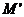 =
=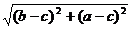 ,
,
∴PM=P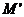 . ∴直线y=x是线段M
. ∴直线y=x是线段M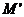 的垂直平分线,
的垂直平分线,
∴点M,
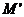 关于直线y=x对称.
关于直线y=x对称.
∵点M是y=f(x)的图象上的任意一点,
∴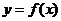 图象上任意一点关于直线y=x的对称点都在它的反函数
图象上任意一点关于直线y=x的对称点都在它的反函数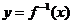 的图象上,由
的图象上,由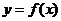 与
与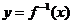 互为反函数可知,函数
互为反函数可知,函数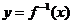 图象上任意一点关于直线y=x的对称点也都在它的反函数
图象上任意一点关于直线y=x的对称点也都在它的反函数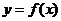 的图象上,
的图象上,
∴函数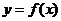 与
与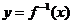 的图象关于直线y=x对称.
的图象关于直线y=x对称.
逆命题成立:若两个函数的图象关于直线y=x对称,则这两个函数一定是互为反函数.
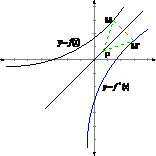
1.探究互为反函数的函数的图像关系
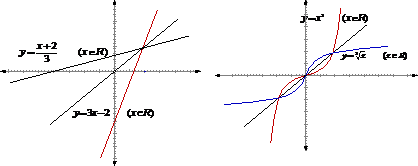
观察讨论函数、反函数的图像,归纳结论:函数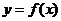 的图象和它的反函数
的图象和它的反函数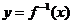 的图象关于直线
的图象关于直线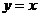 对称.
对称.
5.我们已经知道两个互为反函数的函数间有着必然的联系(在定义域、值域和对应法则方面). 函数图象是从“形”的方面反映这个函数的自变量x与因变量y之间的关系.因此,互为反函数的函数图象间也必然有一定的关系,今天通过观察如下图像研究-互为反函数的函数图象间的关系.
①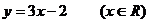 的反函数是
的反函数是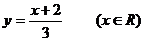

② 的反函数是
的反函数是

4. 在平面直角坐标系中,①点A(x,y)关于x轴的对称点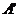 (x,-y);
(x,-y);
②点A(x,y)关于y轴的对称点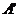 (-x,y);③点A(x,y)关于原点的对称点
(-x,y);③点A(x,y)关于原点的对称点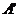 (-x,-y);④点A(x,y)关于y=x轴的对称点
(-x,-y);④点A(x,y)关于y=x轴的对称点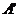 (?,?);
(?,?);
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com