
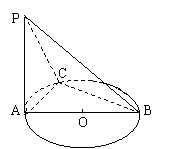
19、 如图,在底面是正方形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AD=a,E是PD的中点。
如图,在底面是正方形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AD=a,E是PD的中点。
(1)求证:PB∥平面AEC;
(2)求证:平面PDC⊥平面AEC;
(3)求点B到平面PDC的距离。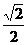 a
a
证明(1)连结BD交AC于0连结OE,可证得OE∥PB,故PB∥平面AEC
(2) PA⊥平面ABCD,
PA⊥平面ABCD, PA⊥CD,
PA⊥CD,
 底面是正方形,
底面是正方形,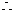 AD⊥CD
AD⊥CD
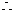 CD⊥平面PAD
CD⊥平面PAD
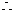 CD⊥AE
CD⊥AE
又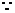 PA=AD,E是PD的中点,
PA=AD,E是PD的中点,
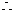 AE⊥PD
AE⊥PD
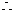 AE⊥平面PDC,故平面PDC⊥平面AEC
AE⊥平面PDC,故平面PDC⊥平面AEC
解(3)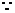 底面是正方形
底面是正方形
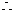 AB∥CD,
AB∥CD,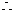 AB∥平面PDC
AB∥平面PDC
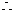 点B到平面PDC的距离即为点A到平面PDC的距离,
点B到平面PDC的距离即为点A到平面PDC的距离,
由(2)知AE⊥平面PDC
所以AE为点B到平面PDC的距离,
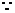 PA⊥平面ABCD,
PA⊥平面ABCD,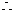 PA⊥AD,
PA⊥AD,
在RtΔPAD中,PA=AD,E是PD的中点,
所以AE=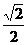 a,
a,
故点B到平面PDC的距离为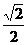 a。
a。
18、已知直线 :
: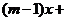
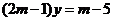 .
.
(1)若直线 的倾斜角为锐角,求m的取值范围;
的倾斜角为锐角,求m的取值范围;
(2)求证:不论m为何值时,直线 必过某一定点,并求出定点的坐标。(9,-4)
必过某一定点,并求出定点的坐标。(9,-4)
解:(1)因为直线 的倾斜角为锐角,
的倾斜角为锐角,
所以直线 的斜率k>0
的斜率k>0
又直线 的方程
的方程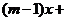
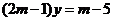 ,
,
所以k=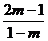 即
即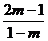 >0,解得
>0,解得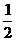 <m<1
<m<1
(2)直线 的方程
的方程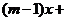
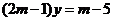 可化为
可化为
(x+2y-1)m-x-y+5=0
不论m为何值时,直线 过定点即为直线x+2y-1=0与直线-x-y+5=0的交点。
过定点即为直线x+2y-1=0与直线-x-y+5=0的交点。
解方程组可得定点为(9,-4)。
17、已知直线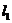 :
: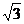 x-y+1=0,直线
x-y+1=0,直线 经过点A(1,2),求满足下列条件的直线
经过点A(1,2),求满足下列条件的直线 的方程。
的方程。
(1)直线 的倾斜角是直线
的倾斜角是直线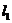 的倾斜角的2倍;
的倾斜角的2倍;
(2)直线 的倾斜角正弦值为
的倾斜角正弦值为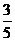 。3x-4y+5=0或3x+4y-11=0
。3x-4y+5=0或3x+4y-11=0
解(1)因为直线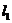 的方程为
的方程为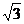 x-y+1=0,
x-y+1=0,
所以直线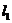 的斜率为
的斜率为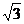 ,倾斜角的600
,倾斜角的600
故直线 的倾斜角为1200,斜率为-
的倾斜角为1200,斜率为-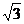
又直线 经过点A(1,2)
经过点A(1,2)
所以 方程为y-2=-
方程为y-2=-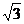 (x-1)即为
(x-1)即为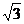 x+y-2-
x+y-2-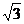 =0
=0
(2)设直线 的倾斜角为
的倾斜角为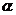 ,则sin
,则sin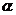 =
=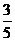
因为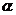 ∈
∈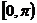 ,所以cos
,所以cos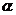 =±
=±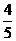 ,tan
,tan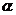 =±
=±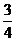
直线 经过点A(1,2)
经过点A(1,2)
故 方程为3x-4y+5=0或3x+4y-11=0。
方程为3x-4y+5=0或3x+4y-11=0。
16、已知PA⊥平面ABC, AB是⊙O的直径, C是⊙O上的任一点. 求证: BC⊥PC .
简证: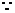 PA⊥平面ABC
PA⊥平面ABC
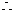 PA⊥BC
PA⊥BC
又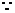 AB是⊙O的直径, C是⊙O上的任一点
AB是⊙O的直径, C是⊙O上的任一点
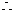 AC⊥BC
AC⊥BC
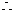 BC⊥平面PAC
BC⊥平面PAC
故BC⊥PC。
15、已知直线 经过点(2,-1),直线
经过点(2,-1),直线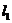 :3x-2y-1=0,求满足下列条件的直线
:3x-2y-1=0,求满足下列条件的直线 的方程
的方程
(1) ⊥
⊥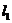 ;
;
(2) ∥
∥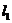 。解:(1)因为
。解:(1)因为 ⊥
⊥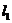 ,所以可设
,所以可设 的方程为2x+3y+c=0,
的方程为2x+3y+c=0,
又直线 经过点(2,-1)代入可解得c=-1,
经过点(2,-1)代入可解得c=-1,
故直线 的方程为2x+3y-1=0;
的方程为2x+3y-1=0;
(2)因为 ∥
∥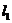 ,所以可设
,所以可设 的方程为3x-2y+m=0,
的方程为3x-2y+m=0,
又直线 经过点(2,-1)代入可解得m=-8,
经过点(2,-1)代入可解得m=-8,
故直线 的方程为3x-2y-8=0。
的方程为3x-2y-8=0。
14、已知A(-3,3),B(-1,-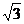 ),直线L过O(0,0)且与线段AB相交,则直线L的倾斜角的取值范围是________。
),直线L过O(0,0)且与线段AB相交,则直线L的倾斜角的取值范围是________。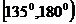 ∪
∪
13、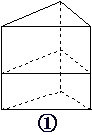 如图①所示一个正三棱柱形容器,高为2a,
如图①所示一个正三棱柱形容器,高为2a,
 内装水若干,将容器放倒使一个侧面成为底面,
内装水若干,将容器放倒使一个侧面成为底面,
这时水面恰为中截面,如图②,则未放倒前的
水面高度为_ __. 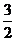 a
a
12、设 ,
,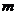 是两条不同的直线,
是两条不同的直线,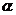 是一个平面,则下列命题正确的是___ ②________。
是一个平面,则下列命题正确的是___ ②________。
①若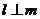 ,
,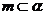 ,则
,则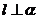 ②若
②若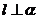 ,
,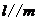 ,则
,则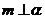
③若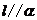 ,
,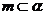 ,则
,则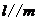 ④若
④若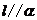 ,
,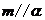 ,则
,则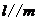
11、若直线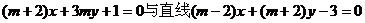 相互垂直,则m的值为
相互垂直,则m的值为 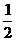 或-2 。
或-2 。
10、过点(2,1)且在两条坐标轴上截距相等的直线方程是__。x+y-3=0,x-2y=0
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com