3．直线与圆锥曲线相交的弦长公式

设直线l:y=kx+n，圆锥曲线：F(x,y)=0，它们的交点为P₁ (x₁,y₁)，P₂ (x₂,y₂)，

且由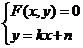，消去y→ax²+bx+c=0(a≠0)，Δ=b² －4ac。

则弦长公式为：

d====。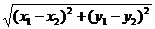

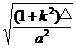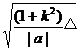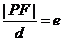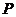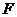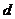焦点弦长：(点是圆锥曲线上的任意一点，是焦点，是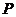到相应于焦点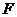的准线的距离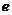，是离心率)。

2．直线与圆锥曲线的位置关系

直线与圆锥曲线的位置关系，从几何角度可分为三类：无公共点，仅有一个公共点及有两个相异公共点

直线与圆锥曲线的位置关系的研究方法可通过代数方法即解方程组的办法来研究。因为方程组解的个数与交点的个数是一样的

直线与圆锥曲线的位置关系可分为：相交、相切、相离．对于抛物线来说，平行于对称轴的直线与抛物线相交于一点，但并不是相切；对于双曲线来说，平行于渐近线的直线与双曲线只有一个交点，但并不相切．这三种位置关系的判定条件可引导学生归纳为：

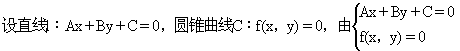_{[来源:Z§xx§]}

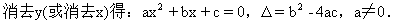
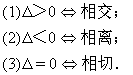
注意：直线与抛物线、双曲线有一个公共点是直线与抛物线、双曲线相切的必要条件，但不是充分条件．

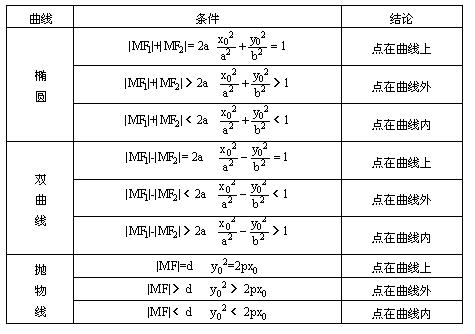
1．点M(x0，y0)与圆锥曲线C：f(x，y)=0的位置关系

2．与直线、圆锥曲线相结合的综合型考题，等轴双曲线基本不出题，坐标轴平移或平移化简方程一般不出解答题，大多是以选择题形式出现

近几年来直线与圆锥曲线的位置关系在高考中占据高考解答题压轴题的位置，且选择、填空也有涉及，有关直线与圆锥曲线的位置关系的题目可能会涉及线段中点、弦长等。分析这类问题，往往利用数形结合的思想和“设而不求”的方法，对称的方法及韦达定理等。

预测2011年高考：

1．会出现1道关于直线与圆锥曲线的位置关系的解答题；

2．掌握直线与圆锥曲线的位置关系判定及其相关问题

1．通过圆锥曲线与方程的学习，进一步体会数形结合的思想；

2．活动指导：写一首诗对于高中学生来说难度并不算很大，关键是如何提高诗歌的文学性和创新性。教师最好进行一定的指导，有兴趣的可以写一首下水诗歌。

1．提示：这几首诗由于作者不同，风格也表现出不同的特点，学生只要能言之有理的通过比较说出自己更喜欢某一首诗的理由就可以。