
8. 正方体的八个顶点中有四个恰为正四面体的顶点,则正方体的全面积与正四面体的全面积之比为( )
A.  B.
B. 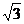 C.
C. 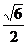 D.
D. 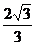
7. 如图所示,已知底面是正方形的四棱锥,其一条侧棱与底面垂直,它的长与底面边长相等,长度均为1,那么该棱锥中最长的棱长是( )
A.  B.
B. 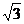 C.
C. 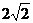 D. 3
D. 3
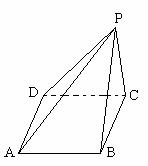
6. 已知三棱锥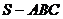 的三条侧棱两两互相垂直,SA=5,SB=4,SC=3,D为AB的中点,E为AC的中点,则四棱锥S-BCED的体积是( )
的三条侧棱两两互相垂直,SA=5,SB=4,SC=3,D为AB的中点,E为AC的中点,则四棱锥S-BCED的体积是( )
A. 10 B. 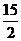 C.
C. 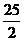 D.
D. 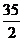
5. 棱锥被平行于底面的平面所截,当截面分别平分截锥的侧棱,侧面积、体积时,相应的截面面积分别为S1、S2、S3,则( )
A. 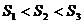 B.
B.
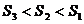
C. 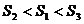 D.
D.

4. 设一个三棱锥的侧面与底面所成的角为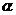 ,相邻两侧面所成的角为
,相邻两侧面所成的角为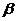 ,那么两个角
,那么两个角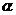 与
与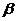 的三角函数关系是( )
的三角函数关系是( )
A. 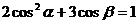 B.
B.
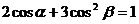
C. 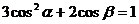 D.
D.
3. 侧面为等边三角形的正三棱锥,其侧面与底面所成二面角的余弦值为( )
A. 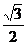 B.
B. 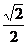 C.
C.  D.
D. 
2. 若正三棱锥的斜高是锥高的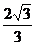 倍,则棱的侧面积是底面积的( )
倍,则棱的侧面积是底面积的( )
A. 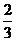 倍 B. 2倍 C.
倍 B. 2倍 C. 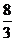 倍 D. 3倍
倍 D. 3倍
1. 正四棱锥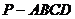 的侧面
的侧面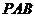 是等边三角形,E是PC的中点,则异面直线BE和PA所成的角的余弦值为( )
是等边三角形,E是PC的中点,则异面直线BE和PA所成的角的余弦值为( )
A. 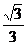 B.
B. 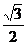 C.
C. 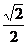 D.
D. 
3. 体积
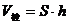
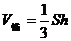
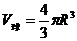
[典型例题]
[例1]
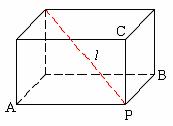
PA、PB、PC两两垂直,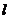 与PA、PB所成角为
与PA、PB所成角为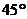 ,
,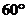 ,求
,求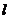 与PC所成角。
与PC所成角。
解:构造长方体
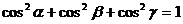

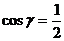
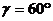
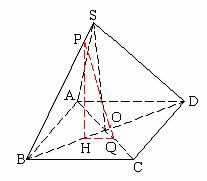
[例2]
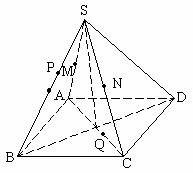
正四棱锥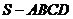 中,AB=
中,AB=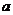 ,SA=
,SA=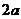 ,M为SA中点,N为SC中点。
,M为SA中点,N为SC中点。
(1)求BN、DM所成角
(2)P、Q在SB、CA上,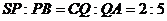 ,求PQ与底面ABCD所成角。
,求PQ与底面ABCD所成角。
解:
(1)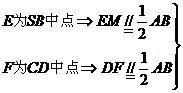
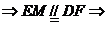

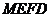
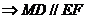
H为SN中点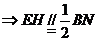
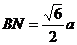

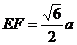
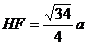
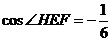
∴ 异面直线MD、BN所成角为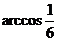
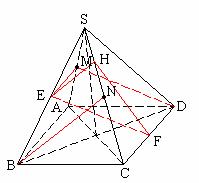
(2)过P作PH//SO交BD于H ∴ PH⊥面ABCD
∴ 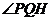 为PQ与底面所成角
为PQ与底面所成角
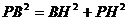 ∴
∴ 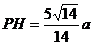
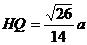
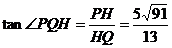 ∴
∴ 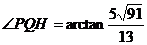
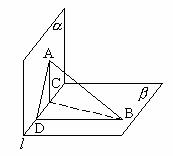
[例3] 直二面角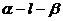 ,
,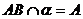 ,
,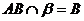 ,AB与
,AB与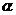 所成角为
所成角为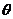 ,AB与
,AB与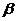 所成角为
所成角为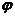 ,求证:
,求证: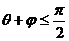 。
。
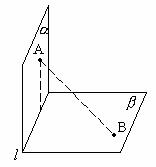
证明:过A作AC⊥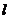 于C,过B作BD⊥
于C,过B作BD⊥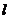 于D ∴
于D ∴ 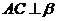
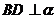

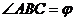 ∴
∴ 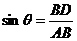
∴ 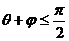
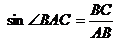
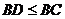 ∴
∴ 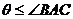
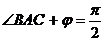
当且仅当C、D重合时,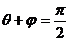
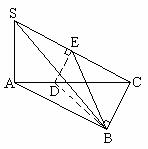
[例4] SA⊥面ABC,AB⊥BC,DE在面SAC内,垂直平分SC,交SC、AC于E、D,若SA=AB=1,BC= ,求二面角(1)
,求二面角(1)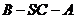 ;(2)
;(2)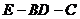 。
。
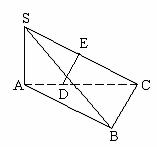
解:
(1)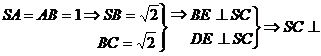 面DEB
面DEB
∴ 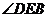 为二面角
为二面角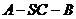 的平面角
的平面角
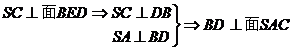
∴ 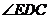 为二面角
为二面角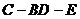 的平面角
的平面角
∴ 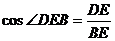
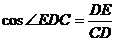
∵ AB=SA=1 AC=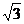 SC=2
SC=2
∴ BE=1 DE=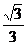 CD=
CD=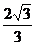 ∴
∴
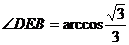
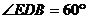
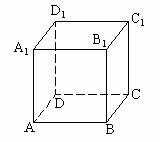
[例5] 正方体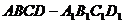 中,AB=1,求:
中,AB=1,求:
(1)D到面D1AC的距离
(2)C到面AB1D1的距离
(3)M为BB1中点,M到面D1AC的距离
(4)AC1与BB1的距离
解:
(1)连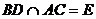
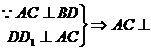 面
面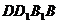
过D作DF⊥D1E于F,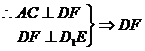 ⊥面D1AC
⊥面D1AC
∴ DF为距离 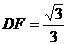

(2)设C到面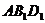 的距离为
的距离为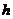
∴ 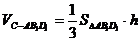
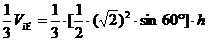
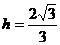
(3)连DM交D1E于H,设M到面D1AC距离为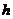
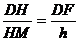
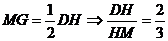 ∴
∴ 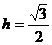
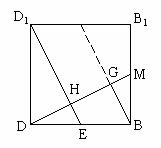
(4)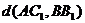
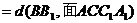
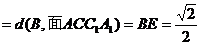
[例6] 四棱锥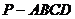 ,底面ABCD为菱形,AB=2,
,底面ABCD为菱形,AB=2,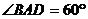 ,PB=PD,PA=PC=
,PB=PD,PA=PC=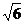 ,求:
,求:
(1)B到面PAD的距离
(2)BC与PA的距离
(3)AC与PD的距离
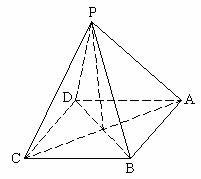
解:
(1)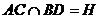 ,连PH
,连PH
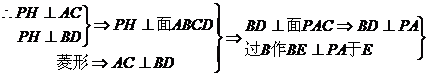
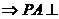 面DBE
面DBE
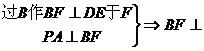 面PED
面PED
BF为所求 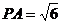
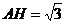
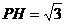 PB=2
PB=2
∴ BE=DE=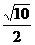 BD=2 ∴ BF=
BD=2 ∴ BF=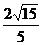
另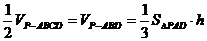
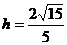

(2) (BC,面PAD)=
(BC,面PAD)=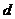 (B,面PAD)=
(B,面PAD)=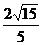
(3)过H作HM⊥PD于M
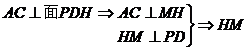 为公垂线
为公垂线
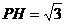 ,
,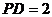 ,
,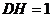
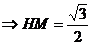
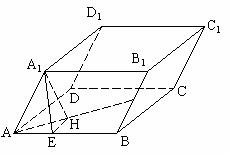
[例7] 斜四棱柱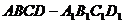 ,棱长均为2,
,棱长均为2,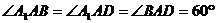 ,求四棱柱的体积。
,求四棱柱的体积。
解:过A1作A1H⊥面ABCD于H
∵ 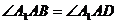
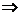 H在
H在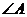 的平分线上
的平分线上
过H作HE⊥AB于E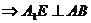
∴ 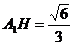
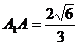
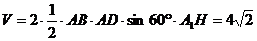
[模拟试题](答题时间:60分钟)
2. 距离
(1)作垂线
(2)体积转化
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com