4、注意理解波的图象及波的形成过程。

3、加深理解波是传递振动形式和波是能量传递的一种方式。

2、灵活应用简谐运动模型--单摆、弹簧振子。

1、从受力和运动两个方面分析简谐运动的特点及简谐运动中能量转化。

2． 人造地球卫星

⑴宇宙速度

第一宇宙速度

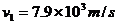，是地球卫星的最小发射速度，也是地球卫星在近地轨道上运行时的速度．

^由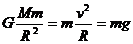得　．

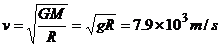例7、1990年3月，紫金山天文台将1965年9月20日发现的第2752号小行星命名为吴健雄星，其直径为32 km，如该小行星的密度和地球相同，则其第一宇宙速度为

　　　 m／s，已知地球半径R=6400km，地球的第一宇宙速度为8 km／s．(20m／s)

第二宇宙速度的计算

　　 如果人造卫星进入地面附近的轨道速度等于或大于1l.2km／s，就会脱离地球的引力，这个速度称为第二宇宙速度．

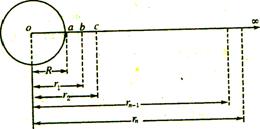　　 为了用初等数学方法计算第二宇宙速度，设想从地球表面至无穷远处的距离分成无数小段ab、bc、…，等分点对应的半径为r₁、r₂…，如下图所示．

由于每一小段ab、bc、cd…极小，这一小段上的引力可以认为不变．因此把卫星从地表a送到b时，外力克服引力做功

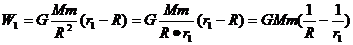
同理，卫星从地表移到无穷远过程中，各小段上外力做的功分别为

…

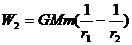
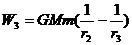
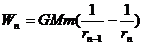
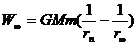
把卫星送至无穷远处所做的总功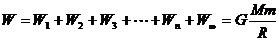　　

为了挣脱地球的引力卫星必须具有的动能为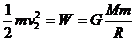

所以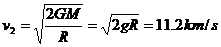

　 　第三宇宙速度的推算

脱离太阳引力的速度称为第三宇宙速度．因为地球绕太阳运行的速度为v_地＝30km/s，根据推导第二宇宙速度得到的脱离引力束缚的速度等于在引力作用下环绕速度的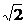倍，即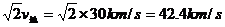

因为人造天体是在地球上，所以只要沿地球运动轨道的方向增加△v＝12.4km／s即可，即需增加动能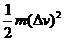．所以人造天体需具有的总能量为

得第三宇宙速度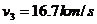

1． 万有引力定律提供天体做圆周运动的向心力

⑴人造地球卫星的绕行速度、角速度、周期与半径的关系

①由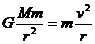得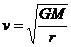　　　r越大，v越小

②由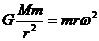得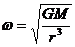　　　r越大，ω越小

③由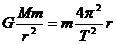得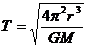　　r越大，T越大

例4、土星外层上有一个环。为了判断它是土星的一部分还是土星的卫星群，可以测量环中各层的线速度a与该l层到土星中心的距离R之间的关系来判断：　 ( AD )

A．若v∝R，则该层是土星的一部分；　　B．若v²∝R，则该层是土星的卫星群

C．若v∝1／R，则该层是土星的一部分 　 D．若v²∝1／R，则该层是土星的卫星群

⑵求天体质量、密度

由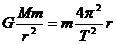　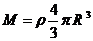 　即可求得

注意天体半径与卫星轨迹半径区别

⑶人造地球卫星的离心向心问题

例5、在地球大气层外有很多太空垃圾绕地球做匀速圆周运动，每到太阳活动期，由于受太阳的影响，地球大气层的厚度开始增加，从而使得部分垃圾进入大气层，开始做靠近地球的向心运动，产生这一结果的原因是　　 ( C　 )

A．由于太空垃圾受到地球引力减小而导致的向心运动

B．由于太空垃圾受到地球引力增大而导致的向心运动

C．由于太空垃圾受到空气阻力而导致的向心运动

D．地球引力提供了太空垃圾做圆周运动所需的向心力，故产生向心运动的结果与空气阻力无关

例6、宇宙飞船要与轨道空间站对接，飞船为了追上轨道空间站　　 ( A )

　 A．只能从较低轨道上加速

　 B．只能从较高轨道上加速

　 C．只能从同空间站同一高度轨道上加速

　 D．无论在什么轨道上，只要加速都行

5．物体在地面上所受的引力与重力的区别和联系

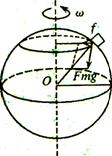地球对物体的引力是物体具有重力的根本原因．但重力又不完全等于引力．这是因为地球在不停地自转，地球上的一切物体都随着地球自转而绕地轴做匀速圆周运动，这就需要向心力．这个向心力的方向是垂直指向地轴的，它的大小是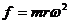，式中的r是物体与地轴的距离，ω是地球自转的角速度．这个向心力来自哪里?只能来自地球对物体的引力F，它是引力F的一个分力如右图，引力F的另一个分力才是物体的重力mg．

在不同纬度的地方，物体做匀速圆周运动的角速度ω相同，而圆周的半径r不同，这个半径在赤道处最大，在两极最小(等于零)．纬度为α处的物体随地球自转所需的向心力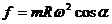 (R为地球半径)，由公式可见，随着纬度升高，向心力将减小，在两极处Rcosα＝0，f＝0．作为引力的另一个分量，即重力则随纬度升高而增大．在赤道上，物体的重力等于引力与向心力之差．即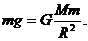．在两极，引力就是重力．但由于地球的角速度很小，仅为10^－5rad／s数量级，所以mg与F的差别并不很大．

在不考虑地球自转的条件下，地球表面物体的重力这是一个很有用的结论．

从图中还可以看出重力mg一般并不指向地心，只有在南北两极和赤道上重力mg才能向地心．

同样，根据万有引力定律知道，在同一纬度，物体的重力和重力加速度g的数值，还随着物体离地面高度的增加而减小．

若不考虑地球自转，地球表面处有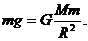，可以得出地球表面处的重力加速度．

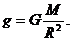在距地表高度为h的高空处，万有引力引起的重力加速度为g＇，由牛顿第二定律可得：

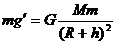　即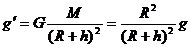

如果在h＝R处，则g＇＝g／4．在月球轨道处，由于r＝60R，所以重力加速度g＇＝ g／3600．

重力加速度随高度增加而减小这一结论对其他星球也适用．

例3、某行星自转一周所需时间为地球上的6h，在这行星上用弹簧秤测某物体的重量，在该行量赤道上称得物重是两极时测得读数的90%，已知万有引力恒量G＝6.67×10^－11N·m²／kg²，若该行星能看做球体，则它的平均密度为多少?

[解析]在两极，由万有引力定律得　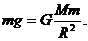　　 ①

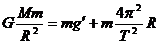在赤道　 ②

依题意mg＇=O.9mg　　 ③

由式①②③和球体积公式联立解得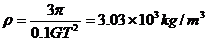

4．注意领会卡文迪许实验设计的巧妙方法．

由万有引力定律表达式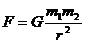可知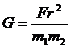，，要测定引力常量G，只需测出两物体m₁、m₂间距离r及它们间万有引力F即可．由于一般物体间的万有引力F非常小，很难用实验的方法显示并测量出来，所以在万有引力定律发现后的百余年间，一直没有测出引力常量的准确数值．

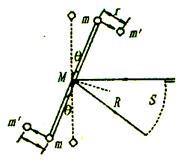
卡文迪许巧妙的扭秤实验通过多次“放大”的办法解决了这一问题．图是卡文迪许实验装置的俯视图．

首先，图中固定两个小球m的r形架，可使m、m’之间微小的万有引力产生较大的力矩，使金属丝产生一定角度的偏转臼，这是一次“放大”效应．

其次，为了使金属丝的微小形变加以“放大”，卡文迪许用从1发出的光线射到平面镜M上，在平面镜偏转θ角时，反射光线偏转2θ角，可以得出光点在刻度尺上移动的弧长s＝2θR，增大小平面镜M到刻度尺的距离R，光点在刻度尺上移动的弧长S就相应增大，这又是一次“放大”效应．由于多次巧妙“放大”，才使微小的万有引力显示并测量出来．除“放大法”外，物理上观察实验效果的方法，还包括“转换法”、“对比法”等．

深刻认识卡文迪许实验的意义

(1)卡文迪许通过改变质量和距离，证实了万有引力的存在及万有引力定律的正确性．

(2)第一次测出了引力常量，使万有定律能进行定量计算，显示出真正的实用价值．

(3)标志着力学实验精密程度的提高，开创了测量弱力的新时代．

(4)表明：任何规律的发现总是经过理论上的推理和实验上的反复验证才能完成．

3．万有引力定律的适用条件

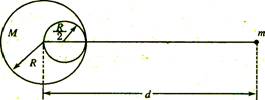
例1、如下图所示，在半径R＝20cm、质量M＝168kg的均匀铜球中，挖去一球形空穴，空穴的半径为要，并且跟铜球相切，在铜球外有一质量m＝1kg、体积可忽略不计的小球，这个小球位于连接铜球球心跟空穴中心的直线上，并且在空穴一边，两球心相距是d＝2m，试求它们之间的相互吸引力．

解： 完整的铜球跟小球m之间的相互吸引力为

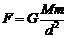
这个力F是铜球M的所有质点和小球m的所有质点之间引力的总合力，它应该等于被挖掉球穴后的剩余部分与半径为娄的铜球对小球m的吸引力　 　　F=F₁+F₂．

式中F₁是挖掉球穴后的剩余部分对m的吸引力，F₂是半径为R／2的小铜球对m的吸引力。因为，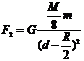

所以挖掉球穴后的剩余部分对小球的引力为F₁＝F－F₂＝2.41×10^－9N

例2、深入地球内部时物体所受的引力

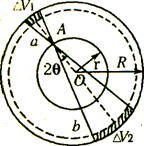假设地球为正球体，各处密度均匀．计算它对球外物体的引力，可把整个质量集中于球心．如果物体深入地球内部，如何计算它所受的引力?

如右图所示，设一个质量为m的物体(可视为质点)在地层内离地心为r的A处．为了计算地球对它的引力，把地球分成许多薄层．设过A点的对顶锥面上两小块体积分别为△V₁、△V₂．当△V₁和△V₂很小时，可以近似看成圆台．

已知圆台的体积公式

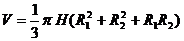
式中R₁和R₂分别是上、下两底面的半径．

当圆台很小很薄时，且H＜＜　a，H＜＜　b时，R₁≈R₂≈R．那么V＝πHR²

根据万有引力定律

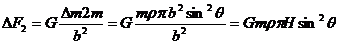
所以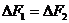，即两小块体积的物体对A处质点的引力大小相等，且方向相反，它们的合力为零．

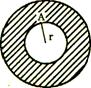
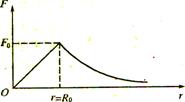当把地球分成许多薄层后，可以看到，位于A点以外的这一圈地层(右图中用斜线表示)对物体的引力互相平衡，相当于对A处物体不产生引力，对A处物体的引力完全由半径为r的这部分球体产生．引力大小为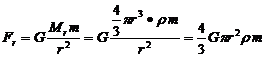

即与离地心的距离成正比．

当物体位于球心时，r=0，则F_r＝O．它完全不受地球的引力．

所以，当一个质量为m的物体从球心(r＝0)逐渐移到球外时，它所受地球的引力F随r的变化关系如右图所示．即先随r的增大正比例地增大；后随r的增大，按平方反比规律减小；当r＝R₀(地球半径)时，引力．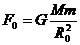

2．万有引力定律的检验

牛顿通过对月球运动的验证，得出万有引力定律，开始时还只能是一个假设，在其后的一百多年问，由于不断被实践所证实，才真正成为一种理论．其中，最有效的实验验证有以下四方面．

⑴．地球形状的预测．牛顿根据引力理论计算后断定，地球的赤道部分应该隆起，形状像个橘子．而笛卡尔根据旋涡假设作出的预言，地球应该是两极伸长的扁球体，像个柠檬．

1735年，法国科学院派出两个测量队分赴亦道地区的秘鲁(纬度φ＝20°)和高纬度处的拉普兰德(φ＝66°)，分别测得两地1°纬度之长为：赤道处是110600m，两极处是111900m．后来，又测得法国附近纬度1°的长度和地球的扁率．大地测量基本证实了牛顿的预言，从此，这场“橘子与柠檬”之争才得以平息．

⑵．哈雷彗星的预报．英国天文学家哈雷通过对彗星轨道的对照后认为，1682年出现的大彗星与1607年、1531年出现的大彗星实际上是同一颗彗星，并根据万有引力算出这个彗星的轨道，其周期是76年．哈雷预言，1758年这颗彗星将再次光临地球．于是，预报彗星的回归又一次作为对牛顿引力理论的严峻考验．

后来，彗星按时回归，成为当时破天荒的奇观，牛顿理论又一次被得到证实．

⑶．海王星的发现．

⑷．万有引力常量的测定．

由此可见，一个新的学说决不是一蹴而就的，也只有通过反复的验证，才能被人们所普遍接受．