
1. 采用多样化的方式学习,体验实际生活与数学的密切联系,提高用数学的意识。
2. 加深对“数与代数”“空间与几何”“统计与概率”内容的理解,体会各部分知识之间的联系,能针对不同的探究题目采取有效的解题策略。
1. 综合运用已有的知识和经验,经过自主探索和合作交流,解决与生活经验密切联系的、具有挑战性和综合性的问题,发展解决问题的能力。
例6 如图,在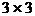 方格内已填好了两个数19和95,可以在其余的方格中填上适当的数,使每一行、每一列、以及每一条对角线上的三个数的和都相等,
方格内已填好了两个数19和95,可以在其余的方格中填上适当的数,使每一行、每一列、以及每一条对角线上的三个数的和都相等,
(1)求x;
(2)在题设的基础上,如果中间的空格上是100,请完成填图。
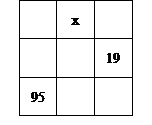
解:(1)设每一行、每一列、每一条对角线的三个数都相等的数是k
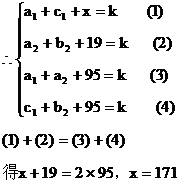
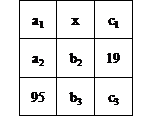
(2)中间填上100,从而不难求每行、每列、每条对角线的三个数的和为300,则其余空格上数字如图。
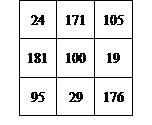
例5 对应实数x,y,设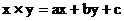 ,等式右边是通常的加法和乘法,且
,等式右边是通常的加法和乘法,且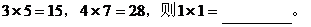
解:由题意,得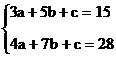
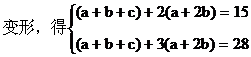
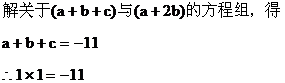
例1 对于任意实数m,等式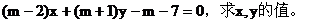
解: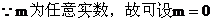
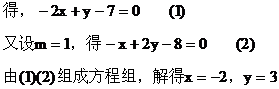
例2 关于x的代数式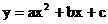 ,当x分别取1,2,-1时,y的值分别是4,7,10,求a,b,c的值。
,当x分别取1,2,-1时,y的值分别是4,7,10,求a,b,c的值。
解:根据题意,得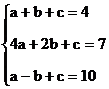
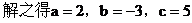
例3 已知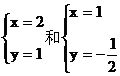 都是关于x,y的某个二元一次方程的解,求这个二元一次方程。
都是关于x,y的某个二元一次方程的解,求这个二元一次方程。
解:设这个二元一次方程为

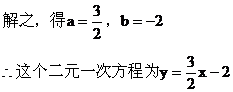
例4 已知等式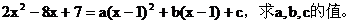
解:由已知条件得
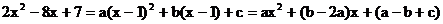
比较对应项的系数,得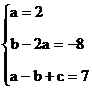
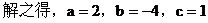
3. 当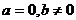 时,方程无解。
时,方程无解。
下面举例予以分析说明。
例1. 解关于x的方程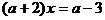
解:当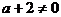 ,即
,即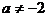 时,方程有唯一解:
时,方程有唯一解: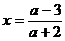
当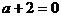 ,即
,即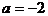 时,原方程可化为:
时,原方程可化为: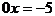 ,方程无解
,方程无解
总结:此方程为什么不存在无穷解呢?因为只有当方程可化为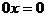 时,方程才能有无穷解,而当
时,方程才能有无穷解,而当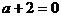 时,
时, ;
;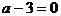 时,
时,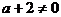 ,a不可能既等于-2又等于3。所以不存在无穷解。
,a不可能既等于-2又等于3。所以不存在无穷解。
例2. 解关于x的方程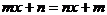
解:原方程可化为
当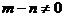 ,即
,即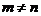 时,方程有唯一解:
时,方程有唯一解: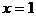
当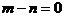 ,即
,即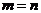 时,方程有无数解
时,方程有无数解
总结:此方程没有无解的情况,因为方程可化为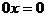 ,而不会出现
,而不会出现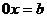 的情形。
的情形。
2. 当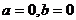 时,方程有无数解;
时,方程有无数解;
1. 当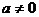 时,方程有唯一解;
时,方程有唯一解;
例5. (2001年江苏无锡中考题)
根据题意,完成下列填空:如图6所示,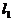 与
与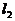 是同一平面内的两条相交直线,它们有一个交点,如果在这个平面内,再画第3条直线
是同一平面内的两条相交直线,它们有一个交点,如果在这个平面内,再画第3条直线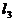 ,那么这3条直线最多可有( )个交点;如果在这个平面内再画第4条直线
,那么这3条直线最多可有( )个交点;如果在这个平面内再画第4条直线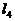 ,那么这4条直线最多可有( )个交点;由此我们可以猜想:在同一平面内,6条直线最多可有( )个交点。n(n为大于1的整数)条直线最多可有( )个交点(用含n的代数式表示)。
,那么这4条直线最多可有( )个交点;由此我们可以猜想:在同一平面内,6条直线最多可有( )个交点。n(n为大于1的整数)条直线最多可有( )个交点(用含n的代数式表示)。
解:(1)画图观察
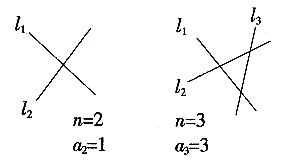 图6
图6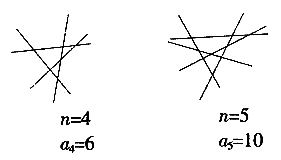
(2)列表归纳
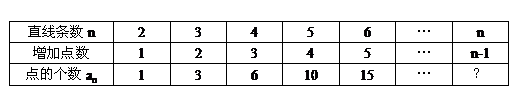
(3)猜想:
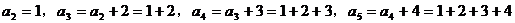 ,……
,……
于是,可猜想n条直线最多可有交点个数为:
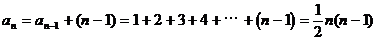
于是,当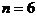 时,
时,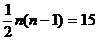 个交点。
个交点。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com