4. 规律探索型--发现数学对象所具有的规律性与不变性的题目。

3. 存在探索型--在一定条件下，需探索发现某种数学关系是否存在。

2. 结论探索型--给定条件，但无明确结论或结论不惟一。

1. 条件探索型--结论明确，而需探索发现使结论成立的条件的题目。

2. 开放型问题

1. 探索型问题

5. 探究存在性型

　　 探究存在性型问题是指在一定的条件下，判断某种数学对象是否存在的问题，它有结论存在和结论不存在两种情形，解答这类问题，一般先对结论作肯定存在的假设，然后由此肯定的假设出发，结合已知条件进行推理论证，若导出矛盾，则否定先前假设；若推出合理的结论，则说明假设正确，由此得出问题的结论。

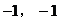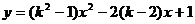　 例16. 已知：点A()在抛物线上

　　 (1)求抛物线的对称轴；

　　 (2)若点B与点A关于抛物线的对称轴对称，问是否存在与抛物线只交于一点B的直线。如果存在，求符合条件的直线；如果不存在，说明理由。

　　 分析：要求过抛物线上点B且仅交抛物线于一点的直线，除了应用判别式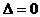解出直线外，不要遗漏与对称轴平行的这一条直线。

　 　解：(1)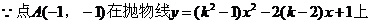

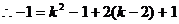
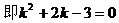
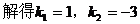
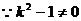
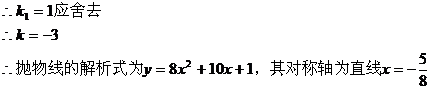
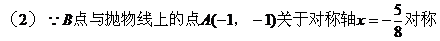
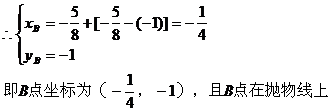
　　 <1>假设存在直线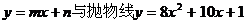只有一个交点

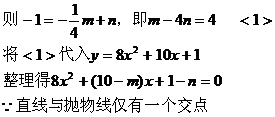
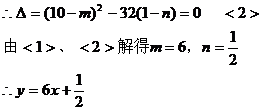
　　 <2> 过B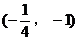且与抛物线的对称轴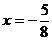平行的直线是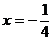，也与抛物线只有一个交点

　　 所以符合条件的直线为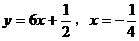

　 例17. 已知抛物线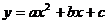，其顶点在x轴的上方，它与y轴交于点C(0，3)与x轴交于点A及点B(6，0)，又知方程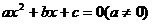两根的平方和等于40。

　　 (1)求此抛物线的解析式；

　　 (2)试问：在此抛物线上是否存在一点P，在x轴上方且使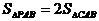。如果存在，求出点P的坐标，如果不存在，说明理由。

　　 解：(1)设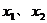是方程的两根

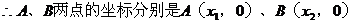
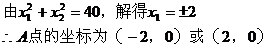
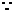　　 抛物线顶点在x轴上方，且与y轴交于点C(0，3)，与x轴交于点B(6，0)

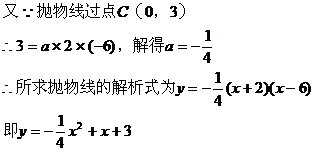
　　 (2)假设抛物线上有一点P(x,y)使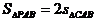

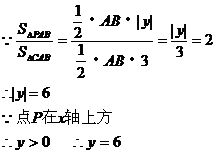
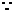　　 抛物线的顶点坐标为(2，4)，y的最大值是4

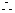　　 点P(x，6)不在抛物线上，即不存在点P在x轴上方且使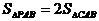

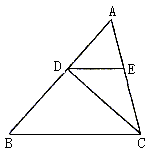
　 例18. 如图，已知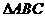中，AB=4，点D在AB边上移动(点D不与A、B重合)，DE//BC交AC于E，连结CD。设。

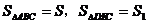　　 (1)当D为AB中点时，求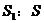的值；

　　 (2)若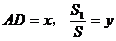，求y关于x的函数关系式及自变量x的取值范围；

　　 (3)是否存在点D，使得成立？若存在，求出D点位置；若不存在，请说明理由。

　　 解：(1)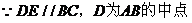

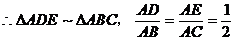
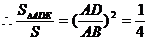
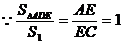
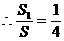
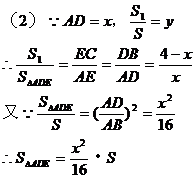
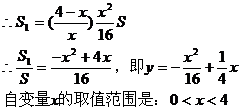
　　 (3)不存在点D，使得成立。理由：假设存在点D，使得成立，那么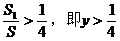

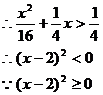
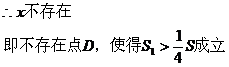
　　6. 实验操作型

　　 数学不仅是思维科学，也是实验科学，通过实验操作，观察猜想，调整等合情推理，得到数学结论，近年来，各地中考试题常以此来考查学生的数学实践能力和创新能力，这种实验操作形式也是进行科学研究的最基本形式。

　　 例16(北京市西城区2002年中考题)也是实验操作性试题，它先通过学生动手测量，然后自己再作图测量，逐步领悟到一个猜想，最后对猜想加以论证。

　 例19. 取一张矩形的纸进行折叠，具体操作过程如下：

　　 第一步：先把矩形ABCD对折，折痕为MN，如图1；

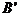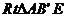　　 第二步：再把B点叠在折痕线MN上，折痕为AE，点B在MN上的对应点为，得，如图2；

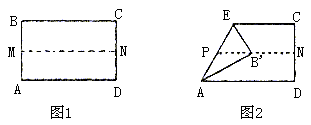
　　 第三步：沿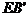线折叠得折痕EF，如图3。

　　 利用展开图4探究：

　　 (1)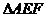是什么三角形？证明你的结论；

　　 (2)对于任一矩形，按照上述方法是否都能折出这种三角形？请说明理由。

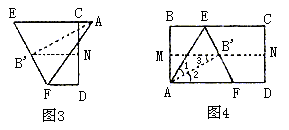
　　 (1)证明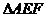：是等边三角形

　　 证法一：由平行线分线段定理得PE=PA

　　 斜边上的中线

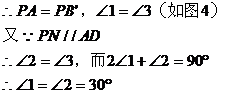
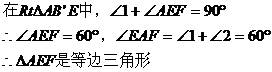
　　 证法二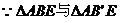：完全重合

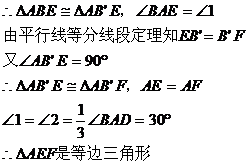
　　 (2)不一定

　　 由以上推证可知当矩形的长恰好等于等边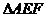的边AF时，即矩形的宽：长=AB：AF=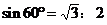时正好能折出。如果设矩形的长为a，宽为b，可知

　　 当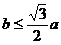时，按此法一定能折出等边三角形；

　　 当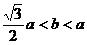时，按此法无法折出完整的等边三角形。

　　 由以上几例看出，解探索性问题实际是经历一次探索、发现、猜想、证明的思维过程，有利于培养和发展创新意识和实践能力。

4. 探究结论型

　　 探求结论型问题是指由给定的已知条件探求相应的结论的问题。解答这类问题的思路是：从所给条件(包括图形特征)出发，进行探索、归纳，大胆猜想出结论，然后对猜想的结论进行推理、证明。

　 例13. 如图，公路上有A、B、C三站，一辆汽车在上午8时从离A站10千米的P地出发向C站匀速前进，15分钟后离A站20千米。

　　 (1)设出发x小时后，汽车离A站y千米，写出y与x之间的函数关系式；

　　 (2)当汽车行驶到离A站150千米的B站时，接到通知要在中午12点前赶到离B站30千米的C站。汽车若按原速能否按时到达？若能，是在几点几分到达；若不能，车速最少应提高到多少？

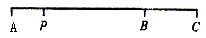
　　 分析：这是生活中的一个实际问题。解第(1)问的关键是读懂题意，求出汽车从P地出发向C站匀速前进的速度。

　　 第(2)问，没有给出明确的结论，需要根据所给的条件探求，汽车行驶到B站后，若按原速行驶，到达C站的时间。

　　 解：(1)汽车从P地出发向C站匀速前进，速度为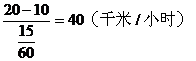

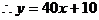
　　 (2)把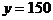代入上式，得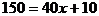

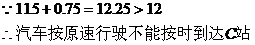
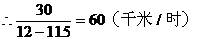
　　 汽车要在中午12点前赶到离B站30千米的C站，车速最少应提高到60千米/时。

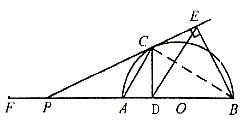
　 例14. 如图，AB为半圆的直径，O为圆心，AB=6，延长BA到F，使FA=AB。若P为线段AF上一个动点(P点与A点不重合)，过P作半圆的切线，切点为C，作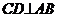，垂足为D。过B点作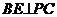，交PC的延长线于点E，连结AC、DE。

　　 (1)判断线段AC、DE所在直线是否平行，并证明你的结论；

　　 (2)设AC为x，AC+BE为y，求y与x的函数关系式，并写出自变量x的取值范围。

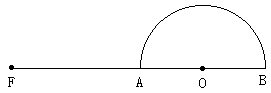
　　 分析：本题是要根据图形的条件探求AC、DE所在直线的位置关系。本题的难点在于P是一个动点，那么AC与DE也始终在随P点的运动而变化。在这种变化中，它们的相对位置是否有一种特定的联系？这就要求我们透过现象，抓住问题的本质，考察其中的必然联系。可由动到静，把动点P设在AF上的任意一个位置，根据题意画出草图，再观察、猜想、推理、判断AC与DE是否平行。

　　 解：(1)依题意画出图形，如图，判断线段AC、DE所在直线互相平行，即AC//DE。

　　 证明：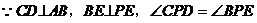

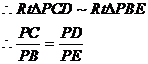
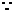　　 PC与⊙O相切于C点，PAB为⊙O的割线

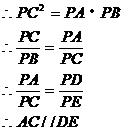
　　 (2)连结BC

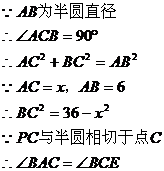
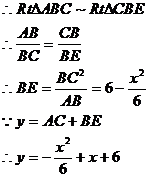
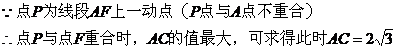
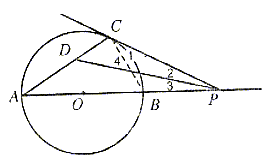
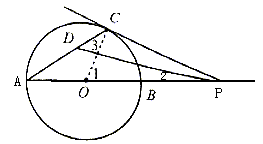
　 例15. 已知：AB为⊙O的直径，P为AB延长线上的一个动点，过点P作⊙O的切线，设切点为C。

　　 (1)当点P在AB延长线上的位置如图1所示时，连结AC，作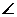APC的平分线，交AC于点D，请你测量出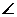CDP的度数；

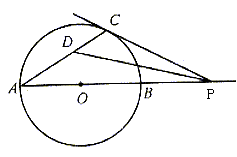
图1

(2)当点P在AB延长线上的位置如图2和图3所示时，连结AC，请你分别在这两个图中用尺规作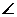APC的平分线(不写作法，保留作图痕迹)，设此角平分线交AC于点D，然后在这两个图中分别测量出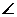CDP的度数；

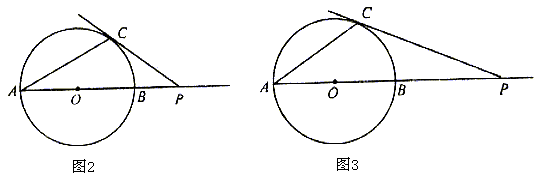
　　 猜想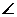：CDP的度数是否随点P在AB延长线上的位置的变化而变化？请对你的猜想加以证明。

　　 解：(1)测量结果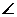：CDP=45^o 　　 (2)(作图略)

　　 图2中的测量结果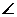：CDP=45^o 　　 图3中的测量结果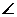：CDP=45^o

　　 猜想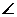：CDP=45^o为确定的值，CDP的度数不随点P在AB延长线上的位置的变化而变化。

　　 证法一：连结BC(如图)

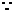　　 AB是⊙O的直径

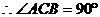
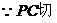　　 ⊙O于点C

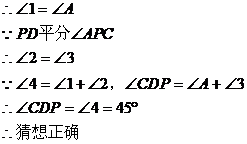
　　 证法二：连结OC(如图)

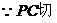　　 ⊙O于点C

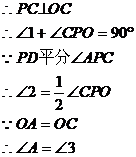
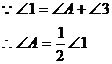
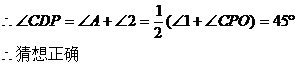
3. 探究条件型

　　 探究条件型问题是指问题中结论明确，而需要完备使结论成立的条件的题目。解答探求条件型问题的思路是，从所给结论出发，设想出合乎要求的一些条件，逐一列出，并进行逻辑证明，从而寻找出满足结论的条件。

　 例10. 已知：如图，在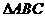中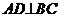，，垂足为D，E、F分别是AB、AC的中点。

　　 (1)EF和AD之间有什么特殊的位置关系？请证明你找到的结论。

　　 (2)要使四边形AEDF是菱形，需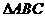满足什么条件？

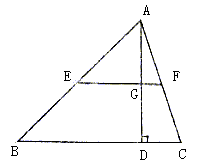
　　 解：(1)EF垂直平分AD

　　 (2)由(1)知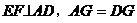

　　 要使四边形AEDF是菱形，只需要

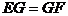
　　 显然需要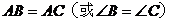满足，即满足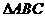是等腰三角形这个条件。

　 例11. 如图，已知点A(0，6)、B(3，0)、C(2，0)、M(0，m)，其中m<6，以M为圆心，MC为半径作圆，则

　　 (1)当m为何值时，⊙M与直线AB相切？

　　 (2)当m=0时，⊙M与直线AB有怎样的位置关系？当m=3时，⊙M与直线AB有怎样的位置关系？

　　 (3)由(2)验证的结果，你是否得到启发，从而说出m在什么范围内取值时，⊙M与直线AB相离？相交？

　　 ((2)、(3)只写结果，不必写过程)

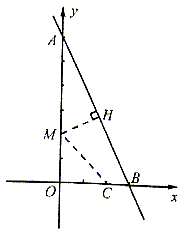
　　 分析：(1)属探求条件型问题，是由给定的结论--以M为圆心，MC长为半径的⊙M与直线AB相切，反溯探究M点的纵坐标应具备的条件。过点M作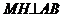，垂足为H，若MH等于半径MC，根据直线与圆相切的判定定理，则⊙M与直线AB相切，再进一步追溯使MH=MC时，M点纵坐标m的值。

　　 解：(1)过点M作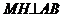，垂足为H，若MH=MC，则以M为圆心、MC长为半径的⊙M与AB相切。

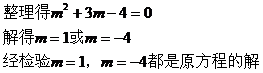
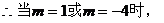　　 ⊙M与直线AB相切

　　 (2)当m=0时，⊙M与直线AB相离；当m=3时，⊙M与直线AB相交

　　 (3)当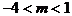时，⊙M与直线AB相离；当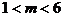或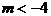时，⊙M与直线AB相交。

　 例12. 当a取什么数值时，关于未知数x的方程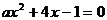只有正实数根？

　　 分析：本题是探究条件的题目，需要从关于x的方程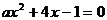只有正实数根出发，考虑a可取的所有值。首先要验证a=0时，方程为一元一次方程，方程是否有正实根；然后再考虑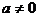，方程为一元二次方程的情况。

　　 解：(1)当a=0时，方程为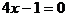

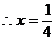
　　 (2)当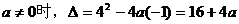

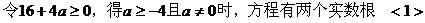
　　 设方程的两个实数根为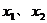

　　 要使方程只有正实数根，由根与系数的关系，需

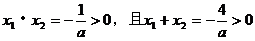
　　 解之，得a<0　　 <2>

　　 由<1>、<2>可得，当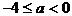时，原方程有两个正实根

综上讨论可知：当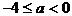时，方程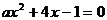只有正实数根