
1. 如图5,过边OB上任意一点D作OA边的平行线DE。
4. 作射线OC,OC就是 AOB的平分线。
AOB的平分线。

证明 因为OD=OE,C是DE的中点,所以OC是等腰 底边DE的中线,也是高线,也是顶角
底边DE的中线,也是高线,也是顶角 AOB的平分线。
AOB的平分线。
注 在学习等腰三角形性质时,可插入该作图方法,使学生加深对等腰三角形底边上的中线,高线,顶角平分线,三线合一的理解。该作图取线段DE的中点C应运用线段垂直平分线的基本作法来解决,培养学生的动手能力,提高基本作图技能。
作法5
3. 取DE的中点C。
2. 连结DE。
1. 如图4,在 AOB的边OA、OB上分别截取OD、OE,使OD=OE。
AOB的边OA、OB上分别截取OD、OE,使OD=OE。
3. 作射线OC,OC就是 AOB的平分线。
AOB的平分线。
证明 由作法,知OQ=OP,OT=OS
所以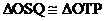
即 PSC=
PSC= QTC
QTC
又 PCS=
PCS= QCT,PS=QT
QCT,PS=QT
所以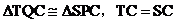
又OT=OS,OC=OC
所以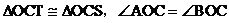
注 该作角平分线的方法,较容易掌握,切实可行,该作图证明,用到了三角形全等的SAS、AAS、SSS等定理,须引导学生善于找出对应的三角形关系。
作法4
2. 连结PT、QS相交于点C。
1. 如图3,在 AOB两边OA、OB上分别截取OQ=OP,OT=OS。
AOB两边OA、OB上分别截取OQ=OP,OT=OS。
2. 分别过点M、N作OA、OB的垂线,交点为P。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com