2. 求证：顺次连结等腰梯形上、下底的中点和两对角线的中点所构成的四边形是菱形。

1. 求证：顺次连结等腰梯形各边中点所构成的四边形是菱形。

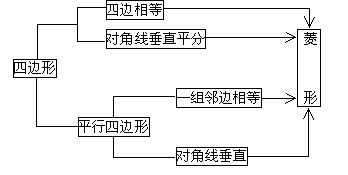
4. 对角线互相垂直平分的四边形是菱形

　　 例4　 已知：如图4，中，BAC的平分线交BC于点D，E是AB上一点，且AE=AC，EF//BC交AD于点F。

　　 求证：四边形CDEF是菱形。

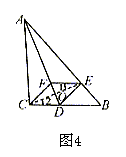
　　 证明：连结CE交AD于点O

　　 因为AC=AE

　　 所以为等腰三角形

　　 因为AO平分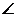CAE

　　 所以，且OC=OE

　　 因为EF//CD，

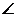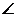　　 所以1=2

　　 所以OF=OD

　　 于是CE垂直平分DF

　　 所以四边形CDEF是菱形

　　 总结以上，得到下表

　　 练习：

3. 对角线互相垂直的平行四边形是菱形

　　 例3　 已知：如图3，梯形ABCD中，AD//BC，对角线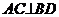，M、N为底边BC的三等分点，且BC=3AD，AM与BD交于点G，AC与DN交于点H。求证：四边形AGHD是菱形。

　　 证明：因为BC=3AD

　　 M、N是BC的三等分点

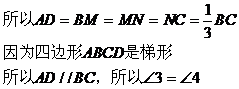
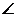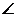　　 又1=2

　　 所以四边形AGHD是平行四边形

　　 又，所以四边形AGHD是菱形。

2. 邻边相等的平行四边形一定是菱形

　　 例2　 已知：如图2，在等腰梯形ABCD中，AD//BC，M、N分别是AD、BC的中点，E、F分别是BM、CM的中点。求证：四边形MENF是菱形。

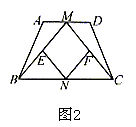
　　 证明：因为E是BM的中点，N是BC的中点，F是CM的中点

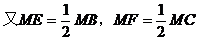
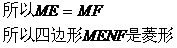
1. 证明四边形的四条边相等

　　 例1　 已知：如图1，C是线段BD上一点，和都是等边三角形，R、F、G、H分别是四边形ABDE各边的中点。求证：四边形RFGH是菱形。

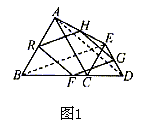
　　 证明：连结AD、BE

　　 因为和都是等边三角形

　　 所以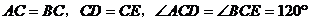

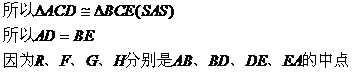
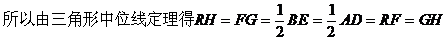
　　 故四边形RFGH是菱形

　　 例3. 设。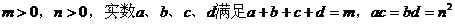

　　 试求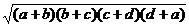：的值(用含m、n的式子表示)。

　　 分析：

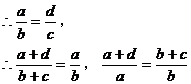
　　 运用等比性质可得：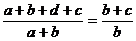

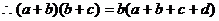
　　 而条件中又告知：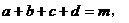

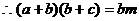
　　 运用同样的方法可得：

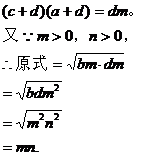
　　 编者语：以上三例我们用等比性质，很简捷地得出了结果。如用常规办法，每题都很繁杂。但是用此法的关键是要熟记等比性质，且能灵活应用。

　　 例1. 化简

　　 分析：注意到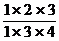

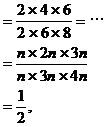
　　 所以由等比性质可得原式的被开方数为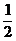，故原式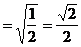

　　 例2. 化简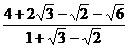

　　 分析：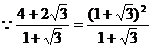

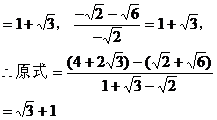
3. 作射线OC，OC就是AOB的平分线。

　　 分析　 该作图联系了两直线平行内错角相等和等腰三角形两底角相等的性质。

　　 证明　 由作法，知DC//OA

　　 所以DCO=AOC

　　 又DC=DO

　　 所以DCO=DOC，AOC=DOC

　 以上几种角平分线的尺规作图方法，都是由几何证明题改编而成的，可激发同学们学习几何的兴趣，开拓思路，增进知识的横纵联系，巩固基础，培养动脑动手能力。

2. 在DE上取DC=DO。