
6.设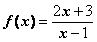 ,函数
,函数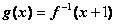 的图象与
的图象与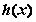 的图象关于直线
的图象关于直线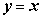 对称,则
对称,则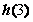 的值为
的值为
A.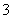 B.
B.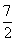 C.
C.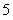 D.
D.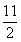
5.将函数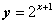 的图象按向量
的图象按向量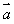 平移得到函数
平移得到函数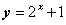 的图象,则
的图象,则
A.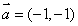 B.
B.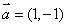 C.
C.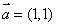 D.
D.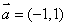
4、函数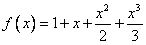 与
与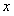 轴交点的个数是(
)
轴交点的个数是(
)
A、0 B、1 C、2 D、3
3、 已知p:关于x的不等式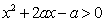 的解集是R;
的解集是R;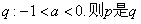 的( )
的( )
A.充分非必要条件 B.必要非充分条件
C.充要条件 D.既非充分又非必要条件
2.不等式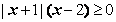 的解集为
的解集为
A.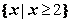 B.
B.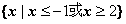
C.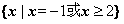 D.
D.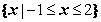
1.设全集
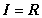 ,集合
,集合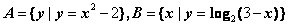 ,则
,则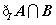 等于
等于
A.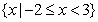 B.
B. C.
C.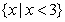 D.
D.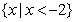
2.要从全班学生中随机抽选8人去参加一项活动,分别用抽签法和随机数表法进行抽选
并写出过程。
1.某市的3个区共有高中学生20000人,且3个区的高中学生人数之比为2:3:5,现要
用分层抽样方法从所有学生中抽取一个容量为200的样本,这3个区分别应抽取多少人?
2.分层抽样
一个单位的职工有500人,其中不到35岁的有125人,35岁至49岁的有280人,50岁以上的有95人,为了了解这个单位职工与身体状况有关的某项指标,要从中抽取100名职工作为样本,职工年龄与这项指标有关,应该怎样抽取?
为了使抽出的100名职工更充分地反映单位职工的整体情况,在各个年龄段可按这部分职工人数与职工总数的比进行抽样。
因为抽取人数与职工总数的比为100 :500=1 :5
:500=1 :5
所以在各年龄段抽取的职工人数依次是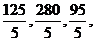
 即25,56,19
即25,56,19
在各个年龄段分别抽取时,可采用前面介绍的简单随机抽样的方法,将各年龄段抽取的职工合在一起,就是所要抽取的100名职工。
像这样当已知总体由差异明显的几部分组成时,为了使样本更充分地反映总体的情况,常将总体分成几部分,然后按照各部分所占的比进行抽样,这种抽取叫做分层抽样,其中所分成的各部分叫做层。
可以看到,由于各部分抽取的个体数与这一部分个体数的比等于样本容量与总体的个体数的比,分层抽样时,每一个个体被抽到的概率都是相等的。
由于分层抽样充分利用了已知信息,使样本具有较好的代表性,而且在各层抽样时,可以根据具体情况采取不同的抽样方法,因此分层抽样在实践中有着广泛的应用。
以上我们简单介绍了简单随机抽样和分层抽样,这两种抽样方法的共同特点是:在整个抽样过程中每个个体被抽取的概率相等。简单随机抽样是最基本的抽样方法,当总体由差异明显的几部分组成,采取分层抽样时,其中各层的抽样常采用简单随机抽样。
小结:了解简单随机抽样与分层抽样的概率,会用简单随机抽样与分层抽样从总体中抽取样本。
作业:
1.简单随机抽样:
假定一个小组有6个学生,要通过逐个抽取的方法从中取3个学生参加一项活动,第1次抽取时每个被抽到的概率是___,第2次抽取时,余下的每个被抽到的概率都是__,第3次抽取时,余下的每个被抽到的概率都是__。
每次抽取时各个个体被抽到的概率是相等的,那么在整个抽样过程中每个个体被抽到的概率是否确实相等?
例如,从含有6个体的总体中抽取一个容量为2的样本,在整个抽样过程中,总体中的任意一个个体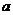 ,在第一次抽取时,它被抽到的概率是__;若它第1次未被抽到而第2次被抽到的概率是____,由于个体
,在第一次抽取时,它被抽到的概率是__;若它第1次未被抽到而第2次被抽到的概率是____,由于个体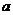 第1次被抽到与第2次被抽到是___(填互斥,独立)事件,根据___事件的概率__公式,在整个抽样过程中,个体
第1次被抽到与第2次被抽到是___(填互斥,独立)事件,根据___事件的概率__公式,在整个抽样过程中,个体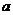 被抽到的概率P=_______。又由于个体
被抽到的概率P=_______。又由于个体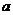 的任意性,说明在抽样过程中每个体被抽到的概率相等,都是__。
的任意性,说明在抽样过程中每个体被抽到的概率相等,都是__。
一般地,设一个总体的个体总数为N,如果通过逐个抽取的方法从中抽取样本,且每次抽取时各个个体被抽到的概率相等,就称这样的抽样为简单随机抽样。
事实上:用简单随机抽样的方法从个体数为N的总体中逐次抽取一个容量为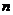 的样本,那么每次抽取时各个个体被抽到的概率相等,依次是
的样本,那么每次抽取时各个个体被抽到的概率相等,依次是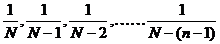 ,且在整个抽样过程中每个个体被抽到概率都等于
,且在整个抽样过程中每个个体被抽到概率都等于 。
。
由于简单随机抽样体现了抽样的客观性和公平性,且这种抽样方法比较简单,所以成为一种基本的抽样方法。如何实施简单抽样呢?下面介绍两种常用方法
(1)抽签法
先将总体中的所有个体编号(号码可以从1到N),并把号码写在形状、大小相同的号签上,号签可以用小球、卡片、纸条等制作,然后将这些号签放在同一个箱子里,进行均匀搅拌,抽签时,每次从中抽出1个号签,连续抽取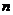 次,就得到一个容量为
次,就得到一个容量为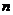 的样本,对个体编号时,也可以利用已有的编号,例如从全班学生中抽取样本时,可以利用学生的学号、座位号等。
的样本,对个体编号时,也可以利用已有的编号,例如从全班学生中抽取样本时,可以利用学生的学号、座位号等。
抽签法简便易行,当总体的个体数不多时,适宜采用这种方法。
(2)随机数表法
下面举例说明如何用随机数表来抽取样本。
为了检验某种产品的质量,决定从40件产品中抽取10件进行检查,在利用随机数表抽取这个样本时,可以按下面的步骤进行:
第一步,先将40件产品编号,可以编为00,01,02,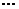 ,38,39。
,38,39。
第二步,在附录1随机数表中任选一个数作为开始,例如从第8行第5列的数59开始,为便于说明,我们将附录1中的第6行至第10行摘录如下。
16 22 77 94 39 49 54 43 54 82 17 37 93 23 78 87 35 20 96 43 84 26 34 91 64
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76
63 01 63 78 59 16 95 55 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 79
33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54
57 60 86 32 44 09 47 27 96 54 49 17 46 09 62 90 52 84 77 27 08 02 73 43 28
第三步,从选定的数59开始向右读下去,得到一个两位数字号码59,由于59>39,将它去掉;继续向右读,得到16,将它取出;继续下去,又得到19,10,12,07,39,38,33,21,随后的两位数字号码是12,由于它在前面已经取出,将它去掉,再继续下去,得到34。至此,10个样本号码已经取满,于是,所要抽取的样本号码是
16 19 10 12 07 39 38 33 21 34
注 将总体中的N个个体编号时可以从0开始,例如N=100时编号可以是00,01,02,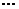
99,这样总体中的所有个体均可用两位数字号码表示,便于运用随机数表。
当随机地选定开始读数的数后,读数的方向可以向右,也可以向左、向上、向下等等。
在上面每两位、每两位地读数过程中,得到一串两位数字号码,在去掉其中不合要求和与前面重复的号码后,其中依次出现的号码可以看成是依次从总体中抽取的各个个体的号码。由于随机数表中每个位置上出现哪一个数字是等概率的,每次读到哪一个两位数字号码,即从总体中抽到哪一个个体的号码也是等概率的。因而利用随机数表抽取样本保证了各个个体被抽取的概率相等。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com