
2. 一种新发现的细菌质粒中有a、b、c等基因,右图表示用限制性内切酶处理后得到的片段。下列有关叙述中不正确的是
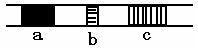 A.基因a、b、c在生命活动过程中选择性表达
A.基因a、b、c在生命活动过程中选择性表达
B.基因a控制合成的蛋白质含有m个氨基酸,比水稻中控制
合成含有m个氨基酸的蛋白质的基因长度要短很多
C.若利用某药物阻止基因a的表达,则基因b、c也不能表达
D.组成基因a、b、c的基本单位相同,而且基因a、b、c中都有RNA聚合酶的结合位点
1.下图显示四种细菌(1、2、3、4)对琼脂板 上的抗生素X的不同反应,请问哪种细菌对 抗生素X的抗药性最强
抗生素X的抗药性最强
A.细菌1
B.细菌2
C.细菌3
D.细菌4
22、解:(Ⅰ)当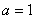 时,
时,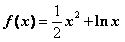 ,
,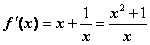 ;………2分
;………2分
对于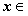 [1,e],有
[1,e],有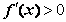 ,∴
,∴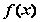 在区间[1,e]上为增函数,…3分
在区间[1,e]上为增函数,…3分
∴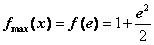 ,
,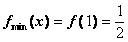 .……………………………5分
.……………………………5分
(Ⅱ)令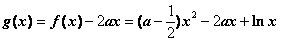 ,
,
则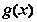 的定义域为(0,+∞).…………6分
的定义域为(0,+∞).…………6分
在区间(1,+∞)上函数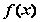 的图象恒在直线
的图象恒在直线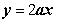 下方等价于
下方等价于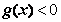 在区间(1,+∞)上恒成立.
在区间(1,+∞)上恒成立.
∵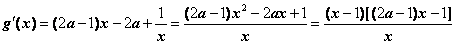
① 若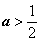 ,令
,令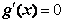 ,得极值点
,得极值点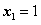 ,
,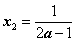 ,
,
当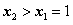 ,即
,即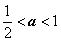 时,在(
时,在(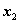 ,+∞)上有
,+∞)上有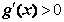 ,
,
此时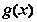 在区间(
在区间(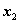 ,+∞)上是增函数,并且在该区间上有
,+∞)上是增函数,并且在该区间上有
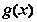 ∈(
∈(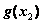 ,+∞),不合题意;………………………………………8分
,+∞),不合题意;………………………………………8分
当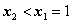 ,即
,即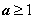 时,同理可知,
时,同理可知,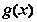 在区间(1,+∞)上,有
在区间(1,+∞)上,有
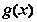 ∈(
∈(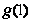 ,+∞),也不合题意;………………………………………9分
,+∞),也不合题意;………………………………………9分
② 若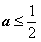 ,则有
,则有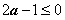 ,此时在区间(1,+∞)上恒有
,此时在区间(1,+∞)上恒有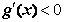 ,
,
从而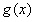 在区间(1,+∞)上是减函数;……………………………………10分
在区间(1,+∞)上是减函数;……………………………………10分
要使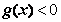 在此区间上恒成立,只须满足
在此区间上恒成立,只须满足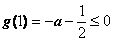
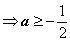 ,
,
由此求得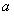 的范围是[
的范围是[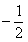 ,
,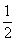 ].
].
综合①②可知,当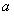 ∈[
∈[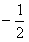 ,
,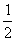 ]时,
]时,
函数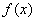 的图象恒在直线
的图象恒在直线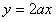 下方. ………………12分
下方. ………………12分
21、解:(Ⅰ)已知式即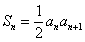 ,故
,故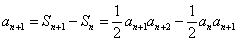 .
.
因为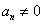 ,当然
,当然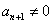 ,所以
,所以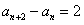
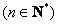 .
.
由于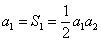 ,且
,且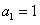 ,故
,故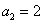 .
.
于是 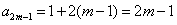 ,
,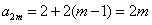 ,
,
所以 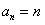
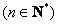 .
……………4分
.
……………4分
(Ⅱ)由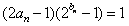 ,得
,得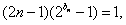
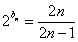 ,
,
故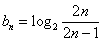 .从而
.从而 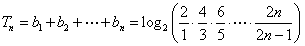 .
.
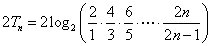
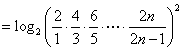
因此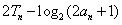
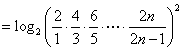
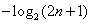
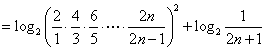
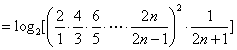 .
.
设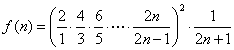 ,
,
则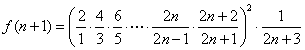 ,
,
故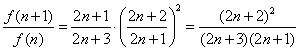
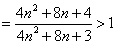 ,
,
注意到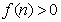 ,所以
,所以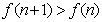 .
.
特别地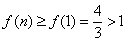 ,从而
,从而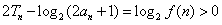 .
.
所以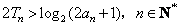 .
………………12分
.
………………12分
22.(本小题满分12分)已知函数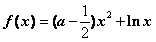 .(
.(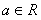 )
)
(Ⅰ)当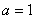 时,求
时,求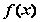 在区间[1,e]上的最大值和最小值;
在区间[1,e]上的最大值和最小值;
(Ⅱ)若在区间(1,+∞)上,函数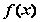 的图象恒在直线
的图象恒在直线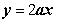 下方,求
下方,求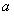 的取值范围.
的取值范围.

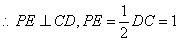 又平面
又平面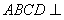 平面
平面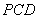
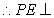 平面
平面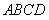 。
。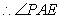 就是
就是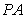 与平面
与平面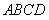 所成的角。……6分
所成的角。……6分
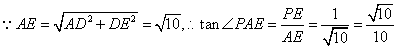 ………………………7分
………………………7分
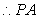 与平面
与平面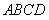 所成的角的正切值为
所成的角的正切值为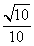 ………8分
………8分
(3)解:当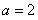 时,
时,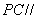 平面
平面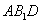 ………9分由
………9分由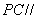 平面
平面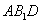 ,
,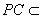 平面
平面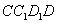 ,平面
,平面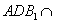 平面
平面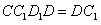
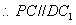 ,又
,又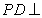 平面
平面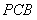 ,
,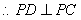 ,因而
,因而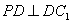 …10分又
…10分又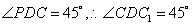 即
即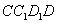 是正方形,
是正方形,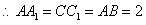 …………………12分
…………………12分
21、(本小题满分12分)
已知数列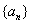 的前
的前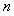 项和为
项和为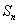 ,且
,且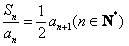 ,其中
,其中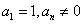 .
.
(Ⅰ)求数列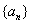 的通项公式;
的通项公式;
(Ⅱ)设数列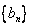 满足
满足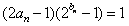 ,
,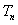 为
为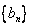 的前
的前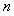 项和,求证:
项和,求证:
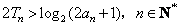 ;
;
20.(本小题满分12分)
在如图组合体中,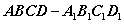 是一个长方体,
是一个长方体, 是一个四棱锥。
是一个四棱锥。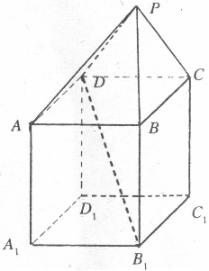
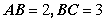 ,
,
点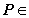 平面
平面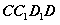 ,且
,且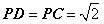 。
。
(1)证明: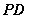
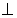 平面
平面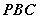 ;
;
(2)求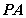 与平面
与平面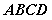 所成的角的正切值;
所成的角的正切值;
(3)若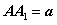 ,当
,当 为何值时,
为何值时,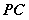
 平面
平面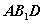 。
。
19、(本题满分12分)
若点P是椭圆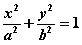 上一点,
上一点,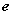 为离心率,
为离心率,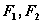 分别为椭圆的左右焦点,若
分别为椭圆的左右焦点,若
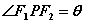 ,求证
,求证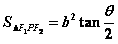
18.(本小题满分12分)
某公司拟资助三位大学生自主创业,现聘请两位专家,独立地对每位大学生的创业方案进行评审.假设评审结果为“支持”或“不支持”的概率都是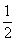 .若某人获得两个“支持”,则给予10万元的创业资助;若只获得一个“支持”,则给予5万元的资助;若未获得“支持”,则不予资助.求:
.若某人获得两个“支持”,则给予10万元的创业资助;若只获得一个“支持”,则给予5万元的资助;若未获得“支持”,则不予资助.求:
(1)该公司的资助总额为零的概率
(2)该公司资助总额超过15万元的概率
17、(本小题满分10分)
在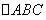 中,
中,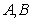 为锐角,角
为锐角,角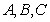 所对应的边分别为
所对应的边分别为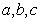 ,且
,且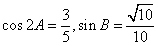
(I)求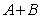 的值;(II)若
的值;(II)若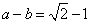 ,求
,求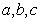 的值。
的值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com