
3.大自然有晴天雨天,这是人所共知的。其实,你想过没有,不只是大自然有晴天雨天,一个人的生命里同样也会有晴天雨天……
请以“我的晴天雨天”为话题作文,题目自拟,立意自定,文体不限,不少于800字。
[写作提示]
看到话题以后,我们首先要对话题进行审读、定位。“我的晴天雨天”这个话题,可以从两个层面去理解:一是自然景物,二是生命意义。如果从自然景物的层面去写,就很容易写成纯自然界的晴天雨天,那将意义不大,升华不出寓意深远的主旨,我们应该尽量避免,而要努力地从第二个层面--生命意义去写作。把生命意义的晴天雨天写足写够,自然就有可能写出佳作。
那么,什么是生命意义的晴天雨天呢?具体说来,生命意义的雨天,可以理解为人生中的坎坷、磨难、挫折、痛苦、打击、失败,等等。生活中,谁的人生会一帆风顺呢?生命意义的晴天,又可以具体理解为高兴、快乐、顺利、上进、收获、成功等。再卑微的生命,也会有高兴、快乐、成功等。从第二个层面去挖掘、生发,是比较容易写出好作文来的。
此外,还必须注意的一点是,话题中还有一个“我”字,它限定了人物范围,暗示着写自己的亲历、亲受,而避免生拉硬扯,无情造文。
图画作文
10. 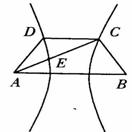 如图,已知梯形ABCD中
如图,已知梯形ABCD中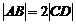 ,点E分有向线段
,点E分有向线段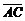 所成的比为
所成的比为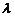 ,双曲线过C、D、E三点,且以A、B为焦点.当
,双曲线过C、D、E三点,且以A、B为焦点.当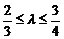 时,求双曲线离心率
时,求双曲线离心率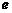 的取值范围.
的取值范围.
解:如图,以AB的垂直平分线为y轴,直线AB为x轴,建立直角坐标系xoy,则CD⊥y轴.
因为双曲线经过点C、D,且以A、B为焦点,由双曲线的对称性知C、D关于x轴对称.依题意,记A(-c,0),C(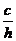 ,h),E(x0, y0),其中c=
,h),E(x0, y0),其中c=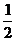 |AB|为双曲线的半焦距,h是梯形的高.
|AB|为双曲线的半焦距,h是梯形的高.
由定比分点坐标公式得
x0=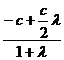 =
= 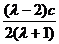 ,
,
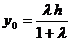 .
.
设双曲线的方程为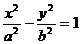 ,则离心率
,则离心率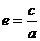 .
.
由点C、E在双曲线上,将点C、E的坐标和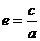 代入双曲线方程得
代入双曲线方程得
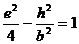 ,
①
,
①
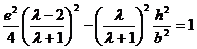 . ②
. ②
由①式得 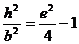 ,
③
,
③
将③式代入②式,整理得
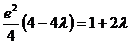 ,
,
故 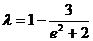
由题设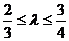 得,
得,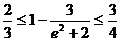 .
.
解得 .
.
所以双曲线的离心率的取值范围为 .
.
[探索题]如图,在双曲线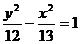 的上支有三点
的上支有三点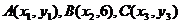 ,它们与点F(0,5)的距离成等差数列。
,它们与点F(0,5)的距离成等差数列。
(1)
求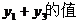
(2) 证明:线段AC的垂直平分线经过某一定点,并求此点坐标
解:(1)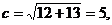 故F双曲线的焦点,设准线为
故F双曲线的焦点,设准线为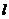 ,离心率为
,离心率为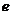 ,
,
由题设有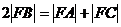 ①
①
分别过A、B、C作x轴的垂线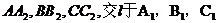 ,则由双曲线的第二定义有
,则由双曲线的第二定义有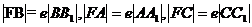 ,
,
代入①式,得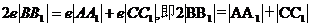 ,
,
于是两边均加上准线与x轴距离的2倍,有
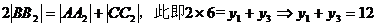
AC的中垂线方程为
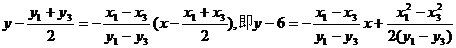 (2)由于A、C在双曲线上,所以有
(2)由于A、C在双曲线上,所以有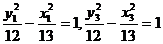
相减得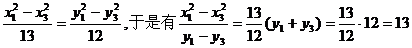
故(2)式化为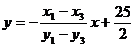 ,易知此直线过定点
,易知此直线过定点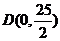 。
。
思维点拨:利用第二定义得焦半径,可使问题容易解决,中垂线过弦AC的中点,中点问题往往把A、C的坐标代入方程,两式相减、变形,即可解决问题。
9.
已知椭圆具有性质:若M、N是椭圆C上关于原点对称的两个点,点P是椭圆上任意一点,当直线PM、PN的斜率都存在,并记为kPM、kPN时,那么kPM与kPN之积是与点P位置无关的定值 试对双曲线C′:
试对双曲线C′: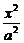 -
-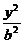 =1写出具有类似特性的性质,并加以证明
=1写出具有类似特性的性质,并加以证明
解:类似的性质为若MN是双曲线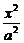 -
-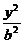 =1上关于原点对称的两个点,点P是双曲线上任意一点,当直线PM、PN的斜率都存在,并记为kPM、kPN时,那么kPM与kPN之积是与点P位置无关的定值
=1上关于原点对称的两个点,点P是双曲线上任意一点,当直线PM、PN的斜率都存在,并记为kPM、kPN时,那么kPM与kPN之积是与点P位置无关的定值
设点M的坐标为(m,n),
则点N的坐标为(-m,-n),
其中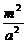 -
-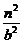 =1
=1
又设点P的坐标为(x,y),
由kPM=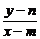 ,kPN=
,kPN=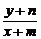 ,
,
得kPM·kPN=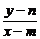 ·
·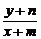 =
=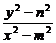 ,
,
将y2=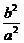 x2-b2,n2=
x2-b2,n2=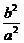 m2-b2,代入得
kPM·kPN=
m2-b2,代入得
kPM·kPN=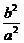
点评:本题主要考查椭圆、双曲线的基本性质,考查类比、归纳、探索问题的能力 它是一道综合椭圆和双曲线基本知识的综合性题目,对思维能力有较高的要求
它是一道综合椭圆和双曲线基本知识的综合性题目,对思维能力有较高的要求
8.已知双曲线的方程为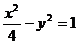 , 直线
, 直线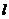 通过其右焦点F2,且与双曲线的右支交于A、B两点,将A、B与双曲线的左焦点F1连结起来,求|F1A|·|F1B|的最小值
通过其右焦点F2,且与双曲线的右支交于A、B两点,将A、B与双曲线的左焦点F1连结起来,求|F1A|·|F1B|的最小值
解:设A(x1,y1),B(x2,y2),
A到双曲线的左准线x= ─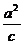 = ─
= ─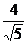 的距离d=|x1+
的距离d=|x1+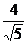 |=x1+
|=x1+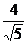 ,
,
由双曲线的定义,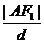 =e=
=e=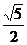 ,
,
∴|AF1|=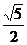 (x1+
(x1+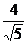 )=
)=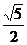 x1+2,
x1+2,
同理,|BF1|=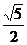 x2+2,
x2+2,
∴|F1A|·|F1B|=(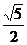 x1+2)(
x1+2)(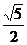 x2+2)=
x2+2)=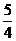 x1x2+
x1x2+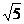 (x1+x2)+4 (1)
(x1+x2)+4 (1)
双曲线的右焦点为F2(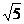 ,0),
,0),
(1)当直线的斜率存在时设直线AB的方程为:y=k(x─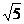 ),
),
由 消去y得 (1─4k2)x2+8
消去y得 (1─4k2)x2+8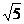 k2x─20k2─4=0,
k2x─20k2─4=0,
∴x1+x2=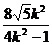 , x1x2= ─
, x1x2= ─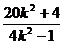 ,
,
代入(1)整理得
|F1A|·|F1B|=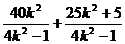 +4=
+4=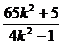 +4
+4
=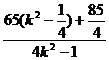 +4=
+4=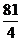 +
+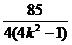
∴|F1A|·|F1B|>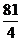 ;
;
(2)当直线AB垂直于x轴时,容易算出|AF2|=|BF2|=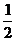 ,
,
∴|AF1|=|BF1|=2a+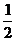 =
=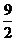 (双曲线的第一定义), ∴|F1A|·|F1B|=
(双曲线的第一定义), ∴|F1A|·|F1B|=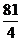
由(1), (2)得:当直线AB垂直于x轴时|F1A|·|F1B| 取最大值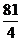
7. (2006江苏)已知三点P(5,2)、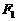 (-6,0)、
(-6,0)、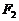 (6,0).
(6,0).
(Ⅰ)求以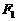 、
、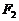 为焦点且过点P的椭圆的标准方程;
为焦点且过点P的椭圆的标准方程;
(Ⅱ)设点P、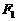 、
、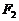 关于直线y=x的对称点分别为
关于直线y=x的对称点分别为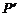 、
、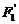 、
、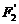 ,求以
,求以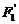 、
、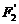 为焦点且过点
为焦点且过点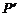 的双曲线的标准方程。
的双曲线的标准方程。
解:(I)由题意,可设所求椭圆的标准方程为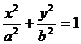 (a>b>0),
(a>b>0),
其半焦距c=6
2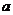 =|PF1|+|PF2|=
=|PF1|+|PF2|=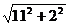 +
+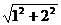 =6
=6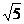
∴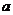 =3
=3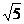 ,b2=a2-c2=45-36=9
,b2=a2-c2=45-36=9
所以所求椭圆的标准方程为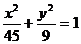
(II)点P(5,2)、F1(-6,0)、F2(6,0)关于直线y=x的对称点分别为P´(2,5)、F1´(0,-6),F2´(0,6)
设所求双曲线的标准方程为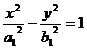 (a1>0,b1>0).
(a1>0,b1>0).
由题意知,半焦距c1=6,
2a1=||P´F1´|-|P´F2´||=|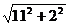 -
-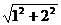 |=4
|=4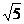 .
.
∴a1=2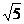 ,b
,b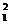 =c
=c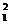 -a
-a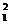 =36-20=16.
=36-20=16.
所以所求双曲线的标准方程为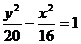
6. ||PF1|-|PF2||=6,cos∠F1PF2=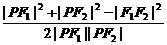
=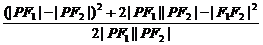 =
=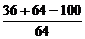 =0
=0
∴∠F1PF2=90°
[解答题]
6.已知双曲线的方程是16x2-9y2=144,F1和F2是双曲线的左、右焦点,点P在双曲线上,且|PF1|·|PF2|=32,求∠F1PF2的大小
简答提示:1-3.CDC; 4. 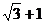 ; 5.
; 5.
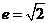 ;
;
5.(2005山东)设双曲线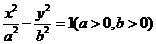 的右焦点为
的右焦点为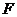 ,右准线
,右准线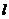 与两条渐近线交于P、
与两条渐近线交于P、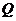 两点,如果
两点,如果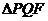 是直角三角形,则双曲线的离心率e=________.
是直角三角形,则双曲线的离心率e=________.
4.(2005福建)已知F1、F2是双曲线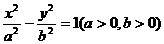 的两焦点,以线段F1F2为边作正三角形MF1F2,若边MF1的中点在双曲线上,则双曲线的离心率是_____
的两焦点,以线段F1F2为边作正三角形MF1F2,若边MF1的中点在双曲线上,则双曲线的离心率是_____
3. (2005天津)设双曲线以椭圆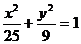 长轴的两个端点为焦点,其准线过椭圆的焦点,则双曲线的渐近线的斜率为 ( )
长轴的两个端点为焦点,其准线过椭圆的焦点,则双曲线的渐近线的斜率为 ( )
A.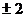 B.
B. C.
C.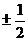 D.
D.
[填空题]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com