
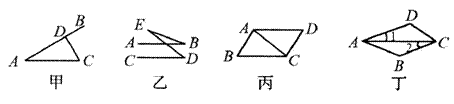
5.如图,结合图形作出了如下判断或推理:
①如图甲,CD⊥AB,D为垂足,那么点C到AB的距离等于C、D两点间的距离;
②如图乙,如果AB∥CD,那么∠B=∠D;
③如图丙,如果∠ACD=∠CAB,那么AD∥BC;
④如图丁,如果∠1=∠2,∠D=120°,那么∠BCD=60°.其中正确的个数是( )个.
 (A)1
(B)2 (C)3 (D)4
(A)1
(B)2 (C)3 (D)4
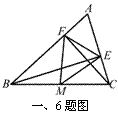
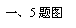
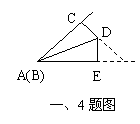
4.如图,将直角边AC=6cm,BC=8cm的直角△ABC纸片折叠,使点B与
点A重合,折痕为DE,则CD等于( )
(A)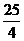 (B)
(B) 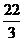 (C)
(C) 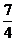 (D)
(D) 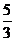
3. 将下列命题的条件与结论互换,得到的命题仍是真命题的是( ).
将下列命题的条件与结论互换,得到的命题仍是真命题的是( ).
(A)对顶角相等 (B)全等三角形的对应角相等
(C)直角三角形两锐角互余 (D)如果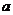 >
>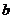 ,
,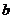 >
>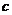 ,那么
,那么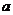 >
>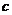
2. 已知线段
已知线段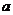 、
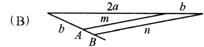
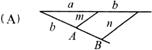
、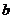 ,要想作一条线段AB,使AB=
,要想作一条线段AB,使AB=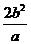 ,
,
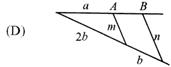
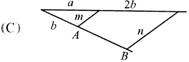
正确的作法是(图中直线m∥n)( ).
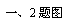
1.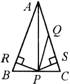 如图,已知△ABC中,AQ=PQ、PR=PS、PR⊥AB于R,PS⊥AC于S,
如图,已知△ABC中,AQ=PQ、PR=PS、PR⊥AB于R,PS⊥AC于S,
有以下三个结论:①AS=AR;②QP∥AR;③△BRP≌△CSP,其中( ).
(A)全部正确 (B)仅①正确 (C)仅①、②正确 (D)仅①、③正确
22. 解:(Ⅰ)设点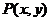 ,根据题意则有:
,根据题意则有:
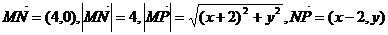
代入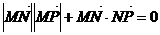 得:
得: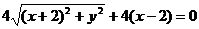 …………3分
…………3分
整理得点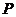 的轨迹
的轨迹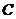 的方程
的方程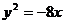 …………………………5分
…………………………5分
(Ⅱ)设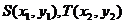 由题意得:
由题意得: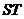 的方程为
的方程为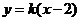 (显然
(显然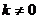 )
)
与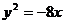 联立消元得:
联立消元得: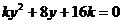 …………………………7分
…………………………7分
则有: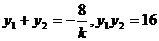
因为直线交轨迹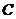 于两点,则
于两点,则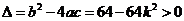 ,
,
再由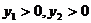 ,则
,则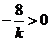 ,故
,故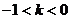 ………………………8分
………………………8分
可求得线段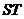 中点
中点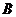 的坐标为
的坐标为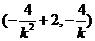
所以线段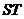 的垂直平分线方程为
的垂直平分线方程为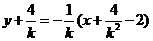 …………………………10分
…………………………10分
令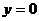 得点
得点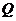 横坐标为
横坐标为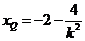 …………………………………12分
…………………………………12分
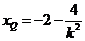
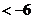
所以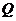 点横坐标的取值范围为
点横坐标的取值范围为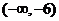 …………14分
…………14分
21.解:(Ⅰ)设切点坐标为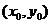 ,
, 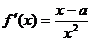 ………………………2分
………………………2分
则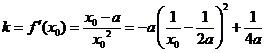 …………………………4分
…………………………4分
根据题意知: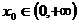 ,即
,即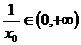 ,所以
,所以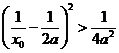
又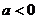 ,则
,则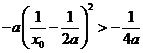 ,即
,即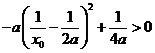
所以 …………………………6分
…………………………6分
(Ⅱ)显然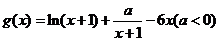 的定义域为
的定义域为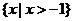 ………7分
………7分
则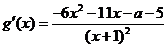 ………………………8分
………………………8分
又因为函数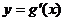 的图象经过点
的图象经过点 ,代入
,代入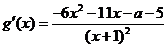
求得: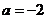 ,则
,则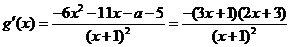 ……………10分
……………10分
由此可知:当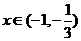 时,有
时,有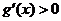 ,此时
,此时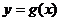 为单调增函数;
为单调增函数;
当 时,有
时,有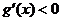 ,此时
,此时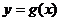 为单调减函数;
为单调减函数;
所以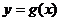 在区间
在区间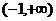 上只有极大值即
上只有极大值即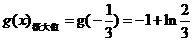 …12分
…12分
20.解:(Ⅰ) 由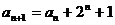 变形得:
变形得: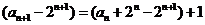
即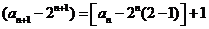
所以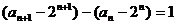 …………………4分
…………………4分
故数列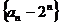 是以
是以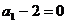 为首项,
为首项,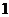 为公差的等差数列………………………5分
为公差的等差数列………………………5分
(Ⅱ)由(Ⅰ)得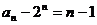 …………………………6分
…………………………6分
所以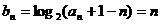 …………………………7分
…………………………7分
设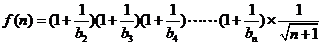 ………………8分
………………8分
则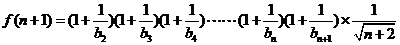
两式相除得: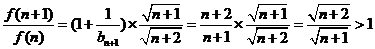 ……10分
……10分
所以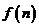 是关于
是关于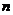 的单调递增函数,则
的单调递增函数,则
故实数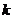 的取值范围是
的取值范围是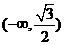 …………………………12分
…………………………12分
19.(Ⅰ)证明:因为 ,
,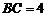 ,
,
所以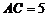 ,从而
,从而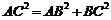 ,即
,即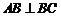 .………………2分
.………………2分
又因为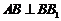 ,而
,而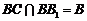 ,
,
所以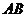
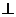 平面
平面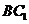 ,又
,又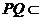 平面
平面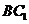
所以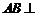
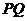 ;………………4分
;………………4分
(Ⅱ)解:过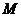 作
作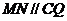 交
交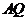 于
于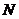 ,连接
,连接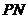 ,
,
因为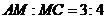
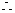
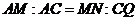
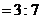 ……………6分
……………6分
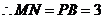
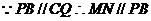
 四边形
四边形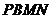 为平行四边形
为平行四边形
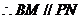 ,所以
,所以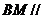 平面
平面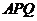 …………………………8分
…………………………8分
(III)解:由图1知,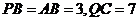 ,分别以
,分别以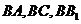 为
为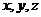 轴,
轴,
则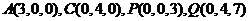


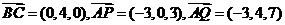 ………10分
………10分
设平面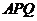 的法向量为
的法向量为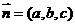 ,所以
,所以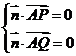 得
得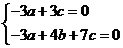 ,
,
令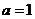 ,则
,则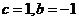 ,
,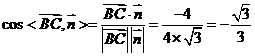
所以直线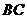 与平面
与平面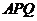 所成角的正弦值为
所成角的正弦值为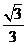 …………………………12分
…………………………12分
18. (本小题满分12分)
解:(Ⅰ)2袋食品都为废品的情况为
①2袋食品的三道工序都不合格 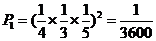 ……………2分
……………2分
②有一袋食品三道工序都不合格,另一袋有两道工序不合格
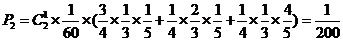 ……………4分
……………4分
③两袋都有两道工序不合格 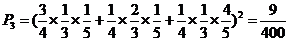
所以2袋食品都为废品的概率为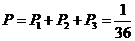 ……………6分
……………6分
(Ⅱ)
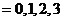
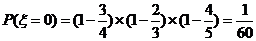
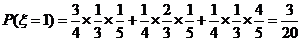 ………8分
………8分

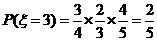 ………10分
………10分

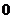
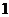
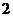
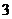
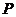
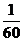
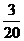
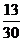
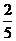
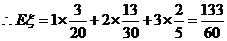 ………12分
………12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com