
5.(09·广东理科基础·10)关于地球的第一宇宙速度,下列表述正确的是 ( A )
A.第一宇宙速度又叫环绕速度
B.第一宇宙速度又叫脱离速度
C.第一宇宙速度跟地球的质量无关
D.第一宇宙速度跟地球的半径无关
解析:第一宇宙速度又叫环绕速度A对,B错;根据定义有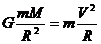
可知与地球的质量和半径有关,CD错。
4.(09·江苏物理· 3)英国《新科学家(New Scientist)》杂志评选出了2008年度世界8项科学之最,在XTEJ1650-500双星系统中发现的最小黑洞位列其中,若某黑洞的半径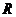 约45km,质量
约45km,质量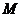 和半径
和半径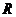 的关系满足
的关系满足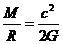 (其中
(其中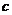 为光速,
为光速,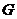 为引力常量),则该黑洞表面重力加速度的数量级为
( C )
为引力常量),则该黑洞表面重力加速度的数量级为
( C )
A.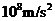 B.
B.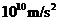
C.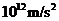 D.
D.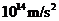
解析:处理本题要从所给的材料中,提炼出有用信息,构建好物理模型,选择合适的物理方法求解。黑洞实际为一天体,天体表面的物体受到的重力近似等于物体与该天体之间的万有引力,对黑洞表面的某一质量为m物体有: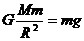 ,又有
,又有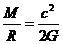 ,联立解得
,联立解得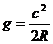 ,带入数据得重力加速度的数量级为
,带入数据得重力加速度的数量级为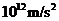 ,C项正确。
,C项正确。
3.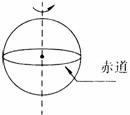 (09·广东物理·5)发射人造卫星是将卫星以一定的速度送入预定轨道。发射场一般选择在尽可能靠近赤道的地方,如图这样选址的优点是,在赤道附近
( B )
(09·广东物理·5)发射人造卫星是将卫星以一定的速度送入预定轨道。发射场一般选择在尽可能靠近赤道的地方,如图这样选址的优点是,在赤道附近
( B )
A.地球的引力较大
B.地球自转线速度较大
C.重力加速度较大
D.地球自转角速度较大
解析:由于发射卫星需要将卫星以一定的速度送入运动轨道,在靠进赤道处的地面上 的物体的线速度最大,发射时较节能,因此B正确。
2.(09·上海物理·8)牛顿以天体之间普遍存在着引力为依据,运用严密的逻辑推理,建立了万有引力定律。在创建万有引力定律的过程中,牛顿 ( AB )
A.接受了胡克等科学家关于“吸引力与两中心距离的平方成反比”的猜想
B.根据地球上一切物体都以相同加速度下落的事实,得出物体受地球的引力与其质量成正比,即Fµm的结论
C.根据Fµm和牛顿第三定律,分析了地月间的引力关系,进而得出Fµm1m2
D.根据大量实验数据得出了比例系数G的大小
解析:题干要求“在创建万有引力定律的过程中”,牛顿知识接受了平方反比猜想,和物体受地球的引力与其质量成正比,即Fµm的结论,而提出万有引力定律后,后来利用卡文迪许扭称测量出万有引力常量G的大小,只与C项也是在建立万有引力定律后才进行的探索,因此符合题意的只有AB。
1.(09·全国Ⅰ·19)天文学家新发现了太阳系外的一颗行星。这颗行星的体积是地球的4.7倍,是地球的25倍。已知某一近地卫星绕地球运动的周期约为1.4小时,引力常量G=6.67×10-11N·m2/kg2,,由此估算该行星的平均密度为 ( D )
A.1.8×103kg/m3 B. 5.6×103kg/m3
C. 1.1×104kg/m3 D.2.9×104kg/m3
解析:本题考查天体运动的知识.首先根据近地卫星饶地球运动的向心力由万有引力提供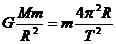 ,可求出地球的质量.然后根据
,可求出地球的质量.然后根据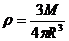 ,可得该行星的密度约为2.9×104kg/m3。
,可得该行星的密度约为2.9×104kg/m3。
2、人造天体的发射与变轨
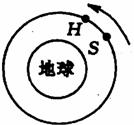 [例3]一组太空人乘坐大空穿梭机,去修理位于离地球表面 6.0×105m的圆形轨道上的哈勃太空望远镜H.机组人员使穿梭机S进入与H相同的轨道并关闭推动火箭,而望远镜则在穿梭机前方数公里处,如图所示,设G为引力常数,而ME为地球质量.(已知:地球半径为 6.4×106m)
[例3]一组太空人乘坐大空穿梭机,去修理位于离地球表面 6.0×105m的圆形轨道上的哈勃太空望远镜H.机组人员使穿梭机S进入与H相同的轨道并关闭推动火箭,而望远镜则在穿梭机前方数公里处,如图所示,设G为引力常数,而ME为地球质量.(已知:地球半径为 6.4×106m)
(1)在穿梭机内,一质量为70kg的太空人的视重是多少?
(2)①计算轨道上的重力加速度的值.
②计算穿梭机在轨道上的速率和周期.
(3)①证明穿梭机的总机械能跟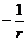 成正比,r为它的轨道半径.
成正比,r为它的轨道半径.
[注:若力 F与位移r之间有如下的关系:F=K/r2(其中K为常数),则当r由∞处变为0,F做功的大小可用以下规律进行计算: W= K/r(设∞处的势能为0)].
②穿梭机须首先螺旋进入半径较小的轨道,才有较大的角速度以超前望远镜.用上题的结果判所穿梭机要进入较低轨道时应增加还是减少其原有速率,解释你的答案.
[解析]:(1)在穿梭机内,一质量为70kg的太空人的视重为0.
(2)①因为mg/=G[MEm/(R+h)2],所以 g/=GME/(R+h)2,其中R=6.4×106m, h=6.0×105m.g/=8.2m/s2
②地球对穿梭机的万有引力提供向心力.
有:GMEm/(R+h)2=mv2/(R+h)=m(2π/T)2(R十h),
所以v=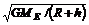 =7.6×103m/s
=7.6×103m/s
T=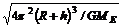 =5.8×103s.
=5.8×103s.
(3)①因为万有引力 F =GMEm/r2满足F=k(1/r2)(其中 k=GMEm为常数),由“注”可知,当穿梭机与地球之间的距离由∞处变到r时,万有引力对其所做的功w=k/r=GMEm/r,又因为:万有引力对穿梭机做多少功,其重力势能就减小多少,若设∞处的势能为零,则穿梭机在半径为r的轨道上时。其重力势能为E=一GMEm/r,则穿梭机此时的总机械能E总=EP十Ek=一GMEm/r十½mv2.代入(2)中的v值,得:
E总=一GMEm/r十½m(GME/r)=一(GMEm/2)(1/r)
故穿梭机的总机械能跟一1/r成正比,得证.
因为E总跟一1/r成正比,故进入低轨道时总机械能要减小,故必须减速,使总机械能减小,当速度减小后,在引力场的作用下进行低轨道运行,因引力做正功,动能增加,低轨道环绕速度vr/大于原轨道环绕速度vr,又因为v=ωr,vr/>vr,r/<r,则ωr/>ωr,从而获得较大的角速度,则可能赶上哈勃太空望远镜.
[例4] 如图所示,某次发射同步卫星时,先进入一个近地的圆轨道,然后在P点点火加速,进入椭圆形转移轨道(该椭圆轨道的近地点为近地圆轨道上的P,远地点为同步轨道上的Q),到达远地点时再次自动点火加速,进入同步轨道。设卫星在近地圆轨道上运行的速率为v1,在P点短时间加速后的速率为v2,沿转移轨道刚到达远地点Q时的速率为v3,在Q点短时间加速后进入同步轨道后的速率为v4。试比较v1、v2、v3、v4的大小,并用小于号将它们排列起来______。
 解析:根据题意有v2>v1、v4>v3,而v1、v4是绕地球做匀速圆周运动的人造卫星的线速度,由式②知v1>v4,故结论为v2>v1>v4>v3。卫星沿椭圆轨道由P→Q运行时,由机械能守恒可知,其重力势能逐渐增大,动能逐渐减小,因此有v2>v3。]
解析:根据题意有v2>v1、v4>v3,而v1、v4是绕地球做匀速圆周运动的人造卫星的线速度,由式②知v1>v4,故结论为v2>v1>v4>v3。卫星沿椭圆轨道由P→Q运行时,由机械能守恒可知,其重力势能逐渐增大,动能逐渐减小,因此有v2>v3。]
卫星的回收实际上是卫星发射过程的逆过程。
[例5]在空中飞行了十多年的“和平号”航天站已失去动力,由于受大气阻力作用其绕地球转动半径将逐渐减小,最后在大气层中坠毁,在此过程中下列说法正确的是( )
A.航天站的速度将加大 B.航天站绕地球旋转的周期加大
C.航天站的向心加速度加大 D.航天站的角速度将增大
[解析]由GMm/r2=mv2/r=mrω2=mr(2π/T)2=ma
得v=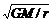 , ω=
, ω=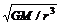 . T=2π
. T=2π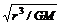
可知r减小,v增大,ω增大,T减小,a增大.A、C、 D正确.
[例6]“神舟三号”顺利发射升空后,在离地面340km的圆轨道上运行了108圈。运行中需要进行多次“轨道维持”。所谓“轨道维持”就是通过控制飞船上发动机的点火时间和推力的大小方向,使飞船能保持在预定轨道上稳定运行。如果不进行轨道维持,由于飞船受轨道上稀薄空气的摩擦阻力,轨道高度会逐渐降低,在这种情况下飞船的动能、重力势能和机械能变化情况将会是
A.动能、重力势能和机械能都逐渐减小
B.重力势能逐渐减小,动能逐渐增大,机械能不变
C.重力势能逐渐增大,动能逐渐减小,机械能不变
D.重力势能逐渐减小,动能逐渐增大,机械能逐渐减小
[由于阻力很小,轨道高度的变化很慢,卫星运行的每一圈仍可认为是匀速圆周运动。由于摩擦阻力做负功所以卫星的机械能减小;由于重力做正功所以重力势能减小;由式②可知卫星动能将增大(这也说明重力做的功大于克服阻力做的功,外力做的总功为正)。答案选D。]
[例7]飞船发射过程是一个加速过程,在加速过程中,宇航员处于__超重状态____状态。人们把这种状态下的重力与静止在地球表面时的重力的比值称为耐受力值,用K表示,则K=__ K=1+a/g _____(设宇航员的质量为m,加速上升加速度为a),选择宇般员时,要求他在此状态的耐受值为4≤K≤12,说明飞船发射时的加速度值的变化范围__3g≤a≤11g _______.
[例8]飞船在发射升空时,如果宇航员是站立的,则他的心血管系统受到何种影响?你认为宇航员采取什么资势为好?
答:由于在发射升空过程中,人处于超衙状态下,头部血压降低,足部血压升高,使大量血液淤积在下肢静脉中,严重影响静脉血的回流,使心脏输出血量不足,造成头部供血不足,轻则引起视觉障碍,重则可能导致意识丧失,所以宇航员采用平躺姿势为好。
[例9]航天飞船进入距地表3R地的轨道绕地球做圆周运动时,质量为64kg的宇航员处于_完全失重___状态,他的视重为__0___N。实际所受力__40___N。
[例10]若飞船要与轨道空间站对接,飞船为了追上轨道空间站( A )
A可以从较低的轨道上加速 B可以从较高的轨道上加速
C可以从与空间站同一轨道上加速 D无论在什么轨道上,只要加速都行
[例11] 我国的国土辽阔,在东西方向上分布在东经70°到东经135°的广大范围内,所以我国发射的同步通信卫星一般定点在赤道上空3.6万公里,东经100°附近。假设某颗通信卫星计划定点在赤道上空东经104°的位置。经测量刚进入轨道时它位于赤道上空3.6万公里,东经103°处。为了把它调整到104°处,可以短时间启动星上的小型发动机,通过适当调整卫星的轨道高度,改变其周期,从而使其自动“漂移”到预定经度。然后再短时间启动星上的小型发动机调整卫星的高度,实现最终定点。这两次调整高度的方向应该依次是
A.向下、向上 B.向上、向下 C.向上、向上 D.向下、向下
[东经103°在东经104°西边,为使卫星向东漂移,应使它的周期变小,为此应降低其高度,所以先向下;到达东经104°后,再向上。]
[例12]设想宇航员完成了对火星表面的科学考察任务,乘坐返回舱返回围绕火星做圆周运动的轨道舱,如图所示.为了安全,返回舱与轨道舱对接时,必须具有相同的速度.求该宇航员乘坐的返回舱至少需要获得多少能量,才能返回轨道舱?
已知:返回过程中需克服火星引力做功W=mgR(1一R/r),返回舱与人的总质量为m,火星表面重力加速度为g,火星半径为R,轨道舱到火星中心的距离为r;不计火星表面大气对返回舱的阻力和火星自转的影响.
 解析:物体m在火星M表面附近时,有
解析:物体m在火星M表面附近时,有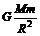 =mg解得GM=gR2
=mg解得GM=gR2
设轨道舱的质量为m0,速度大小为v,则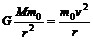
返回舱与轨道舱对接时,应具有的动能为Ek=½mv2
联立解得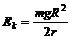
依题意知返回舱返回过程需克服引力做功W=mgR(1-R/r)
返回舱返回时至少需要能量为W总=Ek + W=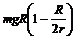
说明:这是一道关于天体运动的信息题.题中有多个对象,解题时要分清研究对象,选好规律.
[例13]2003年10月15日上午9时,我国在酒泉卫星发射中心成功发射“神舟五号”载人航天飞船,这是我国首次实现载人航天飞行,也是全世界第三个具有发射载人航天器能力的国家.“神舟五号”飞船长8. 86 m ;质量为7990 kg.飞船在达到预定的椭圆轨道后运行的轨道倾角为42. 4 0,近地点高度200 km,远地点高度约350 km.实行变轨后,进入离地约350 km的圆轨道上运行,飞船运动14圈后,于16日凌晨在内蒙古成功着陆.(地球半径Ro=-6.4×106 m,地球表面重力加速度g=10 m/s2,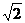 ·
·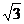 ·
·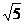 =5.48,计算结果保留三位有效数字)求:
=5.48,计算结果保留三位有效数字)求:
(1)飞船变轨后在轨道上正常运行时的速度.
(2)飞船在圆轨道上运行的周期.
解析:设飞船的质量为m,地球质量为M.飞船在圆轨道上运行时: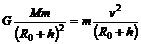
对于地面上质量为m0的物体有: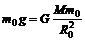
由上两式得飞船的运行速度为: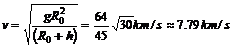
飞船在圆轨道上运行时的周期为:
 说明:天体运动的问题,要紧扣两条主线:万有引力提供向心力,重力等于万有引力.
说明:天体运动的问题,要紧扣两条主线:万有引力提供向心力,重力等于万有引力.
[补例]地球赤道上的N城市想实施一个“人造月亮”计划,在地球同步卫星上用一面平面镜将太阳光射到地球上,使这座城市在午夜时分有“日出”时的效果,若此时的N城市正值盛夏季节,地球的半径为R,自转周期为T,地球表面重力加速度为g,太阳在非常遥远的地方.求
(1)地球同步卫星离地心的距离
(2)悬挂平面镜的同步卫星所在经度平面的经度与N城的经度差α。
(3)此时平面镜与卫星所在经度平面的夹角θ
解析:(1)设地球及同步卫星的质量分别为M,m,则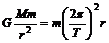
又:g=GM/R2,可得: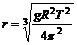
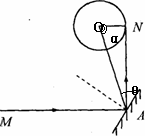
(2)过赤道平面的截面图如图所示,水平入射光线MA经反射后的反射光线AN与地球相切,故∠MAN=900
卫星所在经线在平面内的投影为OA,N城市所在经线在平面内的投影为ON,
所以:α=arccos ( R/r)
θ=450+arcsin(R/r)
说明:本题的关键是理解“午夜万分有‘日出’时的效果”的含义,并要有一定的空间想象力,且能画出截面图,能力要求较高.
试题展示
I.人造卫星做圆轨道和椭圆轨道运行的讨论
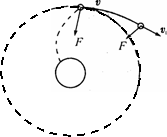 当火箭与卫星分离时,设卫星的速度为v(此即为发射速度),卫星距离地心为r,并设此时速度与万有引力垂直(通过地面控制可以实现)如图所示,则
当火箭与卫星分离时,设卫星的速度为v(此即为发射速度),卫星距离地心为r,并设此时速度与万有引力垂直(通过地面控制可以实现)如图所示,则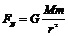 ,若卫星以v绕地球做圆周运动,则所需要的向心力为:F向=
,若卫星以v绕地球做圆周运动,则所需要的向心力为:F向=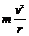
①当F万=F向时,卫星将做圆周运动.若此时刚好是离地面最近的轨道,则可求出此时的发射速度v=7.9 km/s.
②当F万<F向时,卫星将做离心运动,做椭圆运动,远离地球时引力做负功,卫星动能转化为引力势能.(神州五号即属于此种情况)
③当F万>F向时,卫星在引力作用下,向地心做椭圆运动,若此时发生在最近轨道,则v<7.9 km/s,卫星将坠人大气层烧毁。
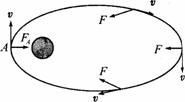 因此:星箭分离时的速度是决定卫星运行轨道的主要条件.
因此:星箭分离时的速度是决定卫星运行轨道的主要条件.
2.人造卫星如何变轨
卫星从椭圆轨道变到圆轨道或从圆轨道变到椭圆轨道是卫星技术的一个重要方面,卫星定轨和返回都要用到这个技术.
以卫星从椭圆远点变到圆轨道为例加以分析:如图所示,在轨道A点,万有引力FA>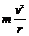 ,要使卫星改做圆周运动,必须满足FA=
,要使卫星改做圆周运动,必须满足FA=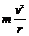 和FA⊥v,在远点已满足了FA⊥v的条件,所以只需增大速度,让速度增大到
和FA⊥v,在远点已满足了FA⊥v的条件,所以只需增大速度,让速度增大到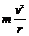 =FA,这个任务由卫星自带的推进器完成.
=FA,这个任务由卫星自带的推进器完成.
这说明人造卫星要从椭圆轨道变到大圆轨道,只要在椭圆轨道的远点由推进器加速,当速度达到沿圆轨道所需的速度,人造卫星就不再沿椭圆轨道运动而转到大圆轨道.“神州五号”就是通过这种技术变轨的,地球同步卫星也是通过这种技术定点于同步轨道上的.
规律方法1、处理人造天体问题的基本思路
由于运行中的人造天体,万有引力全部提供人造地球卫星绕地球做圆周运动的向心力,因此所有的人造地球卫星的轨道圆心都在地心.解关于人造卫星问题的基本思路:①视为匀速圆周运动处理;②万有引力充当向心力;③根据已知条件选择向心加速度的表达式便于计算;④利用代换式gR2=GM推导化简运算过程。
注意:①人造卫星的轨道半径与它的高度不同.②离地面不同高度,重力加速度不同,
[例l]设人造地球卫星绕地球做匀速圆周运动,卫星离地面越高,则卫星的( )
A.速度越大 B.角速度越大 C.向心加速度越大;D.周期越长
解析:(1)v与 r的关系: G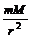 = m
= m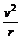 ;
;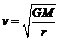 即
即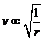 (r越大v越小).所以答案A错误.(2)ω与r的关系:G
(r越大v越小).所以答案A错误.(2)ω与r的关系:G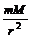 =mω2r ,
=mω2r ,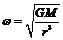 ,即
,即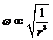 (r越大,ω越小).所以答案B错误.(3)a与r的关系:G
(r越大,ω越小).所以答案B错误.(3)a与r的关系:G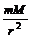 =ma,a=GM/r2,即a∝1/r2。卫星绕轨道半径 r运转时的向心加速度与该处的重力加速度g/相等,所以 g/=a, g/∝1/r2,(r越大.加速度越小).所以答案C错误.(4)T与r的关系:G
=ma,a=GM/r2,即a∝1/r2。卫星绕轨道半径 r运转时的向心加速度与该处的重力加速度g/相等,所以 g/=a, g/∝1/r2,(r越大.加速度越小).所以答案C错误.(4)T与r的关系:G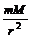 =m
=m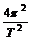 r ,T=2π
r ,T=2π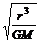 即T∝
即T∝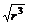 ( r越大,T越大).所以答案D正确.
( r越大,T越大).所以答案D正确.
因 GM=g0R02,所以 T=2π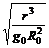 ,当 r=Ro时,T=Tmin=2π
,当 r=Ro时,T=Tmin=2π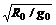 答案:D
答案:D
说明:可以看出,绕地球做匀速圆周运动的人造卫星的轨道半径r、线速度大小v和周期T是一一对应的,其中一个量确定后,另外两个量也就唯一确定了。离地面越高的人造卫星,线速度越小而周期越大。
[例2]设地球的半径为R0,质量为m的卫星在距地面R0高处做匀速圆周运动,地面的重力加速度为g0,则以下说法错误的是( )
A.卫星的线速度为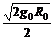 ; B.卫星的角速度为
; B.卫星的角速度为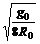 ;
;
C.卫星的加速度为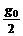 ;
D.卫星的周期
;
D.卫星的周期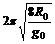 ;
;
解析:在地面: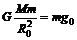 ;在高空:
;在高空: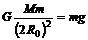 ;
;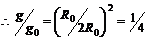
g=¼g0;此重力加速度即为卫星的向心加速度故C选项错误.
卫星的线速度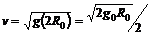 故A选项正确.
故A选项正确.
周期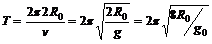 故D选项正确
故D选项正确
角速度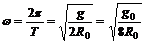 故B选项正确
故B选项正确
当人造天体具有较大的动能时,它将上升到较高的轨道运动,而在较高轨道上运动的人造天体却具有较小的动能。反之,如果人造天体在运动中动能减小,它的轨道半径将减小,在这一过程中,因引力对其做正功,故导致其动能将增大。
同样质量的卫星在不同高度轨道上的机械能不同。其中卫星的动能为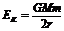 ,由于重力加速度g随高度增大而减小,所以重力势能不能再用Ek=mgh计算,而要用到公式
,由于重力加速度g随高度增大而减小,所以重力势能不能再用Ek=mgh计算,而要用到公式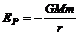 (以无穷远处引力势能为零,M为地球质量,m为卫星质量,r为卫星轨道半径。由于从无穷远向地球移动过程中万有引力做正功,所以系统势能减小,为负。)因此机械能为
(以无穷远处引力势能为零,M为地球质量,m为卫星质量,r为卫星轨道半径。由于从无穷远向地球移动过程中万有引力做正功,所以系统势能减小,为负。)因此机械能为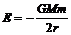 。同样质量的卫星,轨道半径越大,即离地面越高,卫星具有的机械能越大,发射越困难。
。同样质量的卫星,轨道半径越大,即离地面越高,卫星具有的机械能越大,发射越困难。
(1)卫星进入轨道前加速过程,卫星上物体超重.
(2)卫星进入轨道后正常运转时,卫星上物体完全失重.
卫星飞行速度及周期仅由距地高度决定与质量无关。
设卫星距地面高度为h,地球半径为R,地球质量为M,卫星飞行速度为v,则由万有引力充当向心力可得v=[GM/(R+h)]½。知道了卫星距离地面的高度,就可确定卫星飞行时的速度大小。
不同高度处人造地球卫星的环绕速度及周期见下表:
|
高度(km) |
0 |
300 |
500 |
1000 |
3000 |
5000 |
35900(同步轨道) |
38000(月球轨道) |
|
环绕速度(km/s) |
7.91 |
7 .73 |
7. 62 |
7.36 |
6.53 |
5.29 |
2.77 |
0.97 |
|
周期(分) |
84.4 |
90 .5 |
94.5 |
105 |
150 |
210 |
23小时56分 |
28天 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com