5.(cos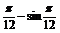)(cos)=　　　　　　　 .

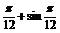答案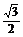　

4.已知cos2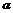=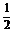(其中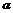∈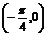)，则sin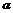的值为　　　　　 .

答案　 -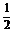

3.已知x∈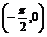,cos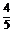x=,则tan2x=　　　　 .

答案　 -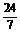

2.sin163°·sin223°+sin253°·sin313°=　　　　　 .

答案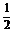　

1.已知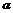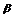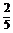tan(+)=,tan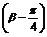=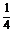,那么tan =　　　　　　 .

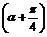答案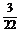　

3．嫦娥一号卫星于2007年10月24日在西昌卫星发射中心发射，在经历了长达494天的飞行后成功“受控撞月”。嫦娥一号首先经过变轨，由200 km圆轨道降到100 km圆轨道，通过减速、下落，最后最终大约以v=1.68 km/s的速度撞击到在月球的丰富海区域。

已知地球半径R₁=6.4×10⁶m；地球表面的重力加速度g=10m/s²，月球的质量约为地球质量的1/81，月球的半径约为地球半径的3/11，嫦娥一号的质量约为m=1.15×10³kg，在距离月球表面100 km的范围内，重力加速度约等于月球表面的重力加速度。 (计算结果保留2位有效数字)

　 (1)求月球表面的重力加速度；(保留2位有效数字)

　 (2)设嫦娥一号垂直撞击月球表面，与月球表面的作用时间t=0.10s，求撞击过程对月球的平均作用力大小；

　 (3)在嫦娥一号从h=100km圆轨道到撞击月球的过程中，飞船发动机所做的功。

2．如图17所示，将质量M=1.20 kg的小沙箱，用轻质软绳(不可伸长)悬挂起来，开始处于静止状态，绳的长度l=0.80 m。用枪向沙箱发射质量m=0.05 kg的子弹，子弹以v₀=100 m/s 的速度向右水平击中小沙箱，并留在小砂箱中，小沙箱沿竖直面向上摆动。假设沙箱每次向左运动到最低点时就恰好有两颗同样速度的子弹先后射入沙箱并留在沙箱中，子弹射入沙箱的过程时间极短，可忽略不计，重力加速度g取10 m/s²，不计空气阻力。求：

　 (1)第一颗子弹射入沙箱的过程中子弹对砂箱的冲量大小；

　 (2)第一颗子弹射入沙箱并相对沙箱静止的瞬间，砂箱对绳的拉力的大小；

　 (3)第一颗子弹射入沙箱后，砂箱摆动的最大高度；

　 (4)要使沙箱摆动的最大角度小于60°，射入沙箱的子弹数目至少为多少？

1．游乐场内有一种叫“空中飞椅”的游乐项目，示意图如图16所示，在半径为r=4m的水平转盘的边缘固定着N=10条长为L=10m的钢绳，纲绳的另一端连接着座椅(图中只画出2个)，转盘在电动机带动下可绕穿过其中心的竖直轴OO′转动。设在每个座椅内坐着质量相同的人，可将人和座椅看成是一个质点，人和座椅的质量为m=60kg，已知重力加速度为g=10m/s²，不计钢绳的重力及空气的阻力。当转盘以某一角速度w匀速转动时，座椅从静止开始随着转盘的转动而升高，经过一段时间后达到稳定状态，此时钢绳与转轴在同一竖直平面内，与竖直方向的夹角为θ=37°。求

　 (1)稳定时钢绳对座椅的拉力F的大小及转盘转动的角速度ω；

　 (2)每个座椅从静止开始到随转盘稳定转动的过程中，绳子的拉力对座椅做的功；

　 (3)如果带动转盘的电动机输出机械功率的效率为80%，转盘因自身转动及克服各种摩擦损失的机械功率为20%，求从座椅开始运动到随转盘稳定转动的过程中，电动机消耗的电能。

3．验证碰撞中的动量守恒

为了验证碰撞中的动量守恒和检验两个小球的碰撞是否为弹性碰撞(碰撞过程中没有机械能损失)，某同学选取了两个体积相同、质量不等的小球，按下述步骤作了如下实验：

①用天平测出两个小球的质量分别为m₁和m₂，且m₁>m₂。

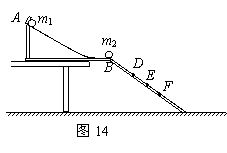②按照如图14所示的那样，安装好实验装置。将斜槽AB固定在桌边，使槽的末端点的切线水平，将一斜面BC连接在斜槽末端。

③先不放小球m₂，让小球m₁从斜槽顶端A处由静止滚下， 记下小球m₁在斜面上的落点位置。

④将小球m₂放在斜槽前端边缘处，让小球m₁从斜槽顶端A处由静止滚下，使它们发生碰撞，记下小球m₁和 m₂在斜面上的落点位置。

⑤用毫米刻度尺量出各个落点位置到斜槽末端点B的距离。图中D、E、F点是该同学记下的小球在斜面上的几个落点位置，到B点的距离分别为L_D、L_E、L_F。

根据该同学的实验，回答下列问题：

　 (1)小球m₁与m₂发生碰撞后，m₁的落点是图中的D点，m₂的落点是图中的 F点。

　 (2)用测得的物理量来表示，只要满足关系式m₁=m₁+ m₂，则说明碰撞中动量是守恒的。

　 (3)用测得的物理量来表示，只要再满足关系式m₁ L_E =m₁L_D+ m₂ L_F，则说明两小球的碰撞是弹性碰撞。

分析：设小球水平速度为v时，经历时间t达到斜面上，水平位移为x，竖直位移为y，沿斜面位移为s，则x=vt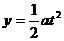，，y/x=tanα，s=x/cosα，由以上各式得。

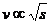计算题

2．用油膜法估测油酸分子直径的大小。

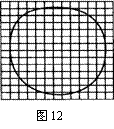　 (1)在“用油膜法估测分子大小”实验中所用的油酸酒精溶液的浓度为 1000 mL溶液中有纯油酸O.6mL，用注射器测得1mL上述溶液为80滴，把1滴该溶液滴入盛水的浅盘内，让油膜在水面上尽可能散开，测得油酸薄膜的轮廓形状和尺寸如图12所示，图中正方形方格的边长为1cm，试求：

　 (1)油酸膜的面积是113cm²；

　 (2)实验测出油酸分子的直径是6.6×10^-10m；(结果保留两位

有效数字)

　 (3)实验中为什么要让油膜尽可能散开?

答：形成单分子油膜。

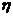　 (2)①现将1滴配置好的浓度=1/700的油酸水溶液滴入盛水的浅盘中，让油膜在水面上尽可能散开，待液面稳定后，在水面上形成油酸的单分子油膜；

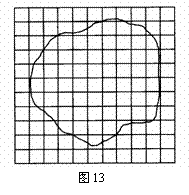
②把带有方格的玻璃板放在浅盘上，在玻璃板上描绘出油膜的边界轮廓，形状如图13所示。已知坐标方格边长为L＝3.0cm，按要求数出油膜轮廓线包括的方格是n＝60个，则油酸的面积约为0.054m²；

③测得v₀=1.0毫升油酸溶液能滴出k＝75滴油酸溶液，由以上数据估测油酸分子直径的计算式为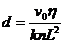(用v₀、n、k、L表示)。测得油酸分子直径约为4×10^-10m。(保留一位有效数字)