
1. 如图1所示,质量为m的物体静止于倾角为α的斜面体上,现对斜面体施
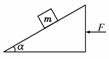
如图1所示,质量为m的物体静止于倾角为α的斜面体上,现对斜面体施
加一水平向左的推力F,使物体随斜面体一起沿水平面向左匀速移动x,
则在此匀速运动过程中斜面体对物体所做的功为 ( )
A.Fx B.mgxcosαsinα 图1
C.mgxsinα D.0
解析:由于物体做匀速运动,其处于平衡状态.物体动能和势能在运动过程中都不发生变化,故根据动能定理知合外力对物体做功为零.而重力做功为零,所以斜面体对物体做功为零,故应选D.
答案:D
12.已知椭圆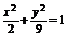 上任意一点P,由P向x轴作垂线段PQ,垂足为Q,点M在线段PQ上,且
上任意一点P,由P向x轴作垂线段PQ,垂足为Q,点M在线段PQ上,且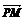 =2
=2 ,点M的轨迹为曲线E.
,点M的轨迹为曲线E.
(1)求曲线E的方程;
(2)若过定点F(0,2)的直线l交曲线E于不同的两点G,H(点G在点F,H之间),且满足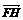 =2
=2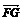 ,求直线l的方程.
,求直线l的方程.
解 (1)设M(x,y),P(x0,y0),
∵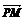 =2
=2 ,∴
,∴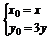 ,
,
将其代入椭圆方程得
得曲线E的方程为: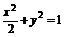 .
.
(2)设G(x1,y1)、H(x2,y2),
∵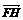 =2
=2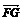 ,∴x2=2x1. ①
,∴x2=2x1. ①
依题意,当直线l斜率不存在时,G(0,1),H(0,-1),不满足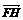 =2
=2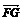 .故设直线l:y=kx+2,代入曲线E的方程并整理得(1+2k2)x2+8kx+6=0,
.故设直线l:y=kx+2,代入曲线E的方程并整理得(1+2k2)x2+8kx+6=0,
∴x1+x2=-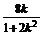 ,x1·x2=
,x1·x2=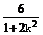 ②
②
联立①②解得k=±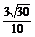 ,
,
所以直线l的方程为:y=±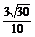 x+2.
x+2.
11.已知两条直线l1:2x-3y+2=0和l2:3x-2y+3=0,有一动圆(圆心和半径都动)与l1、l2都相交,且l1、l2被圆截得的弦长分别是定值26和24,求圆心的轨迹方程.
解 设动圆的圆心为M(x,y),半径为r,点M到直线l1,l2的距离分别为d1和d2.
由弦心距、半径、半弦长间的关系得,
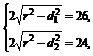 即
即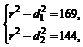
消去r得动点M满足的几何关系为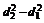 =25,
=25,
即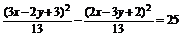 .
.
化简得(x+1)2-y2=65.
此即为所求的动圆圆心M的轨迹方程.
10.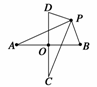 如图所示,线段AB与CD互相垂直平分于点O,|AB|=2a(a>0),|CD|=2b (b﹥0),动点P满足|PA|·|PB|=|PC|·|PD|.求动点P的轨迹方程.
如图所示,线段AB与CD互相垂直平分于点O,|AB|=2a(a>0),|CD|=2b (b﹥0),动点P满足|PA|·|PB|=|PC|·|PD|.求动点P的轨迹方程.
解 以O为坐标原点,直线AB、CD分别为x轴、y轴建立直角坐标系,
则A(-a,0),B(a,0),C(0,-b),D(0,b),
设P(x,y),由题意知
|PA|·|PB|=|PC|·|PD|,
∴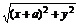 ·
·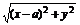
=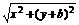 ·
·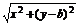 ,
,
化简得x2-y2=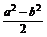 .
.
故动点P的轨迹方程为x2-y2=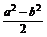 .
.
9.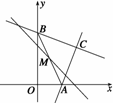 如图所示,已知点C的坐标是(2,2),过点C的直线CA与x轴交于点A,过点C且与直线CA垂直的直线CB与y轴交于点B.设点M是线段AB的中点,求点M的轨迹方程.
如图所示,已知点C的坐标是(2,2),过点C的直线CA与x轴交于点A,过点C且与直线CA垂直的直线CB与y轴交于点B.设点M是线段AB的中点,求点M的轨迹方程.
解 方法一 (参数法):设M的坐标为(x,y).
若直线CA与x轴垂直,则可得到M的坐标为(1,1).
若直线CA不与x轴垂直,设直线CA的斜率为k,则直线CB的斜率为- ,故直线CA方程为:y=k(x-2)+2,
,故直线CA方程为:y=k(x-2)+2,
令y=0得x=2-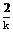 ,则A点坐标为(2-
,则A点坐标为(2-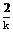 ,0).
,0).
CB的方程为:y=- (x-2)+2,令x=0,得y=2+
(x-2)+2,令x=0,得y=2+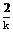 ,
,
则B点坐标为(0,2+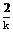 ),由中点坐标公式得M点的坐标为
),由中点坐标公式得M点的坐标为
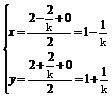 ①
①
消去参数k得到x+y-2=0 (x≠1),
点M(1,1)在直线x+y-2=0上,
综上所述,所求轨迹方程为x+y-2=0.
方法二 (直接法)设M(x,y),依题意A点坐标为(2x,0),B点坐标为(0,2y).∵|MA|=|MC|,
∴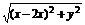 =
=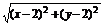 ,
,
化简得x+y-2=0.
方法三 (定义法)依题意|MA|=|MC|=|MO|,
即:|MC|=|MO|,所以动点M是线段OC的中垂线,故由点斜式方程得到:x+y-2=0.
8.平面上有三点A(-2,y),B(0,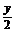 ),C(x,y),若
),C(x,y),若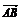 ⊥
⊥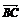 ,则动点C的轨迹方程为
.
,则动点C的轨迹方程为
.
答案 y2=8x
7.已知△ABC的顶点B(0,0),C(5,0),AB边上的中线长|CD|=3,则顶点A的轨迹方程为 .
答案 (x-10)2+y2=36(y≠0)
6.一圆形纸片的圆心为O,点Q是圆内异于O的一个定点,点A是圆周上一动点,把纸片折叠使点A与点Q重合,然后抹平纸片,折痕CD与OA交于点P,当点A运动时,点P的轨迹为 (写出形状即可).
答案 椭圆
5.F1、F2是椭圆的两个焦点,M是椭圆上任一点,从任一焦点向△F1MF2顶点M的外角平分线引垂线,垂足为P,则P点的轨迹为 (写出形状即可).
答案 圆
4.平面直角坐标系中,已知两点A(3,1),B(-1,3),若点C满足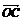 =
=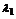
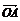 +
+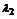
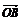 (O为原点),其中
(O为原点),其中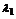 ,
,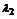 ∈R,且
∈R,且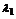 +
+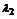 =1,则点C的轨迹是
(写出形状即可).
=1,则点C的轨迹是
(写出形状即可).
答案 直线
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com