9．(2009·北京市东城区质检)函数y＝log(x²－3x)的单调递减区间是________．

答案：(3，+∞)

解析：函数t＝x²－3x(t>0)的单调递增区间是(3，+∞)，由复合函数的单调性判断法则，函数y＝log(x²－3x)的单调递减区间是(3，+∞)．

8．已知f(x)＝是R上的增函数，那么a的取值范围是(　)

A．(1，+∞)　 　　　　　　　　　　　　　　　　　　　　　　　 B．(1，]

C．(1,2)　 　　　　　　　　　　　　　　　　　　　　　　　　　　　 D．[，2)

答案：D

解析：依题意得

解得a的取值范围是≤a<2，故选D.

7．(2008·重庆一模)设f(x)是定义在R上以2为周期的偶函数，已知x∈(0,1)时，f(x)＝log(1－x)，则函数f(x)在(1,2)上(　)

A．是增函数，且f(x)<0　 　　　　　　　　　　　　　　　 B．是增函数，且f(x)>0

C．是减函数，且f(x)<0　 　　　　　　　　　　　　　　　 D．是减函数，且f(x)>0

答案：D

解析：f(x)是定义在R上以2为周期的偶函数，由x∈(0,1)时，f(x)＝log(1－x)为增函数且f(x)>0得函数f(x)在(2,3)上也为增函数且f(x)>0，而直线x＝2为函数的对称轴，则函数f(x)在(1,2)上是减函数，且f(x)>0，故选D.

6．若函数f(x)是定义在R上的偶函数，在(－∞，0]上是减函数，且f(2)＝0，则使得f(x)<0的x的取值范围是(　)

A．(－∞，2)　 　　　　　　　　　　　　　　　　　　　　　　　 B．(2，+∞)

C．(－∞，－2)∪(2，+∞)　 　　　　　　　　　　　　 D．(－2,2)

答案：D

解析：∵f(2)＝0且f(x)为偶函数，∴f(－2)＝0.

又∵f(x)在(－∞，0]上递减，

∴f(x)在(－2,0]上递减．

∴对于x∈(－2,0]必有f(x)<0.

由对称性得对于x∈[0,2)必有f(x)<0.

∴使得f(x)<0的范围是(－2,2)．故选D.

5．若函数y＝log₂(x²－ax+3a)在[2，+∞)是增函数，则实数a的范围为(　)

A．(－∞，4]

B．(－4,4]

C．(－∞，－4)∪[2，+∞)

D．(－4,2)

答案：B

解析：本题考查含参数变量的函数的讨论及其复合函数的应用．由题知：y＝log₂x为单调增函数，y＝log₂(x²－ax+3a)的单调增区间为y＝x²－ax+3a的增区间的一个子区间，由y＝x²－ax+3a⇒y′＝2x－a，又在[2，+∞)是单调增区间，即在x∈[2，+∞),2x－a＞0恒成立，即只需2×2－a＞0即可⇒a＜4，又y＝x²－ax+3a在x∈[2，+∞)上恒大于0，则2²－2a+3a＞0⇒a＞－4，综上可得：－4＜a＜4，当a＝4时同样成立．故选B.

4．(2008·天津六区联考)设f(x)是定义在R上的单调递减的奇函数，若x₁+x₂>0，x₂+x₃>0，x₃+x₁>0，则(　)

A．f(x₁)+f(x₂)+f(x₃)>0

B．f(x₁)+f(x₂)+f(x₃)<0

C．f(x₁)+f(x₂)+f(x₃)＝0

D．f(x₁)+f(x₂)>f(x₃)

答案：B

解析：∵x₁+x₂>0，x₂+x₃>0，x₃+x₁>0，

∴x₁>－x₂，x₂>－x₃，x₃>－x₁.

又f(x)是定义在R上的单调递减的奇函数，

∴f(x₁)<－f(x₂)，f(x₂)<－f(x₃)，

f(x₃)<－f(x₁)，

∴f(x₁)+f(x₂)+f(x₃)<－[f(x₁)+f(x₂)+f(x₃)]，

∴f(x₁)+f(x₂)+f(x₃)<0，故选B.

3．(2008·广东六校联考)函数y＝log_a|x+2|在(－2,0)上是单调递增的，则此函数在(－∞，－2)上是(　)

A．单调递增　 　　　　　　　　　　　　　　　　　　　　　　　　 B．单调递减

C．先增后减　 　　　　　　　　　　　　　　　　　　　　　　　　 D．先减后增

答案：B

解析：函数y＝log_a|x+2|的对称轴为x＝－2，它在(－2,0)上是单调递增的，则此函数在(－∞，－2)上是单调递减的，故选B.

2．(2008·启东中学)若函数f(x)＝log_a(2x²+x)(a>0，a≠1)在区间内恒有f(x)>0，则f(x)的单调增区间是(　)

A.　　　　　　　　　　　　　　　　　　 B.

C.　 　　　　　　　　　　　　　　　　　　　　　　　 D．(0，+∞)

答案：C

解析：当x∈时，2x²+x∈(0,1)，则0<a<1，f(x)＝log_a(2x²+x)(a>0，a≠1)＝log_a，则f(x)的单调递增区间是，故选C.

1．(2008·北京海淀)下列函数中，在其定义域内既是奇函数又是增函数的是(　)

A．y＝－log₂x(x>0)

B．y＝x³+x(x∈R)

C．y＝3^x(x∈R)

D．y＝－(x∈R，x≠0)

答案：B

解析：奇函数只有y＝x³+x(x∈R)和y＝－(x∈R，x≠0)，但前者在定义域内是增函数，后者不是，故选B.

5.

I(1)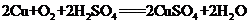(2分)；形成了原电池，加热蒸发、冷却结晶、过滤并洗涤晶体。

(2)丙，戊，乙，甲

Ⅱ(1)吸收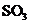放出等物质的量的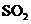

(2)干燥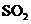和

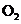
(3)②调节量筒使其液面与E装置中的液面持平。

　　 ③读曲量筒中液体体积时，视线与液体的凹液面相平。(其他合理答案均可)

(4)(2分，期于每空1分)