3．物理模型等效

物理模型等效在物理学习中应用十分广泛，特别是力学中的很多模型可以直接应用到电磁学中去，如卫星模型、人船模型、子弹射木块模型、碰撞模型、弹簧振子模型等．实际上，我们在学习新知识时，经常将新的问题与熟知的物理模型进行等效处理．

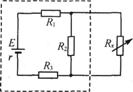例4．如图所示，R₁、R₂、R₃为定值电阻，但阻值未知，R_x为电阻箱．当R_x为R_x1=10 Ω时，通过它的电流I_x1=l A；当R_x为R_x2=18 Ω时，通过它的电流I_x2=0.6A．则当I_x3=0.l A时，求电阻R_x3．

例5．如图所示，倾角为θ=30⁰，宽度L=1 m的足够长的U形平行光滑金属导轨固定在磁感应强度B=1 T、范围足够大的匀强磁场中，磁场方向垂直导轨平面斜向上，用平行于导轨且功率恒为6 w的牵引力牵引一根质量m=0.2 kg，电阻R=1 Ω放在导轨上的金属棒ab由静止沿导轨向上移动，当金属棒ab移动2.8 m时获得稳定速度，在此过程中金属棒产生的热量为5.8 J(不计导轨电阻及一切摩擦，g取10 m／s²)，求：

　　 (1)金属棒达到的稳定速度是多大?

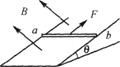　　 (2)金属棒从静止达到稳定速度所需时间是多少?

2．物理过程等效

　　 对于有些复杂的物理过程，我们可以用一种或几种简单的物理过程来替代，这样能够简化、转换、分解复杂问题，能够更加明确研究对象的物理本质，以利于问题的顺利解决．

　　 高中物理中我们经常遇到此类问题，如运动学中的逆向思维、电荷在电场和磁场中的匀速圆周运动、平均值和有效值等．

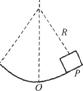
例2．如图所示，在竖直平面内，放置一个半径R很大的圆形光滑轨道，0为其最低点．在0点附近P处放一质量为m的滑块，求由静止开始滑至0点时所需的最短时间．

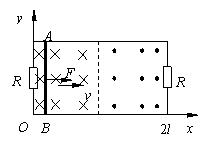
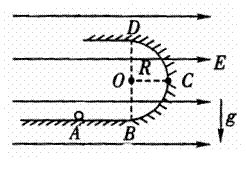
　 例3．矩形裸导线框长边的长度为2l，短边的长度为l，在两个短边上均接有阻值为R的电阻，其余部分电阻均不计．导线框的位置如图所示，线框内的磁场方向及分布情况如图，大小为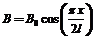．一电阻为R的光滑导体棒AB与短边平行且与长边始终接触良好．起初导体棒处于x=0处，从t=0时刻起，导体棒AB在沿x方向的外力F的作用下做速度为v的匀速运动.试求：

(1)导体棒AB从x=0运动到x=2l的过程中外力F随时间t变化的规律；

(2)导体棒AB从x=0运动到x=2l的过程中整个回路产生的热量．

1．物理量等效

　　 在高中物理中，小到等效劲度系数、合力与分力、合速度与分速度、总电阻与分电阻等；大到等效势能、等效场、矢量的合成与分解等，都涉及到物理量的等效．如果能将物理量等效观点应用到具体问题中去，可以使我们对物理问题的分析和解答变得更为简捷．

例l．如图所示，ABCD为表示竖立放在场强为E=10⁴V/m的水平匀强电场中的绝缘光滑轨道，其中轨道的BCD部分是半径为R的半圆环，轨道的水平部分与半圆环相切A为水平轨道的一点，而且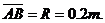把一质量m=100g、带电q=10^－4C的小球，放在水平轨道的A点上面由静止开始被释放后，在轨道的内侧运动。(g=10m/s²)求：

　 (1)它到达C点时的速度是多大？

　 (2)它到达C点时对轨道压力是多大？

　 (3)小球所能获得的最大动能是多少？

　　 等效法是科学研究中常用的思维方法之一，它是从事物的等同效果这一基本点出发的，它可以把复杂的物理现象、物理过程转化为较为简单的物理现象、物理过程来进行研究和处理，其目的是通过转换思维活动的作用对象来降低思维活动的难度，它也是物理学研究的一种重要方法．

　　 用等效法研究问题时，并非指事物的各个方面效果都相同，而是强调某一方面的效果．因此一定要明确不同事物在什么条件、什么范围、什么方面等效．在中学物理中，我们通常可以把所遇到的等效分为：物理量等效、物理过程等效、物理模型等效等．

6. 有一带负电的小球，其带电量q= -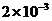C。如图所示，开始时静止在场强E=200N/C的匀强电场中的P点，靠近电场极板B有一挡板要S，小球与挡板S的距离h=5cm，与A板距离H=45cm，重力作用不计。在电场力作用下小球向左运动，与挡板S相碰后电量减少到碰前的k倍，已知k=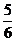，而碰后小球的速度大小不变。

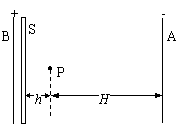(1)设匀强电场中挡板S所在位置的电势为零，则电场中P点的电势为多少？小球在P点时的电势能为多少？(电势能用E来表示)

(2)小球从P点出发第一次回到最右端的过程中电场力对小球做了多少功？

(3)小球经过多少次碰撞后，才能抵达A板？(取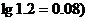

例题解析：

例1．解析 小球从h₀高处落地时，速率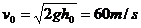

第一次跳起时和又落地时的速率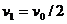

第二次跳起时和又落地时的速率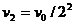

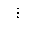
第m次跳起时和又落地时的速率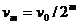

每次跳起的高度依次，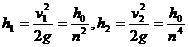

通过的总路程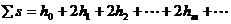

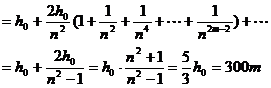
经过的总时间为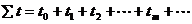

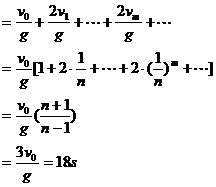
例2．(1)木板最初做匀速运动，由F＝μMg解得，　　　　

第l 块铁块放上后，木板做匀减速运动，加速度大小为a₁,即有：

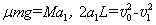
代人数据解得： 　　

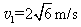
(2)设最终有n块铁块能静止在木板上．则木板运动的加速度大小为： 　 　　

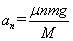
第1 块铁块放上后：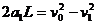

第2 块铁抉放上后：

第n块铁块放上后：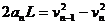

由上可得：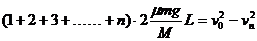　

木板停下时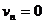，，得n=6.6．即最终有7 块铁块放在木板上．　　　

(3)从放上第1块铁块至刚放上第7 块铁块的过程中，由(2)中表达式可得：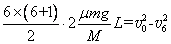　　

从放上第7 块铁块至木板停止运动的过程中，设木板发生的位移为d ，则：

联立解得：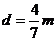　 　　　　

例3．(1)对A由动能定理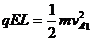：　　 (1)

解得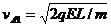；A与B相碰后速度交换。

故第一次相碰后，A速度为零；B速度为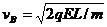　 (2)

(2)从A开始运动到碰第一次历时t₁=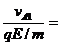

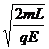
设第二次碰前A速为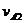 ，从第一次碰后到第二次碰前历时t₂

对A、由动能定理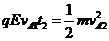：　　　 (3)　　

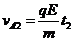　 (4)　　 (2分)由(3)、(4)两式得：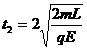

故两球第二次碰时经历的时间为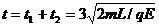：　 (5)　

(3)由(3)(4)两式解得：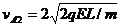

　　 此时B的速度为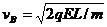

第二次碰后速度再交换。由速度图像也可得到第三次碰前A速度

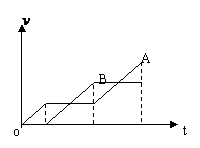
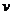
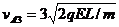　 　　　 (6)　　

此时B的速度为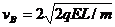 (7)

依此类推第n次碰前A速度为：

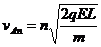　 (8)　　

　 故第n次与第n+1次碰撞经历时间为：

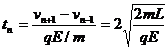　 (9)　

　第n次碰后B以速度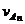匀速运动，

故该时间内A通过的路程为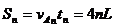：　 (10)　

例4．解析 　粒子进入磁场后做匀速圆周运动，经半周后通过x

轴进入电场后做匀减速直线运动，速度减为零后，又反向匀加

　 速通过x轴进入磁场后又做匀速圆周运动，所以运动有周期性.

它第3次到达x轴时距O点的距离L等于圆半径的4倍(如图

6-13甲所示)

粒子在磁场中做匀速圆周运动的半径为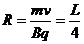　

所以粒子射出时的速度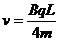　

粒子做圆周运动的半周长为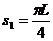　

粒子以速度v进入电场后做匀减速直线运动，能深入的最大距离为y，

因为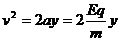

所以粒子在电场中进入一次通过的路程为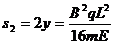　

粒子第1次到达x轴时通过的路程为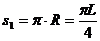　

粒子第2次到达x轴时，已通过的路程为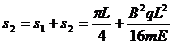　

粒子第3次到达x轴时，已通过的路程为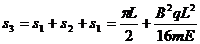　

粒子第4次到达x轴时，已通过的路程为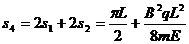　

粒子第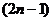次到达x轴时，已通过的路程为　

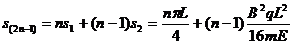
粒子第2n次到达x轴时，已通过的路程为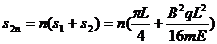　

上面n都取正整数.

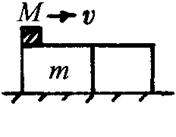
例5．解析　 当铅块向右运动时，铅块与10个相同的扁长木块中的第一块先发生摩擦力，若此摩擦力大于10个扁长木块与地面间的最大静摩擦力，则10个扁长木块开始运动，若此摩擦力小于10个扁长木块与地面间的最大摩擦力，则10个扁长木块先静止不动，随着铅块的运动，总有一个时刻扁长木块要运动，直到铅块与扁长木块相对静止，后又一起匀减速运动到停止.

铅块M在木块上滑行所受到的滑动摩擦力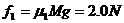

设M可以带动木块的数目为n，则n满足：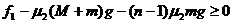

即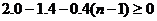

上式中的n只能取整数，所以n只能取2，也就是当M滑行到倒数第二个木块时，剩下的两个木块将开始运动.设铅块刚离开第8个木块时速度为v，则

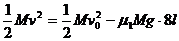
　 得：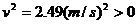

由此可见木块还可以滑到第9个木块上. M在第9个木块

上运动如图6-9甲所示，则对M而言有：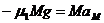

得：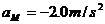

第9及第10个木块的动力学方程为：，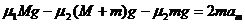

得：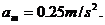

设M刚离开第9个木块上时速度为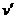，而第10个木块运动的速度为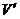，并设木块运动的距离为s，则M运动的距离为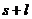，有：

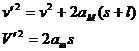
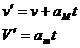
消去s及t求出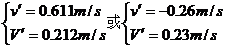：，显然后一解不合理应舍去.

因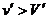，故M将运动到第10个木块上.

再设M运动到第10个木块的边缘时速度为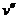，这时木块的速度为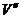，则：

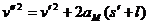
解得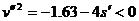：，故M不能滑离第10个木块，只能停在它的表面上，最后和木块一起静止在地面上.

例6．(1)A在盒子内运动时，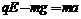　　

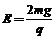
由以上两式得　a＝g　　　　　　　　　

A在盒子内运动的时间　　 A在盒子外运动的时间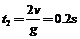

A从第一次进入盒子到第二次进入盒子的时间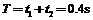　　　　

(2)小球在盒子内运动时，盒子的加速度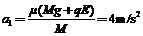　　

小球在盒子外运动时，盒子的加速度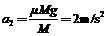

小球运动一个周期盒子减少的速度为　

从小球第一次进入盒子到盒子停下，小球运动的周期数为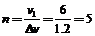

故要保证小球始终不与盒子相碰，盒子上的小孔数至少为2n+1个，即11个．

(3)小球第一次在盒内运动的过程中，盒子前进的距离为

小球第一次从盒子出来时，盒子的速度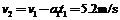

小球第一次在盒外运动的过程中，盒子前进的距离为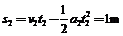

小球第二次进入盒子时，盒子的速度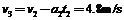

小球第二次在盒子内运动的过程中，盒子前进的距离为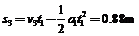

小球第二次从盒子出来时，盒子的速度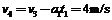

小球第二次在盒外运动的过程中，盒子前进的距离为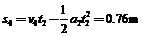　

分析上述各组数据可知，盒子在每个周期内通过的距离为一等差数列，公差d＝0.12m．且当盒子停下时，小球恰要进入盒内，最后0.2s内盒子通过的路程为0.04m．

所以从小球第一次进入盒子至盒子停止运动的过程中，盒子通过的总路程为

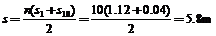
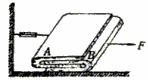
5．如图所示，有两本完全相同的书A、B，书重均为5N，若将两本书等分成若干份后，

交叉地叠放在一起，置于光滑的桌面上，并将书A通过一轻质弹簧秤与墙壁相连，用水平

向右的力F把书B抽出。现测得一组数据如下表：

根据以上数据，试求：

(1)若将书分成32份，弹簧秤的示数为多大？

(2)该书由多少张与首页大小相同的纸组成？

(3)如果两本书任意两张纸之间的动摩擦因数μ都相等，则μ为多大？

4．如图所示，R₁=R₃=R₅=…=R₉₉=5Ω，R₂=R₄=R₆=…=R₉₈=10Ω，R₁₀₀=5Ω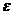，=10V。求：

　 (1)R_AB=？

　 (2)电阻R₂消耗的电功率应等于多少？

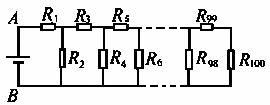　 (3)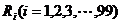消耗的电功率；

　 (4)电路上的总功率.

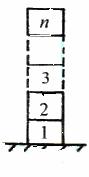
3．有n块质量均为m，厚度为d的相同砖块，平放在水平地面上，现将它们一块一块地叠放起来，如图所示，人至少做多少功？

2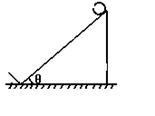．如图所示，一固定的斜面，倾角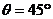，斜面长L=2.00米. 在斜面下端有一与斜面垂直的挡板. 一质量为m的质点，从斜面的最高点沿斜面下滑，初速度为零. 下滑到最底端与挡板发生弹性碰撞(无动能损失). 已知质点与斜面间的动摩擦因数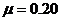，试求此质点从开始到发生第11次碰撞的过程中运动的总路程.

1．(　　 )一物体放在光滑水平面上，初速为零，先对物体施加一向东的恒力F，历时1秒钟，随即把此力改为向西，大小不变，历时1秒钟，接着又把此力改为向东，大小不变，历时1秒钟，如此反复，只改变力的方向，共历时1分钟. 在此1分钟内　　　　　　　　　　　　　

　　 A．物体时而向东运动，时而向西运动，在1分钟末静止于初始位置之东

　　 B．物体时而向东运动，时而向西运动，在1分钟末静止于初始位置

　　 C．物体时而向东运动，时而向西运动，在1分钟末继续向东运动

　　 D．物体一直向东运动，从不向西运动，在1分钟末静止于初始位置之东