
通常情况下,由于物理问题涉及的因素众多、过程复杂,很难直接把握其变化规律进而对其做出准确的判断.但我们若将问题推到极端状态、极端条件或特殊状态下进行分析,却可以很快得出结论.像这样将问题从一般状态推到特殊状态进行分析处理的解题方法就是极端法.极端法在进行某些物理过程的分析时,具有独特作用,恰当应用极端法能提高解题效率,使问题化难为易,化繁为简,思路灵活,判断准确.
用极端法分析问题,关键在于是将问题推向什么极端,采用什么方法处理.具体来说,首先要求待分析的问题有“极端”的存在,然后从极端状态出发,回过头来再去分析待分析问题的变化规律.其实质是将物理过程的变化推到极端,使其变化关系变得明显,以实现对问题的快速判断.通常可采用极端值、极端过程、特殊值、函数求极值等方法.
12.一物体作竖直上抛运动,经过高度为1.8m的窗户历时0.2s,则此物体上升到最高点与窗户上端的距离是多少?(取g=10m/s2)
例题解析:
[例1][解析]由于小球脱离汽球后,先做竖直上抛运动再做自由落体运动,就全过程说是做匀变速直线运动,所以设小球在空中运动的总时间为t,若规定竖直向上的方向为正,则小球的位移s=-120m,v0=10m/s,a=-10m/s2,由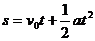 代入数据,解得t=6s。
代入数据,解得t=6s。
[例2][解析]人跌落后在重力作用下做自由落体运动,绳拉直后又受安全带的作用,在重力和弹力共同作用下做变速直线运动,某瞬时速度变为零。
由 得自由落体时间:
得自由落体时间:
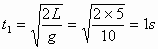
设安全带对工人的平均冲力为F,对人下落的全过程应用动量定理得:
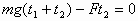
代入数据,解得F=1100N
[例3][解析]解法1:分段列式法.
选物体为研究对象,先研究自由落体过程,只有重力做功,设物体的质量为m,落到沙坑表面时速度为v,根据动能定理有:
mgH=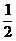 mv2-0 ①
mv2-0 ①
再研究物体在沙坑中的运动过程,重力做正功,阻力Ff做负功,根据动能定理有
mgh-Ff h=0-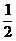 mv2 ②
mv2 ②
由①②两式解得
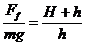
解法2:全程列式法
研究物体运动的全过程,据动能定理有:
mg(H+h)-Ff h=0
解得: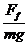 =
=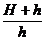
点评:若物体的运动过程包含几个不同的物理过程,用动能定理解题时可以分段列方程,然后联立求解.也可以视全过程为一整体列方程求解.当既能用“分段法”求解,又能用“全程法”求解时,一般来说,全程法比分段法简捷.
[例4][解析]⑴对小球和杆A1组成的系统,由动量守恒定律得:
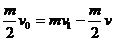 ①
①
又 s=vt ②
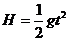 ③
③
①②③三式联立解得: 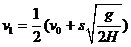 ④
④
回路内感应电动势的最大值 E=BLv1 ⑤
回路内感应电流的最大值 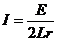 ⑥
⑥
④⑤⑥三式联立解得: 
⑵两棒组成的系统,对它们从开始作用到达到共同速度的全过程由动量守恒定律得:
mv1=2mv2
由能量守恒定律,整个运动过程中感应电流最多产生热量为:
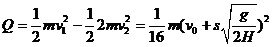
[例5][解析]若依据匀变速运动规律列式,将会出现总时间t比前后两个5秒的和10秒是大还是小的问题:若t>10s将时间分为前5秒和后5秒与中间的时间t2,经复杂运算得t2=-2秒再得出t=8秒的结论。若用逆向的初速度为零的匀加速运动处理,将会简便的多。
视为反向的初速度为零的加速直线运动
则最后5秒通过的路程: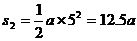
最初5秒通过的路程: 
有题中已知的条件:s1:s2=11:5 得
(10t-25):25=11:25
11. 一个质量为
一个质量为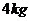 的物体静止在足够大的水平地面上,物体与地面间的动摩擦因数
的物体静止在足够大的水平地面上,物体与地面间的动摩擦因数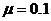 。从
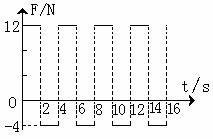
。从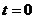 开始,物体受到一个大小和方向呈周期性变化的水平力F作用,力F随时间的变化规律如图所示。求83秒内物体的位移大小和力F对物体所做的功。
开始,物体受到一个大小和方向呈周期性变化的水平力F作用,力F随时间的变化规律如图所示。求83秒内物体的位移大小和力F对物体所做的功。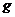 取10m/s2。
取10m/s2。
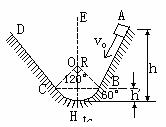
10.如图所示,AB和CD为两个斜面,其上部足够长,下部分别与一光滑圆弧面相切,EH为整个轨道的对称轴,圆弧所对圆心角为120°,半径为2m.某物体在离弧底H高h = 4m处以v0 = 6m / s沿斜面运动,物体与斜面的动摩擦因数μ= 0.04,求物体在AB与CD两斜面上(圆弧除外)运动的总路程(取g = 10m / s2).
9.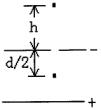 如图是两块水平放置相互平行且正对的金属板,其上板开有一小孔,质量为m,电荷量为q的带正电液滴,自空中自由下落,并由小孔进入匀强电场。设两板电势差为U、距离为d,欲使液滴在板间下落的深度为d/2,则液滴的高度h为多少?
如图是两块水平放置相互平行且正对的金属板,其上板开有一小孔,质量为m,电荷量为q的带正电液滴,自空中自由下落,并由小孔进入匀强电场。设两板电势差为U、距离为d,欲使液滴在板间下落的深度为d/2,则液滴的高度h为多少?
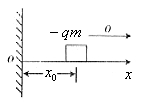
8. 如图所示,一个质量为m,电量为-q的小物体,可在水平轨道x上运动,O端有一与轨道垂直的固定墙,轨道处在场强大小为E,方向沿Ox轴正向的匀强电场中,小物体以初速度v0从x0点沿Ox轨道运动,运动中受到大小不变的摩擦力Ff作用,且Ff<qE,小物体与墙碰撞时不损失机械能,求它在停止前所通过的总路程s。
7.斜面倾角为θ,在斜面底端有一弹性挡板与斜面垂直,在斜面上距离挡板为s0处有一小物块从初速率v0开始沿斜面滑动。若物块与斜面之间的动摩擦因数为µ(µ<tanθ),且滑块每次与挡板碰撞都不改变速率的大小,不考虑物块的大小,求物块总共能运动的路程。
6.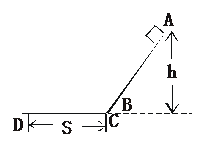 右图中ABCD是一条长轨道,其中AB段是倾角为O的斜面,CD段是水平的,BC是与AB及CD都相切的一小段圆弧,其长度可以不计。一质量为M的小滑块在A点从静止状态释放,沿轨道滑下,最后停在D点。已知A点比CD水平面高出h,CD段的长度为s。现用一沿着轨道方向的力推滑块,使它缓慢地由D点推回到A点时停下。设滑块与轨道间的动摩擦因数为μ,则推力对滑块做的功等于( )
右图中ABCD是一条长轨道,其中AB段是倾角为O的斜面,CD段是水平的,BC是与AB及CD都相切的一小段圆弧,其长度可以不计。一质量为M的小滑块在A点从静止状态释放,沿轨道滑下,最后停在D点。已知A点比CD水平面高出h,CD段的长度为s。现用一沿着轨道方向的力推滑块,使它缓慢地由D点推回到A点时停下。设滑块与轨道间的动摩擦因数为μ,则推力对滑块做的功等于( )
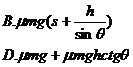
5. 小球A用不可伸长的轻绳系于O点,在O点正下方有一固定的钉子B。开始时,将球A拉到与悬点O同高处无初速释放,若绳长为L,则当B与悬点O的距离d满足什么条件时,球A摆下后将如图所示,绕B点做完整的圆周运动?
小球A用不可伸长的轻绳系于O点,在O点正下方有一固定的钉子B。开始时,将球A拉到与悬点O同高处无初速释放,若绳长为L,则当B与悬点O的距离d满足什么条件时,球A摆下后将如图所示,绕B点做完整的圆周运动?
4.小球由离地面h高处由静止开始下落,落地时与地面碰撞后即以原速率竖直反弹,如果小球运动中所受空气阻力大小恒定为重力的K倍(K<1)则小球第一次反弹的高度为多大?若不计小球的大小,小球总共运动的路程为多大?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com