
2.求函数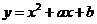 (a、b为常数)的导数.
(a、b为常数)的导数.
分析:根据导数的概念求函数的导数是求导数的基本方法,确定函数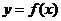 在
在 处的导数有两种方法,应用导数定义法和导函数的函数值法.
处的导数有两种方法,应用导数定义法和导函数的函数值法.
解:1.解法一(导数定义法):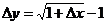 ,
,
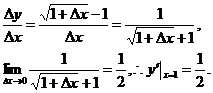
解法二(导函数的函数值法):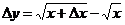 ,
,
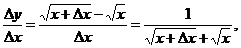
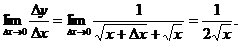
∴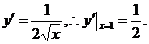
3.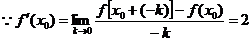 (含
(含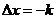 ),
),
∴
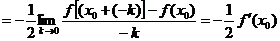
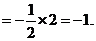 故选A.
故选A.
说明:概念是分析解决问题的重要依据,只有熟练掌握概念的本质属性,把握其内涵与外延,才能灵活地应用概念进行解题,不能准确分析和把握给定的极限式与导数的关系,盲目套用导数的定义是使思维受阻的主要原因.解决这类问题的关键就是等价变形,使问题转化.
利用定义求导数
例 1.求函数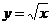 在
在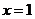 处的导数;
处的导数;
2.原式=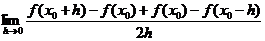
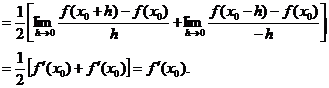
3.若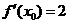 ,则
,则 等于( )
等于( )
A.-1 B.-2 C.-1 D.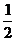
分析:在导数的定义中,增量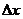 的形式是多种多样的,但不论
的形式是多种多样的,但不论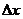 选择哪种形式,
选择哪种形式,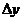 也必须选择相对应的形式.利用函数
也必须选择相对应的形式.利用函数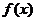 在点
在点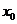 处可导的条件,可以将已给定的极限式班等变形转化为导数定义的结构形式.
处可导的条件,可以将已给定的极限式班等变形转化为导数定义的结构形式.
解:1.原式=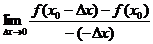
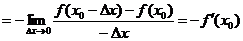
2.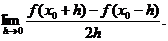
1.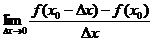 ;
;
16、解析:设冰壶在未被毛刷擦过的冰面上滑行的距离为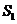 ,所受摩擦力的大小为
,所受摩擦力的大小为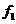 :在 被毛刷擦过的冰面上滑行的距离为
:在 被毛刷擦过的冰面上滑行的距离为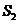 ,所受摩擦力的大小为
,所受摩擦力的大小为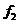 。则有
。则有
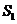 +
+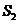 =S ①
=S ①
式中S为投掷线到圆心O的距离。
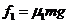 ②
②
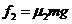 ③
③
设冰壶的初速度为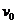 ,由功能关系,得
,由功能关系,得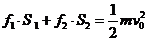 ④
④
联立以上各式,解得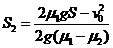 ⑤
⑤
代入数据得
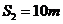 ⑥
⑥
15、解析:设物块到达劈A的低端时,物块和A的的速度大小分别为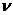 和V,由机械能守恒和动量守恒得
和V,由机械能守恒和动量守恒得
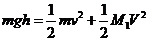 ①
①
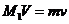 ②
②
设物块在劈B上达到的最大高度为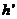 ,此时物块和B的共同速度大小为
,此时物块和B的共同速度大小为 ,由机械能守恒和动量守恒得
,由机械能守恒和动量守恒得
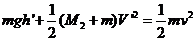 ③
③
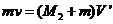 ④
④
联立①②③④式得
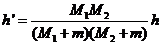 ⑤
⑤
14、解析:⑴设AB碰撞后的速度为v1,AB碰撞过程由动量守恒定律得
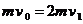
设与C碰撞前瞬间AB的速度为v2,由动能定理得
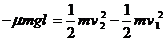
联立以上各式解得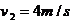
⑵若AB与C发生完全非弹性碰撞,由动量守恒定律得
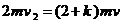
代入数据解得 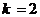
此时AB的运动方向与C相同
若AB与C发生弹性碰撞,由动量守恒和能量守恒得
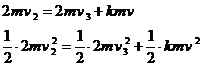
联立以上两式解得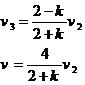
代入数据解得 
此时AB的运动方向与C相反
若AB与C发生碰撞后AB的速度为0,由动量守恒定律得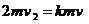
代入数据解得
总上所述得 当 时,AB的运动方向与C相同
时,AB的运动方向与C相同
当 时,AB的速度为0
时,AB的速度为0
当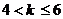 时,AB的运动方向与C相反
时,AB的运动方向与C相反
13、
解析:
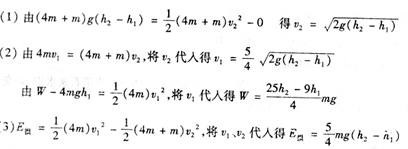
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com